Практическое занятие 2.2. Комбинаторные задачи и их решение.

Вопросы и задания для подготовки к занятию:

18. Численность объединения и пересечения множеств.

19. Правило суммы и правило произведения.

20. Перестановки и вычисление их числа.

21. Размещения вычисление их числа.

22. Сочетания и вычисление их числа.

23. Найти значения выражений:

24. Образуйте из элементов множества 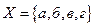все возможные кортежи длины 2, так чтобы в них элементы не повторялись. Как называются эти кортежи в комбинаторике? Сколько их получилось?

25. Сколько трехэлементных подмножеств имеет множество ? Сколько полученных подмножеств: а) содержит элемент 1; б) не содержит элемент 2?

26. На тарелке лежат 8 яблок и 6 груш. Сколькими способами можно выбрать один плод?

27. Решите следующие задачи, используя формулы. Ответ проверь с помощью перебора всех возможных вариантов:

a. Аня, Боря, Вера и Гена – лучшие лыжники школы. На соревно­вания надо выбрать из них троих. Сколькими способами можно это сделать?

b. Государственные флаги некоторых стран состоят из трех горизонтальных полос разного цвета. Сколько различных вариантов фла­гов с белой, синей и красной полосами можно составить?

c. Круг разделили на две части и решили раскрасить их каранда­шами разных цветов. Сколькими способами можно это сделать, если имеются красный, зеленый и синий карандаши?

 

Задания для самостоятельной работы

 

1. На районные соревнования надо выделить от школы одного шахматиста и одну шахматистку. Имеется 7 кандидатур. Сколькими способами можно составить команду?

2. Сколько словарей необходимо переводчику, чтобы он мог переводить непосредственно с любого из четырех языков – русского, английского, немецкого и французского – на любой другой из этих языков?

3. Мальчик выбрал в библиотеке 5 книг. По правилам библиотеки одновременно можно взять только 2 книги. Сколько у мальчика вариантов выбора двух книг из пяти?

4. Школьники из Волгограда собрались на каникулы поехать в Москву, посетив по дороге Нижний Новгород. Из Волгограда в Ниж­ний Новгород можно отправиться на теплоходе или поезде, а из Ниж­него Новгорода в Москву - на самолете, теплоходе или автобусе. Сколькими различными способами могут ребята осуществить свое путешествие? Назовите все возможные варианты этого путешествия.

5. Сколько всевозможных трехзначных чисел можно составить из цифр 1, 2, 3 и 4 так, чтобы цифры в записи числа не повторялись? Изменится ли решение этой задачи, если вместо цифры 4 будет дана цифра 0?

6. Сколько всевозможных четырехзначных чисел можно составить, используя для записи цифры 1, 2, 3 и 4? Какова разность между самым большим и самым маленьким из них?

7. В турнире участвуют 6 человек. Сколькими способами можно распределить между ними места?

8. Сколькими способами можно рассадить 12 человек за круглым столом?

9. Из 20 учащихся класса нужно выбрать старосту, его заместителя и редактора газеты. Сколькими способами это можно сделать?

10. В классе изучаются 7 предметов. В среду 4 урока, причем все разные. Сколькими способами можно составить расписание на среду?

11. Сколько всевозможных трехзначных чисел можно записать, используя цифры 3, 4, 5 и 6 (причем цифры в числе не должны повторяться)?

12. Сколькими способами можно выбрать из 6 человек комиссию, состоящую из трех человек?

13. Сколькими способами можно выбрать 4 краски из 10 различных красок?

14. Сколькими способами можно расставить на полке 3 различные книги? Переставить три различные буквы, три различные цифры?

15. На плоскости отметили 7 точек. Каждые две точки соединили отрезком. Сколько получилось отрезков?

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: