 |
Приведение МДС и тока якоря к обмотке возбуждения
|
|
|
|
Одинаковые по величине МДС якоря и возбуждения создают неодинаковые по величине первые гармоники потоков. Однако характеристика холостого хода, а также нагрузочная характеристика СМ, выражают зависимость потоков и ЭДС от МДС или токов возбуждении. Поэтому при использовании этих характеристик для определения, с учетом насыщения, потоков и ЭДС, создаваемых совместным действием МДС якоря и возбуждения, возникает необходимость в приведении МДС или тока якоря к ОВ.
В процессе приведения определяется МДС или ток возбуждения, эквивалентные по своему действию  или
или  , (
, ( или
или  ).
).
 ;
;
 .
.
В левой части последнего равенства представлена первая гармоника поля, создаваемая МДС продольной реакции якоря  . В правой части – первая гармоника создаваемая эквивалентной МДС возбуждения
. В правой части – первая гармоника создаваемая эквивалентной МДС возбуждения
 .
.
Аналогично
 .
.
Приведенный продольный и поперечный ток возбуждения
 ,
,
 .
.
В случае неявнополюсной СМ
 ,
,
 .
.
При анализе работе СМ широко используется представление электромагнитных величин в относительных единицах. При этом в качестве базовых величин напряжения, тока, сопротивления, индуктивности принимают их номинальные значения  .
.
Следовательно, электромагнитные величины в относительных единицах будут
 .
.
Мгновенные значения напряжения и тока обычно выражают в долях от их максимальных значений:
 .
.
За базовую величину тока возбуждения принимаются ток возбуждения, создающий в воздушном зазоре такую же первую гармонику поля, что и номинальный ток якоря по продольной оси. Нередко за базовый принимается ток возбуждения соответствующий номинальному напряжению холостого хода.
Векторные диаграммы трехфазных синхронного
Генератора при симметричной нагрузке
|
|
|
Основные виды векторных диаграмм напряжения
Синхронного генератора
а) Явнополюсная СМ
Фазное напряжение СГ
 . (3.1)
. (3.1)
Здесь  – ЭДС, индуктируемое в обмотке якоря потоком возбуждения,
– ЭДС, индуктируемое в обмотке якоря потоком возбуждения,
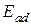 и
и  – ЭДС продольной и поперечной реакции якоря,
– ЭДС продольной и поперечной реакции якоря,
 – ЭДС рассеяния,
– ЭДС рассеяния,
 – падение напряжения в обмотке якоря.
– падение напряжения в обмотке якоря.
Перепишем уравнение (3.1) в виде
 (3.1,а)
(3.1,а)
или
 . (3.2)
. (3.2)
Согласно (3.1,а) фазное напряжение синхронного генератора ( СГ) равно ЭДС возбуждения минус падения напряжения на индуктивных сопротивлениях реакции якоря и на активном сопротивлении цепи якоря. Или согласно (3.2) ЭДС возбуждения равно напряжению на зажимах СГ плюс падения напряжения на индуктивных и активных сопротивлениях. Из предыдущего известно
 ,
,
где  – результирующая ЭДС, создаваемая результирующим потоком воздушного зазора
– результирующая ЭДС, создаваемая результирующим потоком воздушного зазора  . В результате уравнение (3.1,а) можно переписать следующим образом
. В результате уравнение (3.1,а) можно переписать следующим образом
 .
.
Построим векторную диаграмму СГ при активно-индуктивной и активно-емкостной нагрузках (рис. 3.11). Как следует из построения, при одном и том же возбуждении напряжение на зажимах СГ в случае активно-индуктивной нагрузке получается меньшее, чем напряжение при активно-емкостной. В первом случае (рис. 3.11,а) реакция якоря – размагничивающая, а во втором случае
(рис. 3.11,б) – намагничивающая. Угол θ называют углом нагрузки. Будем считать, что генератор, у которого напряжение отстает от ЭДС, угол θ положительный.
Эти векторные диаграммы называют диаграммами Блонделя.
 .
.
Данная векторная диаграмма может быть видоизменена. Для этого воспользуемся разложением ЭДС рассеяния на две составляющие:
 ,
,
тогда  ,
,
или  , (3.3)
, (3.3)
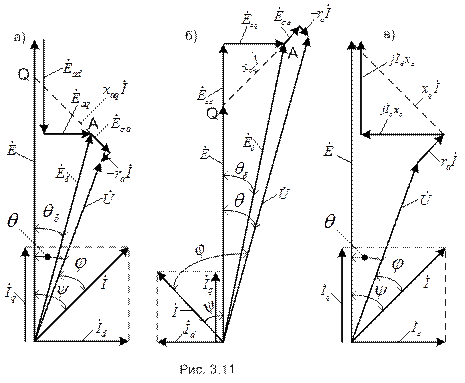
где  и
и  – синхронные индуктивные сопротивления по продольной и поперечной осям.
– синхронные индуктивные сопротивления по продольной и поперечной осям.
Видоизмененная векторная диаграмма Блонделя для случая активно–индуктивной нагрузки в соответствии с (3) имеет вид (рис. 3.11,в).
б) Неявнополюсная СМ
|
|
|

 ,
,
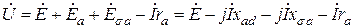 , (3.4)
, (3.4)
 .
.
Не видоизмененная и видоизмененная векторная диаграмма имеет вид (рис. 3.12).
|
|
|


