 |
Построение векторной диаграммы СМ с учетом насыщения
|
|
|
|
Рассмотренные выше векторные диаграммысправедливы для любого установившегося режима, если при их построении использовать хad, хaq, хd, хq, соответствующие реальному насыщению магнитной цепи в рассматриваемом режиме. Представляет интерес построение векторной диаграммы с учетом конкретного насыщения магнитной цепи в заданном режиме, что позволяет определить МДС возбуждения в этом режиме.
а) Неявнополюсная СМ
При построении векторной диаграммыс учетом насыщения в данном случае удобно использовать диаграмму Потье (рис. 3.13). При этом должно быть задано 
. Кроме того, предполагается заданной характеристика холостого хода (х.х.х).
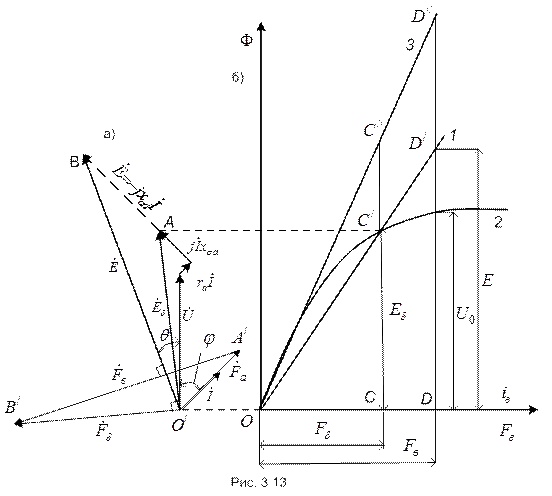
По данным величинам строится вектор результирующей ЭДС 
, соответствующей результирующему потоку воздушного зазора, то есть 
. ЭДС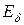 
определяет реальное насыщение магнитной цепи в заданном режиме. По этой величине 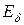на характеристике холостого хода (рис. 3.13,б, кривая 2) определяется рабочая точка 
и соответствующая ей результирующая МДС 
, (
). Но известно, что 
, где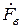 
– МДС обмотки возбуждения (ОВ), а 
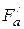- МДС реакции якоря, приведенная к обмотке возбуждения. Отсюда 
. Представим это уравнение графически (см. рис. 3.13,а), учитывая, что опережает 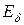на 90о. В результате построения получаем диаграмму Потье (рис. 3.13), представляющую собой совмещение диаграмм МДС и ЭДС.
Зная вектор 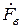по величине и направлению, можно определить направление вектора 
. Величина вектора определяется точкой пересечения продолжения вектора 
с вектором (точка В). Далее легко доказать, что величина насыщенного значения Е соответствует отрезку 
. С этой целью следует построить спрямленную насыщенную характеристику 1, проведя ее через точки О и . Непосредственно из векторной диаграммы (рис. 3.13,а) следует, что
|
|
|
.
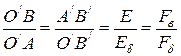С другой стороны согласно (рис. 3.13,б)
,
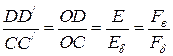т. е. 
. Прямая 3 – касательная к начальному участку характеристике холостого хода, представляет собой ненасыщенную спрямленную характеристику холостого хода. По ней можно определить ненасыщенные значения ЭДС возбуждения и значения 
и 
(результирующие ЭДС).
; 
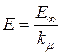, где 
.
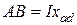, следовательно, 
.
б) Явнополюсная СМ
При этом должно быть заданы , коэффициент насыщения по поперечной оси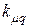 
. Кроме того, предполагается заданной характеристика холостого хода (х.х.х.).
На первом этапе строится вектор результирующей ЭДС 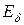(рис. 3.14). Будем считать, что 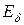определяет насыщение магнитной цепи в рассматриваемом режиме. Прямая 
– насыщенная спрямленная характеристика для этого режима. Далее следует определить величину 
.
.
Отношение 
можно определить по ненасыщенной характеристике холостого хода (рис. 3.14, прямая 3). При этом учитывается, что соответствующая приведенная МДС якоря равна 
. На продолжении вектора зафиксируем точку Q, лежащую на направлении вектора . С этой целью на указанном продолжении () откладывается отрезок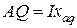 
. Зная направление можно определить 
, а также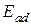 
, определяющую точное насыщение машины по продольной оси. При этом так же определяется вектор 
по величине и направлению. Далее следует определить величину вектора 
и величину насыщенного значения ЭДС . Это осуществляется следующим способом
,
Ненасыщенное значение индуктивного сопротивления по продольной оси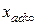 
можно определить расчетным путем, как это делалось выше.
. Отложив вектор определяют вектор .
Характеристики синхронного генератора
Общие замечания
Основными характеристиками СГ являются: характеристика холостого хода (х.х.х.), характеристика короткого замыкания (х.к.з.), внешняя, регулировочная, индукционная–нагрузочная характеристики.
|
|
|
Эти характеристики можно построить по расчетным данным с использованием векторных диаграмм, а также построить и по опытным данным. Изобразим одну из опытных схем для снятия характеристик с СГ
(рис. 3.15). Нагрузка СГ осуществляется с помощью регулирования сопротивлений 
, представляющих собой параллельное соединение трехфазного реостата и трехфазной индукционной катушки. Активная мощность СГ изменяется с помощью первичного двигателя.
|
|
|
