 |
Расчет дисперсии по формуле по индивидуальным данным
|
|
|
|
Техника вычисления дисперсии сложна, а при больших значениях вариантов и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.
Дисперсия имеет следующие свойства.
1. Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсию не изменяет.
2. Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсию не изменяет.
3. Уменьшение или увеличение каждого значения признака в какое-то число раз k соответственно уменьшает или увеличивает дисперсию в k 2 раз, а среднее квадратическое отклонение ¾ в k раз.
4. Дисперсия признака относительно произвольной величины 
всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величинами:
Если А = 0, то приходим к следующему равенству:
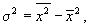
т. е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.
Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.
Порядок расчета дисперсии простой:
1) определяют среднюю арифметическую:
2) возводят в квадрат среднюю арифметическую:
3) возводят в квадрат отклонение каждого варианта ряда:
хi 2.
4) находят сумму квадратов вариантов:
5) делят сумму квадратов вариантов на их число, т. е. определяют средний квадрат:
6) определяют разность между средним квадратом признака и квадратом средней:
Рекомендация:
Обратитесь к примерам по указанным ссылкам: пример 6.3.1.
Рассмотрим расчет дисперсии в интервальном ряду распределения.
Порядок расчета дисперсии взвешенной (по формуле 
) следующий:
|
|
|
1) определяют среднюю арифметическую:
2) возводят в квадрат полученную среднюю:
3) возводят в квадрат каждый вариант ряда:
4) умножают квадраты вариантов на частоты:
5) суммируют полученные произведения:
6) делят полученную сумму на сумму весов и получают средний квадрат признака:
7) определяют разность между средним значением квадратов и квадратом средней арифметической, т. е. дисперсию:
Рекомендация:
Обратитесь к примерам по указанным ссылкам: пример 6.3.2.
Средняя величина отражает тенденцию развития, т. е. действие главных причин. Среднее квадратическое отклонение измеряет силу воздействия прочих факторов.
Показатели относительного рассеивания
Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Показатель меры относительного рассеивания рассчитывается как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.
1. Коэффициент осцилляции (К о) отражает относительную колеблемость крайних значений признака вокруг средней:
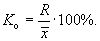
2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:
3. Коэффициент вариации (V):
.
Поскольку среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин. Исходят из того, что если V больше 40%, то это говорит о большой колеблемости признака в изучаемой совокупности.
|
|
|
|
|
|
