 |
Классификация статистических графиков
|
|
|
|
При всем своем многообразии статистические графики в курсе «Статистика» классифицируются по ряду признаков: способу построения, форме применяемых графических образов, характеру решаемых задач.
По способу построения статистические графики подразделяются на диаграммы, картограммы и картодиаграммы.
Диаграмма представляет собой чертеж, на котором статистическая информация изображается посредством геометрических фигур или символических знаков.
Диаграмма сравнения показывает соотношение признака статистической совокупности.
На рис. 7.1 отображены доли иностранных инвестиций в экономику России на 1 января 2005 г. График отчетливо показывает страны с наибольшими (Германия, Кипр, Великобритания) и наименьшими (Италия, Финляндия) долями инвестиций.
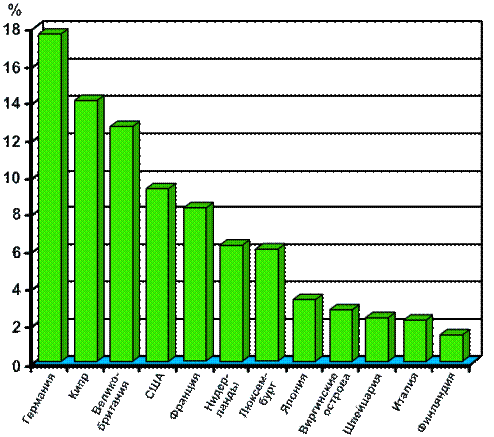
Рис. 7.1. Столбиковая диаграмма сравнения
Каждое значение изучаемого показателя изображается в виде вертикального столбика. Количество столбиков определяется числом изучаемых показателей (данных). Расстояние между столбиками должно быть одинаковым. У основания столбиков дается название изучаемого показателя.
В этих диаграммах основания столбиков располагаются вертикально. Должна быть одинаковая ширина полос.
Эту же диаграмму можем построить иначе: с помощью полосовой диаграммы (рис. 7.2).
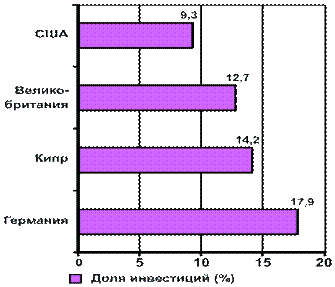 |
Рис. 7.2. Полосовая диаграмма сравнения
При построении столбиковых диаграмм используется, как и в линейных графиках, прямоугольная система координат.
По оси абсцисс размещается основание столбиков. Их ширина может быть произвольной, но обязательно одинаковой для каждого столбика.
Основные требования построения данных диаграмм:
■ соответствие столбиков по высоте, а полос ¾ по длине, отображаемым цифрам;
|
|
|
■ недопустимость разрывов масштабной шкалы и начала ее не от нулевой отметки.
Структурная диаграмма позволяет сопоставить статистические совокупности по составу (рис. 7.3).
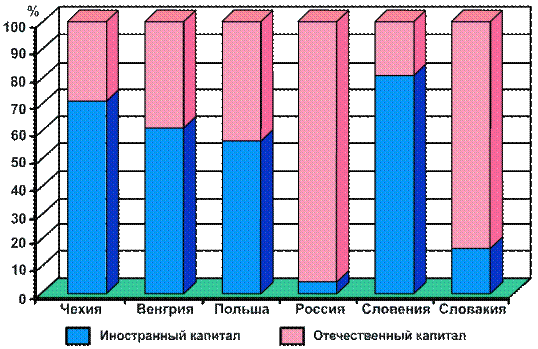
Рис. 7.3. Структурно-столбиковая диаграмма,
характеризующая структуру капитала стран
Центральной и Восточной Европы на 1 января 2005 г.
Секторная диаграмма строится таким образом, чтобы каждый сектор занимал площадь круга пропорционально удельному весу отображаемых частей целого (рис. 7.4). Затем необходимо найти значения центральных углов (1% = 3,6 градуса).
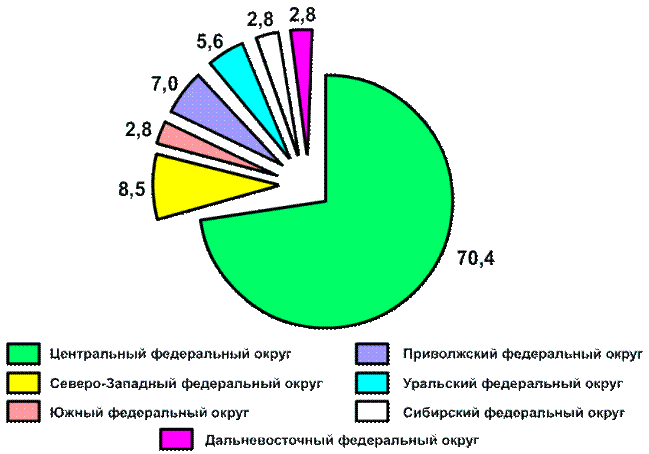
Рис. 7.4. Структурно-секторная диаграмма.
Объем иностранных инвестиций, привлеченный
различными округами Российской Федерации на 1 января 2005 г.
Рекомендация:
Обратитесь к примерам по указанным ссылкам: пример 7.3.1.
При изучении статистической информации о социально-экономических процессах и явлениях применяются так называемые радиальные диаграммы. Строятся они на базе полярных координат. Началом отсчета в них служит центр окружности, а носителем масштабных шкал являются радиусы круга. Обычно в основе радиальных диаграмм лежат повторяющиеся годовые циклы с помесячными или поквартальными данными. Так, при изучении годового цикла с помесячными данными окружность делят радиусами на 12 равных частей. Каждому радиусу дается название месяца года, а их расположение подобно циферблату часов. На каждом радиусе в соответствии с установленным масштабом наносятся точки, соответствующие изучаемым за каждый месяц данным. Полученные таким образом точки соединяются между собой линиями. В результате получается спиралеобразная линия, характеризующая внутригодовые циклы коммерческой деятельности.
Диаграмма динамики показывает изменение явления во времени. Такая диаграмма может быть изображена с помощью уже рассмотренных типов диаграмм.
|
|
|
Диаграмма связи показывает функциональную зависимость одного признака от другого ¾ обычный график на координатной сетке: y = f (x) (рис. 7.5).
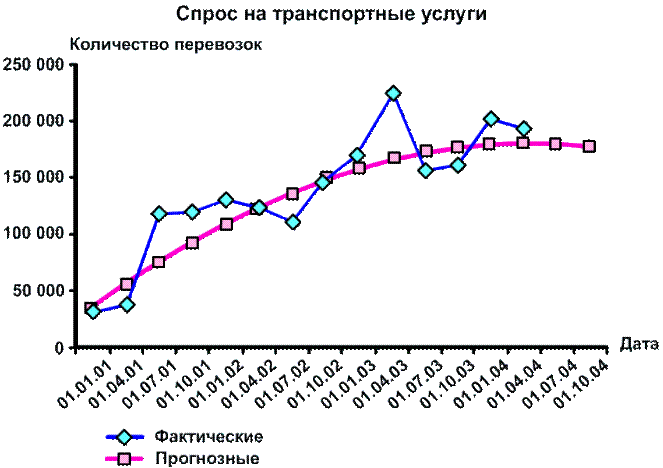
Рис. 7.5. Динамика грузоперевозок в Российской Федерации
за период 2001-2004 гг.
Статистическая карта ¾ вид графика, который иллюстрирует содержание статистических таблиц, где подлежащим является административное или географическое деление совокупности. На лист изображения наносится контурная географическая карта, отражающая деление совокупности на группы. Статистическая карта называется картограммой, вся информация на ней отображается в виде штриховки, линий, точек, окраски, отражающих изменение какого-либо показателя.
На картодиаграмме на фоне карты присутствуют элементы диаграммных фигур. Преимущество картодиаграммы перед диаграммой состоит в том, что она не только дает представление о величине изучаемого показателя на различных территориях, но и изображает пространственное размещение изучаемого показателя.
В зависимости от формы применяемых графических образов статистические графики могут быть точечными, линейными, плоскостными и фигурными.
В точечных графиках в качестве графических образов применяется совокупность точек.
В линейных графиках графическими образами являются линии.
Плоскостные графики изображают на трехмерной плоскости.
Для фигурных графиков графическими образами служат геометрические фигуры: прямоугольники, квадраты, окружности.
При обработке и отображении экспериментальных данных, в которых изучаемый признак может принимать любое значение из некоторого интервала, используют следующие способы представления данных:
■ гистограмма;
■ полигон частот;
■ полигон накопленных частот (кумулята).
Гистограмма состоит из примыкающих друг к другу прямоугольников, изображенных на координатной сетке.
При построении гистограмм могут возникнуть следующие случаи.
1. Равные интервалы группировки данных.
Рассмотрим на примере.
Имеются данные о группировке рабочих по стажу лет, (табл. 7.1).
Таблица 7.1
Группы рабочих по стажу
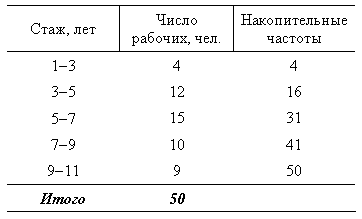
Построим гистограмму (рис. 7.6).
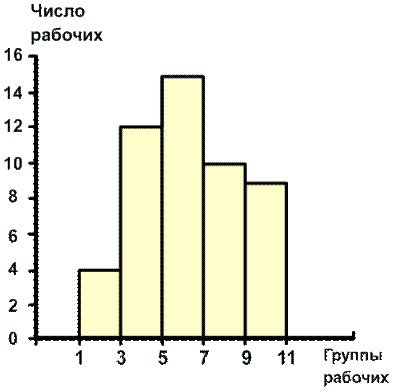
Рис. 7.6. Распределение рабочих по стажу лет
На рисунке откладываются прямоугольники с высотой, прямо пропорциональной частоте данного интервала.
|
|
|
Наибольшее число рабочих имеют стаж работы от 5 до 7 лет.
2. Открытые крайние интервалы группировки.
Предположим, что первый и последний интервалы открытые. В таких случаях используется стандартный прием. Условно ширина первого открытого интервала принимается равной ширине следующего интервала. Ширина последнего принимается равной ширине предыдущего (табл. 7.2).
Таблица 7.2
Группы рабочих по стажу

В данном случае гистограмма будет такой же, как на рис. 7.7.
3. Неравные интервалы группировки.
Предположим, что вместо двух интервалов (3-5 и 5-7) имеется один. Интервал стал шире в 2 раза, а высота стала не 27, а 13,5, с тем, чтобы площадь прямоугольника не менялась. Высоту прямоугольника можно определить по формуле:
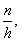
где n ¾ частоты попадания (27);
h ¾ количество интервалов (2).
Полигон частот ¾ ломаная линия, соединяющая точки, соответствующие срединным значениям интервалов группировки и частотам интервалов.
Полигон частот получается из гистограммы, если соединить середины вершин прямоугольников ломаной линией.
Полигон накопительных частот. В данном случае для построения используются накопленные частоты. Построим полигон (рис. 7.7).

Рис. 7.7. Распределение рабочих по стажу лет
|
|
|


