 |
Метод аналитического выравнивания
|
|
|
|
Рассмотрим применение метода аналитического выравнивания по прямой для выражения основной тенденции на примере.
Рекомендация:
Обратитесь к примерам по указанным ссылкам: пример 8.4.1.
Уравнение прямой при аналитическом выравнивании ряда динамики имеет следующий вид:

где  ¾выровненный (средний) уровень динамического ряда;
¾выровненный (средний) уровень динамического ряда;
a 0, a 1 ¾ параметры искомой прямой;
t ¾ условное обозначение времени.
Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров a 0 и a 1:

где у ¾ исходный уровень ряда динамики;
n ¾ число членов ряда.
Система уравнений упрощается, если значения t подобрать так, чтобы их сумма равнялась нулю, т. е. начало времени перенести в середину рассматриваемого периода.
Если  то
то

Исследование динамики социально-экономических явлений и установление основной тенденции развития дают основание для прогнозирования (экстраполяции) ¾ определения будущих размеров уровня экономического явления. Используют следующие методы экстраполяции:
■ средний абсолютный прирост;
■ средний темп роста;
■ экстраполяцию на основе выравнивания по какой-либо аналитической формуле.
Расчет индекса сезонности
Покажем расчет индекса сезонности на примере.
Рекомендация:
Обратитесь к примерам по указанным ссылкам: пример 8.5.1.
Для ряда внутригодовой динамики, в которой основная тенденция роста незначительна, изучение сезонности основано на методе постоянной средней, являющейся средней из всех рассматриваемых уровней. Самый простой способ заключается в следующем: для каждого года рассчитывается средний уровень, а затем с ним сопоставляется (в процентах) уровень каждого месяца.
|
|
|
Однако помесячные данные одного года из-за элемента случайности могут быть ненадежными для выявления закономерности колебаний. Поэтому на практике используются помесячные данные за ряд лет (обычно не менее трех лет). Тогда для каждого месяца рассчитывается средняя величина уровня за три года, затем определяются среднемесячный уровень для всего ряда и отношение средних для каждого месяца к общему среднемесячному уровню ряда (в процентах).
Глава 9. Индексный метод и его применение в анализе социально-экономических явлений
Перед изучением данной главы внимательно прослушайте введение к главе. Затем изучите последовательно материалы параграфов главы, обращаясь по мере необходимости к объектам «Видеоматериалы», «Глоссарий», «Персоналии», «Примеры». После изучения каждого параграфа рекомендуется выполнить тренировочные задания.
Особое внимание при изучении главы обратите на содержание видеолекции «Индексный метод и его применение в анализе социально-экономических явлений». После изучения всех параграфов прослушайте основные выводы по главе. Затем проверьте свои знания по главе, выполнив контрольные задания и решив контрольные задачи и упражнения, приведенные ниже.
Задачи и упражнения
9.1. Имеются следующие данные о реализации мясных продуктов на городском рынке:

Рассчитайте сводные индексы цен, физический объем реализации, товарооборота, а также абсолютную величину перерасхода покупателей от роста цен.
9.2. Деятельность торговой фирмы за два месяца 2003 г. характеризуется следующими данными:

Оцените общее изменение физического объема реализации с учетом того, что в апреле фирма повысила все цены на 8%.
9.3. Розничный товарооборот региона в январе 2003 г. характеризуется следующими данными:

Определите сводный индекс цен на потребительские товары.
|
|
|
9.4. Индекс переменного состава ¾ 120%. Под влиянием структурных сдвигов произошло увеличение на 5%. Чему равен индекс, характеризующий изменение средней величины без учета влияния структурных сдвигов?
9.5. Цены на продукцию возросли на 15%, товарооборот ¾ на 10%. Определите изменение физического объема.
9.6. Имеются следующие данные о динамике потребления за два полугодия:

Определите общее изменение потребительских цен по всем товарным группам.
9.7. Строительно-производственная деятельность двух предприятий города характеризуется следующими данными:

Определите:
1) на сколько процентов изменилась средняя цена 1 м2 жилья в отчетном году по сравнению с базисным;
2) на сколько долларов изменилась средняя цена 1 м2 жилья под влиянием ее изменения на каждом предприятии;
3) на сколько процентов изменилась средняя цена 1 м2 жилья под влиянием структурных сдвигов;
4) на сколько тыс. дол. изменилась стоимость вводимого жилья под влиянием изменения средней цены.
Проанализируйте результаты и сделайте выводы.
Понятие индексов. Их виды
Индексы ¾ важнейший обобщающий показатель. С их помощью можно измерить динамику социально-экономического явления за два или более периодов времени, динамику среднего показателя и сопоставить уровни явления в пространстве, по странам, экономическим районам, областям и т. д. Индексы используются для определения степени влияния изменений значений одних показателей на динамику других, а также для пересчета значений макроэкономических показателей из фактических цен в сопоставимые.
Простейший показатель, применяемый в индексном анализе, ¾ индивидуальный индекс, который характеризует изменение во времени или в пространстве отдельных однородных элементов совокупности. Например, индивидуальные индексы физического объема продукции, цен, себестоимости единицы продукции.
В экономических расчетах чаще всего используются сводные, или общие, индексы, которые характеризуют изменение совокупности в целом.
Построение этих индексов является содержанием индексной методологии, в которой сложились две концепции: синтетическая и аналитическая.
Согласно синтетической концепции особенность общих индексов состоит в том, что они выражают относительное изменение сложных явлений, отдельные части которых непосредственно несоизмеримы, и поэтому индексы ¾ показатели синтетические.
|
|
|
В соответствии с аналитической концепцией индексы трактуются как показатели, необходимые для измерения влияния изменения составных частей, факторов сложного явления на изменение уровня этого явления. Поэтому индексной методологией предусматривается определение влияния каждого из факторов путем элиминирования влияния других факторов на уровень изучаемого явления. Такие индексы ¾ показатели аналитические.
Общие индексы строят для количественных и качественных показателей. В зависимости от цели исследования и наличия исходных данных используют различные формы построения общих индексов: агрегатную или средневзвешенную.
При построении агрегатного индекса необходимо решить проблему выбора весов, при этом руководствуются следующим правилом: если строится индекс количественного показателя, то веса берутся за базисный период; если строится индекс качественного показателя, то используются веса отчетного периода.
В статистической практике, помимо агрегатных, применяются средневзвешенные индексы: среднеарифметический и среднегармонический.
Индексный метод служит также для изучения динамики средних величин и выявления факторов, влияющих на динамику средних. С этой целью исчисляется система взаимосвязанных индексов: переменного, постоянного состава и структурных сдвигов.
Индекс переменного состава представляет собой отношение двух взвешенных средних величин с переменными весами, характеризующими изменение индексируемого (осредняемого) показателя.
Индекс переменного состава (I пер.с) для качественных показателей имеет следующий вид:

Величина этого индекса характеризует изменения средневзвешенной средней за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.
Индекс постоянного состава (I п.с) учитывает изменения только индексируемой величины, показывает средний размер изменения изучаемого показателя у единиц совокупности и выглядит следующим образом:
|
|
|

Для расчета индекса постоянного состава можно использовать агрегатную форму индекса:

Индекс структурных сдвигов (I стр.сдв) характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя и рассчитывается по формуле:

Под структурными изменениями понимается изменение доли отдельных групп единиц совокупности в общей их численности (d).
В индексах средних уровней в качестве весов могут быть взяты удельные веса единиц совокупности  Тогда систему индексов можно записать в таком виде:
Тогда систему индексов можно записать в таком виде:

Система взаимосвязанных индексов имеет следующий вид:
I пер.с = I п.с × I стр.сдв.
При изучении динамики социально-экономических явлений за некоторый интервал времени, включающий в себя более двух периодов времени, используется система индексов: цепные индексы с переменными весами; цепные индексы с постоянными весами, базисные индексы с переменными весами, базисные индексы с постоянными весами.
Для сравнения (сопоставления) показателей в пространстве (по странам, экономическим районам, областям и т. п.) применяются территориальные индексы.
В рыночной экономике особую роль играют индексы цен, которые позволяют оценить динамику цен на товары, измерить инфляцию при макроэкономических исследованиях, пересчитать важнейшие стоимостные показатели системы национальных счетов (СНС) из фактических цен в сопоставимые и др. Для решения различных задач могут быть использованы индексы цен Г. Пааше и Э. Ласпейреса. Весами в индексе Г. Пааше выступает количество продукции текущего периода, а в индексе цен Э. Ласпейреса ¾ количество продукции базисного периода.
Средняя геометрическая из произведения двух агрегатных индексов цен Э. Ласпейреса и Г. Пааше представляет собой индекс цен И. Фишера.
Пересчет в основных стоимостных показателях СНС из фактических цен в сопоставимые осуществляется с помощью индекса-дефлятора. В основе расчета индекса-дефлятора лежит формула Г. Пааше ¾ агрегатная формула с текущими весами.
Расчет сводного индекса
Рассмотрим методику расчета сводных индексов на конкретном примере.
Рекомендация:
Обратитесь к примерам по указанным ссылкам: пример 9.2.1.
Цены разных товаров, реализуемых в розничной торговле, складывать неправомерно, однако с экономической точки зрения допустимо суммировать их товарооборот. Если сравнивать товарооборот в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота:
|
|
|
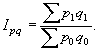
Рассчитаем индекс товарооборота для примера 1:

Мы получим, что товарооборот в целом по рассматриваемой товарной группе в текущем периоде по сравнению с базисным уменьшился на 0,9% (100-99,1).
На величину данного индекса оказывает влияние как изменение цен на товары, так и изменение объемов их реализации. Для того чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких качественных показателей, как цена, себестоимость, производительность труда, количественный показатель обычно фиксируют на уровне текущего уровня. Таким способом получают сводный индекс цен:

Числитель данного индекса содержит фактический товарооборот текущего периода. Знаменатель же представляет собой условную величину, показывающую, каким был бы товарооборот в текущем периоде при условии сохранения цен на базисном уровне. Поэтому соотношение этих двух категорий и отражает изменение цен. Изменение же количества реализованной продукции не влияет на величину индекса.
Вычислим сводный индекс цен для примера 1:

Следовательно, по данной товарной группе цены в октябре по сравнению с августом снизились на 31,7%.
Числитель и знаменатель сводного индекса цен можно интерпретировать с точки зрения потребителей. Числитель представляет собой сумму денег, фактически уплаченных покупателями за приобретенные в текущем периоде товары. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились. Разность числителя и знаменателя будет отражать величину экономии (если знак «-») или перерасхода (если знак «+») покупателей от изменения цен:

Третьим индексом в данной индексной системе является сводный индекс физического объема реализации. Он характеризует изменение количества проданных товаров не в денежных, а в физических единицах измерения:

Весами в данном индексе выступают цены, которые фиксируются на базисном уровне.
Индекс физического объема реализации в примере 1 составит:

Физический объем реализации в октябре по сравнению с августом увеличился в 1,45 раза, или на 51 500 руб. (165 500 - 114 000).
Между рассчитанными индексами существует следующая взаимосвязь:
Ip × Iq = Ipq.
Используя взаимосвязь индексов, проверим правильность вычислений в примере 1:
Ipq = Ip × Iq = 0,683 × 1,452 = 0,991, или 99,1%.
Следовательно, снижение товарооборота (на 0,9%) обусловлено ростом объема проданной продукции (на 45,2%) и снижением цен (на 68,3%), что в абсолютном выражении составило -1000 руб. (-52 500 + 51 500).
Мы рассмотрели применение агрегатных индексов в анализе товарооборота цен и физического объема реализации. При анализе результатов производственной деятельности промышленного предприятия приведенные сводные индексы соответственно называются индексом стоимости продукции, индексом оптовых цен и индексом физического объема продукции.
|
|
|


