 |
Прогнозирование с помощью методов экстраполяции
|
|
|
|
| 1. Установление цели и задачи исследования, анализ объекта прогнозирования | |
| 2. Подготовка исходных данных | |
| 3. Фильтрация исходного временного ряда | |
| 4. Логический отбор видов аппроксимирующей функции | |
| 5. Оценка математической модели прогнозирования | |
| 6. Выбор математической модели прогнозирования |
Прогнозирование с помощью методов экстраполяции должно включать в себя следующие этапы работ:
1.Установление цели и задачи исследования, анализ объекта прогнозирования
Прогнозирование развития любой системы (предприятия, фирмы и т.д.) предъявляет специфические требования к параметрам (объектам), характеризующим и определяющим ее развитие. Поэтому необходимо на первом этапе работ провести детальное логическое изучение системы: зависимости рассматриваемого объекта (параметра, показателя) от других систем одного уровня и субсистемы (системы более высшего уровня); взаимосвязи между данным объектом и другими объектами системы; установления характера предоставления статистических данных об объекте.
2. Подготовка исходных данных
Работы по этому этапу начинаются с проверки временного ряда, в результате которой устанавливаются полнота ряда (наличие данных за каждый год (месяц, квартал) ретроспективного периода), сопоставимость данных и в случае необходимости проверка методики приведения данных к сопоставимому виду. Если временной ряд представлен не полностью, то необходимо недостающие данные определить с помощью тех или иных методов интерполяции в зависимости от характера протекания процесса.
Наряду с этим осуществляется также формирование массива функций, который в последующем будет использован для выбора вида математической модели.
|
|
|
3. Фильтрация исходного временного ряда
В результате этой процедуры устраняются случайные возмущения (флуктуации), возникающие в результате воздействия неучтенных факторов или ошибок измерения относительно наиболее вероятного протекания процесса, и, тем самым, исключается искажающее влияние случайных колебаний на выбор вида регрессии. Фильтрация исходного динамического ряда включает в себя его сглаживание и выравнивание.
Сглаживание применяется для устранения случайных отклонений (шума) из экспериментальных значений исходного ряда. Сглаживание производится с помощью многочленов, приближающих (обычно по методу наименьших квадратов) группы опытных точек. Наилучшее сглаживание получается для средних точек группы, поэтому желательно выбирать нечетное количество точек в сглаживаемой группе. Обычно их выбирают 3 или 5. Например, по первым трем точкам ( ) сглаживают среднюю
) сглаживают среднюю  , затем по следующей тройке (
, затем по следующей тройке ( ) сглаживают
) сглаживают  и т.д. Крайние точки сглаживают по специальным формулам.
и т.д. Крайние точки сглаживают по специальным формулам.
Чаще всего для сглаживания применяют линейную зависимость. Тогда формулы сглаживания для групп из трех точек имеют вид:
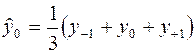 ; (1)
; (1)
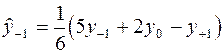 ; (2)
; (2)
 ; (3)
; (3)
где  - значения исходной и сглаженной функции в средней точке группы;
- значения исходной и сглаженной функции в средней точке группы;
 - значение исходной и сглаженной функции в левой точке группы;
- значение исходной и сглаженной функции в левой точке группы;
 - значения исходной и сглаженной функции в правой точке группы.
- значения исходной и сглаженной функции в правой точке группы.
Формулы (2), (3) применяются для сглаживания крайних точек ряда. Для сглаживания по 5 точкам формулы имеют вид:
 ; (4)
; (4)
 (5)
(5)
 ; (6)
; (6)
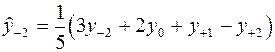 ; (7)
; (7)
 . (8)
. (8)
Cглаживание (даже в простом линейном варианте) является во многих случаях эффективным средством выявления тренда при наличии в экспериментальных точках случайных помех и ошибок измерения.
Выравнивание применяется для более удобного представления исходного ряда без изменения его числовых значений. Выравниванием называется приведение исходной эмпирической формулы
|
|
|
 , (9)
, (9)
где  - время,
- время,  - параметры
- параметры
к виду: 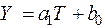 . (10)
. (10)
Использование двухпараметрической зависимости (9) объясняется ее наибольшим распространением в практике прогнозирования и сравнительно простыми способами получения выравниваемых формул. Функции с большим (чем 2) числом параметров выравниваются не всегда, и формулы имеют громоздкий вид.
Наиболее распространенными способами выравнивания являются логарифмирование и замена переменных.
Пример 1. Исходная функция 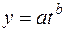 .
.
Логарифмируя, получим  .
.
Вводя замену переменных, имеем:
 ;
;  ;
;  , где
, где  ;
;  .
.
Перестроив исходные данные (точки) на логарифмической бумаге, получим линейную зависимость, с которой легче работать и определять коэффициенты. Затем нужно пересчитать результаты по формулам, обратным исходному преобразованию.
Можно рассматривать выравнивание не как метод представления исходного динамического ряда, а как метод непосредственного приближенного определения параметров аппроксимирующей функции, что часто и делается на практике.
4. Логический отбор видов аппроксимирующей функции
На основании изучения статистических данных и логического анализа протекания изучаемого процесса из заданного массива функций отбираются наиболее приемлемые виды уравнений связи. Этот этап необходим, т.к. позволяет при отборе функций учесть основные условия протекания рассматриваемого процесса и требования, предъявляемые к математической модели. На этом этапе должны быть решены следующие вопросы:
а) является ли исследуемый показатель величиной монотонно возрастающей (убывающей), стабильной, периодической, имеющей один или несколько экстремумов;
б) ограничен ли показатель сверху или снизу каким-либо пределом;
в) имеет ли функция, определяющая процесс, точку перегиба;
г) обладает ли анализируемая функция свойством симметричности;
д) имеет ли процесс четкое ограничение развития во времени.
В качестве аппроксимирующих функций чаще всего используются различные полиномы с ограничением числа членов (степени полинома):
степенной полином 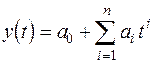 ; (11)
; (11)
экспоненциальный полином  ; (12)
; (12)
гиперболический полином 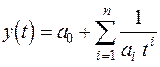 , (13)
, (13)
|
|
|
где 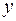 - прогнозируемый показатель;
- прогнозируемый показатель;
 - время;
- время;
 - параметры (коэффициенты), подлежащие определению.
- параметры (коэффициенты), подлежащие определению.
Опыт применения аппроксимирующих функций для целей прогнозирования показывает, что наиболее простыми (математически) и чаще всего используемыми являются следующие функции:
1) линейная  ; (14)
; (14)
2) квадратичная  (15)
(15)
( - функция роста,
- функция роста, 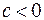 - экстремальная функция);
- экстремальная функция);
3) степенная  ; (16)
; (16)
4) экспоненциальная  ; (17)
; (17)
5) модифицированная экспонента  ; (18)
; (18)
6) гиперболическая  ; (19)
; (19)
7) логистическая кривая  , (20)
, (20)
Когда это возможно, при выборе вида аппроксимирующей функции прибегают к графическому способу подбора по виду точек временного ряда, расположенных на плоскости y0t. Если по графику подобрать функцию трудно, иногда прибегают к анализу производных от соответствующих видов функций аппроксимации (или разностей  ) соответствующего порядка.
) соответствующего порядка.
Выбирают ту функцию для прогноза, арифметическая средняя для разностного ряда которого будет равна нулю или близка к нулю по абсолютной величине.
Окончательное решение о виде аппроксимирующей функции может быть принято после определения ее параметров и верификации прогноза по ретроспективному ряду. Поэтому для прогнозирования используют несколько подходящих аппроксимирующих функций с тем, чтобы после оценки точности выбрать наиболее подходящую.
5. Оценка математической модели прогнозирования
На этом этапе исследования определяются параметры различных видов аппроксимирующих функций. Наиболее распространенными методами оценки параметров аппроксимирующих зависимостей являются метод наименьших квадратов (МНК) и его модификации, и метод экспоненциального сглаживания.
5.1 Идея метода наименьших квадратов состоит в определении параметров модели тренда, минимизирующих ее отклонение от точек исходного временного ряда: 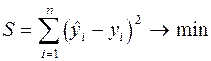 , (21)
, (21)
где  - расчетные (теоретические) значения исходного ряда;
- расчетные (теоретические) значения исходного ряда;
 - фактические значения исходного ряда;
- фактические значения исходного ряда;
 - число наблюдений.
- число наблюдений.
Классический метод наименьших квадратов предполагает равноценность исходной информации в модели. В реальной же практике будущее поведение процесса в большей степени определяется поздними наблюдениями, чем ранними. Речь идет о дисконтировании, т.е. уменьшении ценности более ранней информации.
|
|
|
Дисконтирование учитывают путем введения в модель (21) некоторых весов
. Тогда
 .
.
Коэффициенты  могут быть заданы в числовой форме или в виде функциональной зависимости таким образом, чтобы по мере продвижения в прошлое веса убывали.
могут быть заданы в числовой форме или в виде функциональной зависимости таким образом, чтобы по мере продвижения в прошлое веса убывали.
Метод наименьших квадратов широко применяется при прогнозировании, что объясняется его простотой и легкостью реализации на ЭВМ.
К недостаткам МНК можно отнести следующее:
1. модель тренда жестко фиксируется, и с помощью МНК можно получить прогноз на небольшой период упреждения. Поэтому МНК относят к методам краткосрочного прогнозирования;
2.значительную трудность представляет правильный выбор вида модели, а также обоснование и выбор весов во взвешенном методе наименьших квадратов;
3.МНК очень просто реализуется только для линейных и линеаризуемых зависимостей, когда для получения оценок коэффициентов моделей решается система линейных уравнений. Задача значительно усложняется, если для прогноза используется функциональная зависимость, не сводимая к линейной.
5.2 Метод экспоненциального сглаживания является эффективным и надежным методом среднесрочного прогнозирования.
Сущность метода заключается в сглаживании исходного динамического ряда взвешенной скользящей средней, веса которой ( ) подчиняются экспоненциальному закону (см. рис. 1).
) подчиняются экспоненциальному закону (см. рис. 1).
Пусть исходный динамический ряд описывается полиномом вида
 (22)
(22)
где  - коэффициенты;
- коэффициенты;
 - порядок полинома;
- порядок полинома;
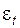 - случайная ошибка.
- случайная ошибка.
|
|







|
|
|



|

 |  | ||||||
| |||||||
|
Метод экспоненциального сглаживания позволяет построить такое описание процесса (22), при котором более поздним наблюдениям придаются большие веса по сравнению с ранними наблюдениями, причем веса наблюдений убывают по экспоненте.
Выражение  (23) называется экспоненциальной средней
(23) называется экспоненциальной средней  -го порядка для ряда
-го порядка для ряда 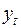 , где
, где  - параметр сглаживания.
- параметр сглаживания.
В расчетах экспоненциальную среднюю определяют, пользуясь рекуррентной формулой, полученной Брауном:
 . (24)
. (24)
Использование соотношения(24) предполагает задание начальных условий  , которые могут быть определены по формуле Брауна-Мейера
, которые могут быть определены по формуле Брауна-Мейера
 (25)
(25)
где  ;
;
 - оценки коэффициентов.
- оценки коэффициентов.
Оценки коэффициентов прогнозирующего полинома определяют через экспоненциальные средние по фундаментальной теореме Брауна-Мейера. В этом случае коэффициенты  находят решением системы (
находят решением системы ( ) уравнений с (
) уравнений с ( ) неизвестными, связывающей параметры полинома с исходной информацией.
) неизвестными, связывающей параметры полинома с исходной информацией.
|
|
|
Рассмотрим применение метода экспоненциального сглаживания для двух наиболее употребительных случаев, когда тренд описывается линейной функцией и параболой.
Линейная модель Брауна
 . (26)
. (26)
Начальные приближения для случая линейного тренда равны (по ф-ле (25)):
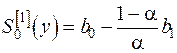 ; (27)
; (27)
 (28)
(28)
Зная начальные условия  и
и  и значение параметра
и значение параметра  , вычисляют экспоненциальные средние 1-го и 2-го порядка
, вычисляют экспоненциальные средние 1-го и 2-го порядка
 ; (29)
; (29)
 (30)
(30)
Оценки коэффициентов линейного тренда
 ; (31)
; (31)
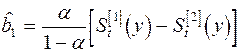 . (32)
. (32)
Прогноз на  шагов (на время
шагов (на время  ) равен
) равен 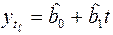 .
.
Ошибка прогноза
 . (33)
. (33)
Для метода экспоненциального сглаживания основным и наиболее трудным моментом является выбор параметра сглаживания  , начальных условий и степени прогнозирующего полинома.
, начальных условий и степени прогнозирующего полинома.
Параметр сглаживания  определяет оценки коэффициентов модели, а следовательно, результаты прогноза.
определяет оценки коэффициентов модели, а следовательно, результаты прогноза.
В зависимости от величины параметра прогнозные оценки по-разному учитывают влияние исходного ряда наблюдений: чем больше  , тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий убывает быстро. При малом
, тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий убывает быстро. При малом  прогнозные оценки учитывают все наблюдения, при этом уменьшение влияния более ранней информации происходит медленно.
прогнозные оценки учитывают все наблюдения, при этом уменьшение влияния более ранней информации происходит медленно.
Для приближенной оценки  известны два основных соотношения:
известны два основных соотношения:
1) соотношение Брауна, выведенное из условия равенства скользящей и экспоненциальной средней
 , (34)
, (34)
где  - число точек ряда, для которых динамика ряда считается однородной и устойчивой (число точек в интервале сглаживания);
- число точек ряда, для которых динамика ряда считается однородной и устойчивой (число точек в интервале сглаживания);
Иногда  , где
, где  - число наблюдений (точек) в ретроспективном динамическом ряду;
- число наблюдений (точек) в ретроспективном динамическом ряду;
2) соотношение Мейера
 , (35)
, (35)
где  - среднеквадратическая ошибка модели;
- среднеквадратическая ошибка модели;
 - среднеквадратическая ошибка исходного ряда.
- среднеквадратическая ошибка исходного ряда.
Однако достоверно определить  и
и  из исходной информации очень сложно, поэтому использование соотношения (35) затруднено.
из исходной информации очень сложно, поэтому использование соотношения (35) затруднено.
Очевидно, что выбор параметра  нужно связывать с точностью прогноза, поэтому для более обоснованного выбора
нужно связывать с точностью прогноза, поэтому для более обоснованного выбора  можно использовать процедуру обобщенного сглаживания. В этом случае получаются следующие соотношения, связывающие дисперсию прогноза
можно использовать процедуру обобщенного сглаживания. В этом случае получаются следующие соотношения, связывающие дисперсию прогноза  и параметр сглаживания
и параметр сглаживания  :
:
для линейной модели
 , (36)
, (36)
где  ;
;  - период прогноза;
- период прогноза;
 - среднеквадратическая ошибка аппроксимации исходного
- среднеквадратическая ошибка аппроксимации исходного
динамического ряда.
При  =0 выражения, стоящие в правой части формулы (36) обращаются в нуль, следовательно, для уменьшения ошибки прогноза необходимо выбирать минимальное
=0 выражения, стоящие в правой части формулы (36) обращаются в нуль, следовательно, для уменьшения ошибки прогноза необходимо выбирать минимальное  .
.
В то же время, чем меньше  , тем ниже точность определения начальных условий, а следовательно, ухудшается и качество прогноза.
, тем ниже точность определения начальных условий, а следовательно, ухудшается и качество прогноза.
Таким образом, использование формулы (36) приводит к противоречию при определении параметра сглаживания. В ряде случаев параметр  выбирают так, чтобы минимизировать ошибку прогноза, рассчитанного по ретроспективной информации.
выбирают так, чтобы минимизировать ошибку прогноза, рассчитанного по ретроспективной информации.
Качество прогноза во много зависит от выбора порядка прогнозирующего полинома. Известно, что превышение второго порядка модели не приводит к существенному увеличению точности прогноза, но значительно усложняет расчет.
Отметим в заключение, что метод экспоненциального сглаживания является одним из наиболее эффективных, надежных и широко применяемых методов прогнозирования. Он позволяет получить оценку параметров тренда, характеризующих не средний уровень процесса, а тенденцию, сложившуюся к моменту последнего наблюдения, и при этом отличается простотой вычислительных операций.
Пример 2. Пусть задан временной ряд 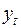 .
.
Таблица П1
| Год | ||||

| ||||
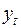
|

Рис. 2
Можно считать, что аппроксимирующая функция (тренд) описывается линейной функцией (рис.2).
1. Определим коэффициенты прямой  по методу наименьших квадратов. Для этого вычислим ряд промежуточных значений и их суммы. Результаты занесены в табл.П2. Далее найдем:
по методу наименьших квадратов. Для этого вычислим ряд промежуточных значений и их суммы. Результаты занесены в табл.П2. Далее найдем:
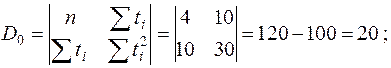
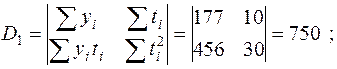

 .
.
Окончательно уравнение прямой имеет вид:  .
.
Подставив в него значения  , получим расчетные значения тренда (табл. П2).
, получим расчетные значения тренда (табл. П2).
Основная ошибка:  .
.
Таблица П2
| Год | Период | Фактическое | Расчетные значения | |||
| времени | значение 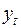
| 
| 
| 
| 
| |
| 40,2 | 0,2 | |||||
| 42,9 | -0,1 | |||||
| 45,6 | -0,4 | |||||
| 48,3 | 0,3 | |||||
| Итого | - | - |
2. Параметр сглаживания  .
.
3. Начальные условия
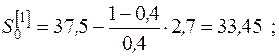
 .
.
4. Для  вычислим экспоненциальные средние
вычислим экспоненциальные средние

значения коэффициентов

прогнозируемые значения 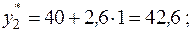
отклонения от фактического значения 
Аналогичные вычисления выполним для  =3 (1996 г.),
=3 (1996 г.),
 =4 (1997 г.),
=4 (1997 г.),  =5 (1998 г.).
=5 (1998 г.).
Результаты представим в табл.П3
Таблица П3
Типовая таблица для построения прогноза по методу
экспоненциального сглаживания
| Год | Период | Фактическое | Расчетные значения | |||||
времени 
| значение 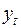
| 
| 
| 
| 
| 
| 
| |
| 2,6 | 42,6 | -0,4 | ||||||
| 38,6 | 34,6 | 42,6 | 2,7 | 45,3 | -0,7 | |||
| 41,6 | 37,4 | 45,8 | 2,8 | 48,6 | 0,6 | |||

| - | 44,2 | 40,1 | 48,3 | 2,7 | - |
Для  =3 (1996 г.)
=3 (1996 г.)



Для  =4 (1997 г.):
=4 (1997 г.):



Для построения модели прогноза на 1998 г. ( =1)
=1)


Окончательная модель прогноза имеет вид:  ,
,
где  =1, 2,... (что соответствует 1998, 1999... гг.)
=1, 2,... (что соответствует 1998, 1999... гг.)
Ошибка прогноза

6. Выбор математической модели прогнозирования
Выбор моделей прогнозирования базируется на оценке их качества. Независимо от метода оценки параметров моделей экстраполяции (прогнозирования), их качество определяется на основе исследования свойств остаточной компоненты - ( ),
),  , т.е. величины расхождений на участке аппроксимации (построения модели) между фактическими уровнями и их расчетными значениями.
, т.е. величины расхождений на участке аппроксимации (построения модели) между фактическими уровнями и их расчетными значениями.
Качество модели определяется ее адекватностью исследуемому процессу и точностью. Адекватность характеризуется наличием и учетом определенных статистических свойств, а точность степенью близости к фактическим данным. Модель прогнозирования будет считаться лучшей со статистической точки зрения, если она является адекватной и более точно описывает исходный динамический ряд.
Модель прогнозирования считается адекватной, если она учитывает существенную закономерность исследуемого процесса, в ином случае ее нельзя применять для анализа и прогнозирования.
Закономерность исследуемого процесса находит отражение в наличии определенных статистических свойств остаточной компоненты, а именно: независимости уровней, их случайности, соответствия нормальному закону распределения и равенства нулю средней ошибки.
Независимость остаточной компоненты означает отсутствие автокорреляции между остатками ( ).
).
Перечислим последствия, вызываемые автокорреляцией остатков:
1. Недооценка дисперсии остатков функции регрессии.
2. Наличие ошибки при оценке выборочной дисперсии параметров регрессии. Ошибки в вычислении дисперсий - препятствие к корректному применению метода наименьших квадратов при построении модели исходного динамического ряда.
Очевидно, важно иметь критерий, позволяющий устанавливать наличие автокорреляции. Таким критерием является критерий Дарбина-Уотсона, в соответствии с которым вычисляется статистика  :
:
 , (37)
, (37)
где  - уровни фактического динамического ряда;
- уровни фактического динамического ряда;
 - теоретические (прогнозные) уровни динамического ряда;
- теоретические (прогнозные) уровни динамического ряда;
 - объем выборки.
- объем выборки.
Возможные значения статистики лежат в интервале 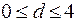 . Согласно методу Дарбина и Уотсона существует верхний
. Согласно методу Дарбина и Уотсона существует верхний  и нижний
и нижний  пределы значимости статистики
пределы значимости статистики  . Эти критические значения зависят от уровня значимости
. Эти критические значения зависят от уровня значимости  , объема выборки
, объема выборки  и числа объясняющих переменных
и числа объясняющих переменных 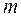 (для трендовых моделей
(для трендовых моделей 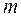 =1). В табл.1 (приложение) приведены значения
=1). В табл.1 (приложение) приведены значения  и
и  для 5 % - го уровня значимости при
для 5 % - го уровня значимости при  от 15 до 100 и числе объясняющих переменных от 1 до 5.
от 15 до 100 и числе объясняющих переменных от 1 до 5.
Вычисленное по ф-ле (37) значение  сравнивается с
сравнивается с  и
и  , найденными по табл.1 (приложение). При этом руководствуются правилами:
, найденными по табл.1 (приложение). При этом руководствуются правилами:
1. 
| принимается гипотеза: автокорреляция отсутствует; |
2. 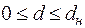
| принимается гипотеза о существовании положительной автокорреляции остатков; |

| при выбранном уровне значимости нельзя прийти к определенному выводу; |
4. 
| принимается гипотеза о существовании отрицательной автокорреляции остатков. |
Критерий Дарбина-Уотсона обладает двумя недостатками:
1. наличие области неопределенности, в которой с помощью данного критерия нельзя прийти ни к какому решению;
2. при объеме выборки меньше 15 для  не существует критических значений
не существует критических значений  и
и  . В этом случае для оценки независимости уровней ряда можно использовать коэффициент автокорреляции
. В этом случае для оценки независимости уровней ряда можно использовать коэффициент автокорреляции  :
:
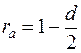 , (38)
, (38)
где  - статистика Дарбина-Уотсона.
- статистика Дарбина-Уотсона.
Расчетное значение  сравнивают с табличным
сравнивают с табличным  (табл.2 (приложение). Критическое значение коэффициента автокорреляции
(табл.2 (приложение). Критическое значение коэффициента автокорреляции  имеет одну степень свободы
имеет одну степень свободы  . Если
. Если  , то уровни динамического ряда независимы.
, то уровни динамического ряда независимы.
Для проверки случайности уровней ряда можно использовать критерий поворотных точек, который называется также критерием "пиков" и "впадин". В соответствии с этим критерием каждый уровень ряда сравнивается с двумя соединенными с ними. Если он больше или меньше их то эта точка считается поворотной. Далее подсчитывается сумма поворотных точек  . В случайном ряду чисел должно выполняться строгое неравенство:
. В случайном ряду чисел должно выполняться строгое неравенство:
 . (39)
. (39)
Соответствие ряда остатков нормальному закону распределения важно с точки зрения правомерности построения завершительных интервалов прогноза. Основными свойствами ряда остатков является их симметричность относительно тренда и преобладание малых по абсолютной величине ошибок над большими. В этой связи определяется близость к соответствующим параметрам нормального закона распределения коэффициентов асимметрии -  (мера "скошенности") и эксцесса -
(мера "скошенности") и эксцесса -  (мера "скученности") наблюдений около модели:
(мера "скученности") наблюдений около модели:
 ; (40)
; (40)
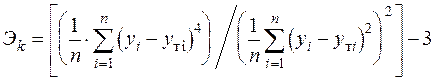 ; (41)
; (41)
Если эти коэффициенты близки к нулю или равны нулю, то ряд остатков распределен в соответствии с нормальным законом. Для оценки степени их близости к нулю вычисляют среднеквадратические отклонения:
 ; (42)
; (42)
 . (43)
. (43)
Если выполняются соотношения:
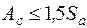 и
и  ,
,
то считается, что распределение ряда остатков не противоречит нормальному закону. В случае, когда
 или
или 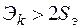 ,
,
то распределение ряда не соответствует нормальному закону распределения, и построение доверительных интервалов прогноза неправомочно. В случае попадания  и
и  в зону неопределенности (между полутора и двумя среднеквадратическими отклонениями) может быть использован
в зону неопределенности (между полутора и двумя среднеквадратическими отклонениями) может быть использован  - критерий:
- критерий:
 , (44)
, (44)
где 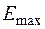 - максимальный уровень ряда остатков (
- максимальный уровень ряда остатков ( ),
),  ;
;
 - минимальный уровень ряда остатков (
- минимальный уровень ряда остатков ( ),
),  ;
;
 - среднеквадратическое отклонение остатков.
- среднеквадратическое отклонение остатков.
Если значение этого критерия попадает между табулированными границами с заданным уровнем значимости табл. 2 (приложение), то гипотеза о нормальном распределении ряда остатков принимается.
Равенство нулю средней ошибки (математическое ожидание случайной последовательности) проверяют с помощью  критерия Стьюдента:
критерия Стьюдента:
 . (45)
. (45)
Гипотеза равенства нулю средней ошибки отклоняется, если 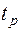 больше табличного уровня
больше табличного уровня  -критерия с
-критерия с 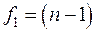 степенями свободы и выбранным уровнем значимости
степенями свободы и выбранным уровнем значимости  табл. (приложение).
табл. (приложение).
После проверки всех моделей прогнозирования из выбранного массива на адекватность, необходимо выполнить оценку их точности.
В статистическом анализе известно большое число характеристик точности. Наиболее часто в практической работе встречаются:
1. Оценка стандартной ошибки:  (46)
(46)
где  - число наблюдений;
- число наблюдений;
 - число определяемых коэффициентов модели.
- число определяемых коэффициентов модели.
2. Средняя относительная ошибка оценки:
 (47)
(47)
3. Среднее линейное отклонение  (48)
(48)
4. Ширина доверительного интервала в точке прогноза.
Для получения данной статистической оценки определим доверительный интервал в прогнозируемом периоде, т.е. возможные отклонения
|
|
|



