 |
Методы и модели корреляционно- регрессионного анализа
|
|
|
|
| 1. Общие сведения | |
| 2. Выборочные уравнения регрессии | |
| 3. Линейная регрессия | |
| 4. Основные понятия корреляционно-регрессионного анализа | |
| 5.Исходные предпосылки регрессионного анализа и свойства оценок | |
| 6.Этапы построения многофакторной корреляционно-регрессионной модели |
Общие сведения
Большинство явлений и процессов в экономике находятся в постоянной взаимной и всеохватывающей объективной связи. Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами играет большую роль в экономике. Оно дает возможность глубже понять сложный механизм причинно-следственных отношений между явлениями. Для исследования интенсивности, вида и формы зависимостей широко применяется корреляционно-регрессионный анализ, который является методическим инструментарием при решении задач прогнозирования, планирования и анализа хозяйственной деятельности предприятий.
Различают два вида зависимостей между экономическими явлениями и процессами:
- функциональная - имеется однозначное отображение множества 
на множество 
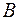. Множество называют областью определения функции, а 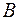- множеством значений функции. Функциональная зависимость встречается редко.
- стохастическая (вероятностную, статистическую) - зависимость между случайными величинами, при которой изменение одной из величин влечет за собой изменение закона распределения другой величины.
В большинстве случаев функция (Y) или аргумент (
) - случайные величины. и Y подвержены действию различных случайных факторов, среди которых могут быть факторы, общие для двух случайных величин. Если на случайную величину действуют факторы 
, 
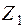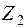,..., V 1, V 2, а на Y - 
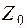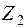, , V 1, V 3..., то наличие двух общих факторов 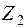и V 1 позволяет говорить о вероятностной или статистической зависимости между и Y.
|
|
|
В частном случае статистическая зависимость проявляется в том, что при изменении одной из величин изменяется математическое ожидание другой, в этом случае говорят о корреляции или корреляционной зависимости.
Статистическая зависимость проявляется только в массовом процессе, при большом числе единиц совокупности.
При стохастической закономерности для заданных значений зависимой переменной можно указать ряд значений объясняющей переменной, случайно рассеянных в интервале. Каждому фиксированному значению аргумента соответствует определенное статистическое распределение значений функции. Это обуславливается тем, что зависимая переменная, кроме выделенной переменной, подвержена влиянию ряда неконтролируемых или неучтенных факторов. Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью. В экономике приходится иметь дело со многими явлениями, имеющими вероятностный характер. Например, к числу случайных величин можно отнести: стоимость продукции, доходы предприятия, межремонтный пробег автомобилей, время ремонта оборудования и т.д.
Односторонняя вероятностная зависимость между случайными величинами есть регрессия. Она устанавливает соответствие между этими величинами.
Односторонняя стохастическая зависимость выражается с помощью функции, которая называется регрессией.
Существуют различные виды регрессий:
1. Относительно числа переменных:
простая регрессия - регрессия между двумя переменными;
множественная - регрессия между зависимой переменной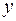 
и несколькими объясняющими переменными 
, 
,..., 
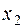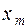. Множественная линейная регрессия имеет следующий вид:
|
|
|
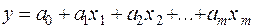, (1)
где 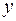- функция регрессии;
- независимые переменные;
- коэффициенты регрессии;
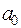- свободный член уравнения;
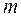- число факторов, включаемых в модель.
2. Относительно формы зависимости:
линейная регрессия, выражаемая линейной функцией;
нелинейная регрессия, выражаемая нелинейной функцией.
3. В зависимости от характера регрессии различают следующие ее виды:
положительная - имеет место, если с увеличением (уменьшением) объясняющей переменной значения зависимой переменной также соответственно увеличиваются (уменьшаются).
отрицательная - с увеличением или уменьшением объясняющей переменной зависимая переменная уменьшается или увеличивается.
4. Относительно типа соединения явлений различают:
непосредственная - зависимая и объясняющая переменные связаны непосредственно друг с другом.
косвенная - объясняющая переменная действует на зависимую через ряд других переменных.
ложная - возникает при формальном подходе к исследуемым явлениям без уяснения того, какие причины обуславливают данную связь.
Задачи регрессионного анализа:
1.Установление формы зависимости (линейная или нелинейная; положительная или отрицательная и т.д.).
2.Определение функции регрессии и установление влияния факторов на зависимую переменную. Важно не только определить форму регрессии, указать общую тенденцию изменения зависимой переменной, но и выяснить, каково было бы действие на зависимую переменную главных факторов, если бы прочие не изменялись и если были бы исключены случайные элементы. Для этого определяют функцию регрессии в виде математического уравнения того или иного типа.
3. Оценка неизвестных значений зависимой переменной, т.е. решение задач экстраполяции и интерполяции. В ходе экстраполяции распространяются тенденции, установленные в прошлом, на будущий период. Экстраполяция широко используется в прогнозировании. В ходе интерполяции определяют недостающие значения, соответствующие моментам времени между известными моментами, т.е. определяют значения зависимой переменной внутри интервала заданных значений факторов.
Регрессия тесно связана с корреляцией. Корреляция в широком смысле слова означает связь, соотношение между объективно существующими явлениями. Связи между явлениями могут быть различны по силе. При измерении тесноты связи говорят о корреляции в узком смысле слова. Если случайные переменные причинно обусловлены и можно в вероятностном смысле высказаться об их связи, то имеется корреляция.
|
|
|
Корреляция, как и регрессия, имеет различные виды:
1.Относительно характера корреляции различают:
положительную;
отрицательную.
2.Относительно числа переменных:
простую;
множественную;
частную.
3.Относительно формы связи:
линейную;
нелинейную.
4.Относительно типа соединения:
непосредственную;
косвенную;
ложную.
Задачи корреляционного анализа:
1.Измерение степени связности (тесноты, силы) двух и более явлений. Здесь речь идет в основном о подтверждении уже известных связей.
2.Отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения тесноты связи между явлениями.
3.Обнаружение неизвестных причинных связей. Корреляция непосредственно не выявляет причинных связей между явлениями, но устанавливает степень необходимости этих связей и достоверность суждений об их наличии. Причинный характер связей выясняется с помощью логически-профессиональных рассуждений, раскрывающих механизм связей.
Понятия корреляции и регрессии тесно связаны между собой. В корреляционном анализе оценивается сила связи, а в регрессионном анализе исследуется ее форма.
Любое причинное влияние может выражаться либо функциональной, либо корреляционной связью. Но не каждая функция или корреляция соответствует причинной зависимости между явлениями. Поэтому требуется обязательное исследование причинно-следственных связей.
Исследование корреляционных связей мы называем корреляционным анализом, а исследование односторонних стохастических зависимостей - регрессионным анализом.
|
|
|
