 |
Выборочные уравнения регрессии
|
|
|
|
Условное математическое ожидание случайной величины Y: 
- есть функция от 
, которая называется функцией регрессии и равна 
, т.е.
= ; (2)
аналогично:
. (3)
Графическое изображение или 
называется линией регрессии, а записанные уравнения (2) и (3) - уравнениями регрессии.
Поскольку условное математическое ожидание 
случайной величины Y есть функция от (
), то его оценка 
, т.е. условная средняя, также является функцией от . Обозначим эту функцию через
. (4)
Уравнение (5.4) определяет выборочное уравнение регрессии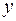 
на . Сама функция 
называется выборочной регрессией Y на , а график - выборочной регрессией. Аналогично определяется для случайных величин :
. (5)
Функция регрессии необратима, т.к. речь идет о средних величинах для некоторого конкретного значения фактора.
Функция регрессии формально устанавливает соответствие между переменными и Y, хотя такой зависимости может и не быть в экономике (ложная регрессия).
Линейная регрессия
Пусть задана система случайных величин и Y, и пусть случайные величины и Y зависимы.
Представим одну из случайных величин как линейную функцию другой случайной величины :
, (6)
где 
- параметры, которые подлежат определению.
В общем случае эти параметры могут быть определены различными способами, наиболее часто используется метод наименьших квадратов (МНК).
Функцию 
называют наилучшим приближением в смысле МНК, если математическое ожидание 
принимает наименьшее возможное значение.
В этом случае функцию называют среднеквадратической регрессией Y на . Можно доказать, что линейная среднеквадратическая регрессия имеет вид:
, (7)
где 
- математические ожидания случайных величин 
|
|
|
соответственно;
- среднеквадратические отклонения случайных величин
соответственно;
- коэффициент парной корреляции, который определяется:
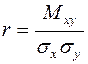, (8)
где 
- ковариация
, (9)
тогда 
- коэффициент регрессии.
Возникает проблема определения параметров 
на основе выборки.
Рассмотрим определение параметров выбранного уравнения прямой линии среднеквадратической регрессии по несгруппированным данным. Пусть изучается система количественных признаков (), т.е. ведутся наблюдения за двумерной случайной величиной (). Пусть в результате 
наблюдений получено пар чисел 
Требуется по полученным данным найти выборочное уравнение прямой линии среднеквадратической регрессии:
.
Поскольку данные несгруппированные, т.е. каждая пара чисел встречается один раз, то можно перейти от условной средней к переменной 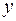. Угловой коэффициент 
обозначим через 
и назовем его выборочной оценкой коэффициента регрессии .
Итак, требуется найти:
. (10)
Очевидно, параметры 
и 
нужно подобрать так, чтобы точки 
, построенные по исходным данным, лежали как можно ближе к прямой (10) (рис. 1).
Уточним смысл этого требования. Для этого введем следующее понятие. Назовем отклонением разность вида:
,
где Yi - вычисляется по уравнению (10) и соответствует наблюдаемому
значению 
;
- наблюдаемая ордината, соответствующая .
Подберем параметры и так, чтобы сумма квадратов указанных отклонений была наименьшей:
.
В этом состоит требование метода наименьших квадратов (МНК).
Эта сумма есть функция 
отыскиваемых параметров и
или 
.
Для отыскания 
найдем частные производные и приравняем к нулю:
Далее:
Для простоты вместо 
будем писать 
(индекс 
- опускаем), тогда:
Получили систему двух линейных уравнений относительно 
и . Решая эту систему, получим:
; (11)
. (12)
Метод наименьших квадратов применяется и для нахождения параметров множественной регрессии. В этом случае число линейных уравнений возрастает, и такие системы уравнений решаются с помощью ЭВМ.
|
|
|
Основные понятия корреляционно-регрессионного анализа
1. Среднее значение переменной: 
, (13)
где - эмпирическое значение переменной ;
- число наблюдений.
2. Дисперсия: 
. (14)
3. Ковариация: 
(15)
4. Коэффициент корреляции: 
. (16)
Коэффициент корреляции характеризует тесноту или силу связи между переменным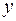и и .
Значения, принимаемые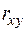 
, заключены в пределах от -1 до +1:
- при положительном значении 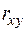имеет место положительная корреляция, т.е. с увеличением (уменьшением) значений одной переменной () значение другой (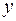) соответственно увеличивается (уменьшается);
- при отрицательном значении 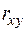имеет место отрицательная корреляция, т.е. с увеличением (уменьшением) значений значения 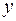соответственно уменьшаются (увеличиваются).
При изучении экономического явления, зависящего от многих факторов, строится множественная регрессионная зависимость. В этом случае для характеристики тесноты связи используется коэффициент множественной корреляции:
, (17)
где 
- остаточная дисперсия зависимой переменной;
- общая дисперсия зависимой переменной.
5. Общая дисперсия - характеризует разброс наблюдений фактических значений от среднего значения :
. (18)
6. Остаточная дисперсия характеризует ту часть рассеяния переменной 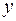, которая возникает из-за всякого рода случайностей и влияния неучтенных факторов:
, (19)
где 
- теоретические значения переменной 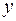, полученные по уравнению
регрессии (фор-ла 1) при подстановке в него наблюдаемых фактических значений .
7. Коэффициент детерминации служит для оценки точности регрессии, т.е. соответствия полученного уравнения регрессии имеющимся эмпирическим данным:
. (20)
Изменяется 
в пределах от 0 до 1: 
.
-если =0, это значит отношение 
=1, т.е. 
, и, следовательно, 
. В этом случае прямая регрессии будет параллельна оси , корреляционно-регрессионная связь между и 
отсутствует;
-если =1, значит =0, т.е.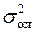 
=0. Отсюда 
- все наблюдаемые точки лежат на построенной прямой, следовательно зависимость функциональная.
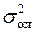Модель считается тем точнее, чем ближе к 1, т.е. чем меньше . Стандартная ошибка оценки равна 
.
|
|
|
8. Корреляционное отношение используется для оценки тесноты связи между двумя явлениями, в частности для определения тесноты связи исходного ряда с теоретическим рядом . Определяют по данным, сгруппированным по объясняющей переменной: 
. (21)
|
|
|
