Нормальные формы булевых функций

 

Нормальные формы - это особый класс аналитических выражений, используемых при решении задачи минимизации булевых функций и для перехода от табличной формы задания к аналитической. Нормальные формы строятся на основании операций конъюнкции, дизъюнкции и отрицания, причем отрицание только единственной переменной.

Определение.Элементарной конъюнкцией (дизъюнкцией) называется конъюнкция (дизъюнкция) конечного числа попарно различимых переменных или их отрицаний.

Элементарную конъюнкцию (дизъюнкцию) называют также конъюнктивным (дизъюнктивным) термом.

В частном случае терм, как конъюнктивный, так и дизъюнктивный, может состоять из единственной буквы (литерала). Под буквой будем понимать аргумент булевой функции или его отрицание.

Примерами термов являются:_.

Выражения типа: термами не являются, так как в первом случае знак отрицания стоит над двумя переменными, а во втором случае переменная x₁ находится в выражении с отрицанием и без него.

Определение. Рангом терма называется количество букв входящих в него.

 

Таблица 2.

Аргументы и функции (в символической форме)	Значения аргументов и функций	Обозначение функций	Наименование	Вырожденность	Представление функции в булевом базисе
x1
x2
						Логический ноль	+	-
					x1 & x2	Конъюнкция	-
					x1 D x2	Запрет x1 по x2	-
					x1	Повторение x1	+	-
					x2 D x1	Запрет x2 по x1	-
					x2	Повторение x2	+	-
					x1Å x2	Сумма по модулю 2, неравнозначность, исключительное ИЛИ	-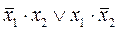
					x1Ú x2	Дизъюнкция	-
					x1¯ x2	Функция Вебба, стрелка Пирса	-
					x1~ x2 (x1º x2)	Равнозначность, эквивалентность	-
						Отрицание x2	+
					x2® x1	Импликация от x2 к x1	-
						Отрицание x1	+
					x1® x2	Импликация от x1 к x2	-
					x1ï x2	Штрих Шеффера	-
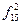
						Логическая единица	+	-

Таблица 3.

Значение аргументов	Значение функций
Сумма по модулю 2	Исключающее ИЛИ	Функция мажоритарности
x1	x2	x3	x1Å x2Å x3	XOR (x1,x2,x3)	x1#x2#x3

 

 

Определение. Дизъюнктивной (конъюнктивной) нормальной формой булевой функции называется дизъюнкция (конъюнкция) конечного числа попарно различимых конъюнктивных (дизъюнктивных) термов.

 

Определение. Конституентой единицы (нуля) называется конъюнктивный (дизъюнктивный) терм максимального ранга, т.е. для булевой функции от n переменных конституента включает в себя n букв.

 

Свойство конституенты. Конституента единицы (нуля) принимает значение единицы (нуля) на одном и только одном наборе аргументов.

Пример: При n = 4 конъюктивный терм принимает значение равное единице на наборе 1010, а дизъюнктивный терм принимает занчение равное нулю на наборе 1101.

 

Определение. Дизъюнктивная (конъюнктивная) нормальная форма называется канонической, если все ее конъюнктивные (дизъюнктивные) термы представляют собой конституенты единицы (нуля). Канонические формы называют также совершенными.

 

Замечания:

1. С помощью канонических форм наиболее просто осуществляется переход от табличной формы задания булевой функции к аналитической.

2. С помощью канонических форм любую булеву функцию можно представить в булевом базисе.

3. Любая булева функция за исключением логического нуля и логической единицы имеет единственные КДНФ и ККНФ. Логическую единицу можно представить в виде КДНФ, а логический ноль - в виде ККНФ.

4. Правило перехода от табличной формы задания булевой функции к аналитической:

а) в таблице истинности выделяются все наборы аргументов, при которых функция равна единице (нулю).

б) для каждого из этих наборов составляют конституенты единицы (нуля).

в) объединением конституенты единицы (нуля) знаками дизъюнкции (конъюнкции) получается аналитическая форма в виде КДНФ (ККНФ).

 

Пояснение. При составлении конституент единицы (нуля) используют следующее правило: Если некоторый аргумент принимает на наборе значение равное нулю, то в конституенту единицы он входит с отрицанием, а в конституенту нуля без него.

Пример: получим канонические формы для функции y = x₁ Å x_2.

x1	x2	y	Конституенты единицы	Конституенты нуля
			-
				-
				-
			-

 

КДНФ - каноническая дизъюнктивная нормальная форма:

;

ККНФ - каноническая конъюнктивная нормальная форма:

_.

КДНФ и ККНФ представляют собой две различные, но эквивалентные аналитические формы булевой функции. Это означает, что из одной формы можно получить другую, используя законы булевой алгебры.

 

Существует другой способ получения ККНФ:

а) составляется КДНФ, но не для самой булевой функции, а для ее отрицания.

б) берется отрицание над полученной КДНФ, которое снимается с применением закона двойственности.

 

4. Числовая и символическая формыпредставления булевых функций

 

Для любой булевой функции можно предложить две числовые формы, основанные на перечислении десятичных эквивалентов наборов аргументов, на которых функция принимает значение единицы (нуля).

Например:

От числовой формы легко перейти к КДНФ путем замены каждого из наборов в перечислении конституентой единицы.

.

Аналогично можно перейти к ККНФ:

 

В самом компактном виде любую булеву функцию можно представить в следующей символической форме: , где n -количество аргументов, а N -десятичный эквивалент двоичного набора значений функции на упорядоченном множестве аргументов.

Пример: f ³(Х)=x₁ Å x₂ Å x₃= - символическая форма булевой функции.

 

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: