Определение множества минимальных покрытий

 

На этом этапе из множества максимальных кубов не принадлежащих ядру покрытия, выделяются такие минимальные подмножества, с помощью каждого из которых покрываются оставшиеся вершины (не покрытые ядром). Реализацию этого этапа целесообразно производить с использованием упрощенной таблицы покрытий (табл. 6). В ней вычеркнуты все кубы, принадлежащие ядру, и вершины, покрываемые ядром.

Для решения задачи третьего этапа можно использовать один из трех методов или их комбинацию:

1) метод простого перебора;

2) метод Петрика;

3) дальнейшее упрощение таблицы покрытий.

 

Упрощенная таблица покрытий

Таблица 6

Максимальные кубы	Существенные вершины
A	000X	´	´
B	X000	´
C	0X01		´	´
D	01X1			´	´
E	X111				´	´
F	111X					´
		a	b	c	d	e

 

На данном этапе целесообразно ввести обозначение максимальных кубов и существенных вершин.

Максимальные кубы обозначены в табл. 6 прописными буквами A,..., F, а существенные вершины строчными буквами a,...,, e.

Метод целесообразно применять для упрощенной таблицы небольшого объема. Он не дает гарантии получения всех максимальных покрытий.

Для рассматриваемого примера все кубы, входящие в упрощенную таблицу покрытий, обладают одной размерностью, т.е. необходимо выбрать минимальное количество этих кубов для покрытия всех оставшихся существенных вершин.

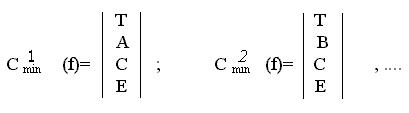Из табл. 6 видно, что минимальное число кубов равно трем. К возможным вариантам минимальных покрытий относятся:

Метод Петрика основан на составлении булева выражения, определяющего условие покрытия всех существенных вершин булевой функции из упрощенной импликантной таблицы. Булево выражение представляет собой конъюнкцию дизъюнктивных термов, каждый из которых включает в себя совокупность всех простых импликант, покрывающих одну существенную вершину функции. Полученное выражение преобразуется в дизъюнктивную форму и минимизируется с использованием законов поглощения и тавтологии. Каждый конъюктивный терм дизъюнктивной формы соответствует одному из вариантов покрытия, из которых выбирается минимальное.

Достоинство метода Петрика - получение всех минимальных покрытий.

Для рассматриваемого примера булево выражение, определяющее условие покрытия всех существенных вершин в соответствии с табл. 6 будет иметь вид:

Y= (AÚB)(AÚC)(CÚD)(DÚE)(EÚF).

Это выражение представлено в конъюктивной форме. Для его преобразования в дизъюктивную форму выполняется попарное логическое умножение дизъюетивных термов.

Замечание. В целях максимального упрощения этапа преобразования выражения Y перемножаются термы, содержащие по возможности максимальное количество букв.

После логического умножения двух первых пар дизъюктивных термов получим выражение:

Y = (AAÚACÚABÚ BC)(CDÚCEÚDDÚDE)(EÚF),

которое после применения законов тавтологии и поглощения приводится к виду:

Y = (AÚBC)(DÚCE)(EÚF).

После логического умножения последних двух скобок и последующего упрощения получим:

Y=(AÚBC)(DEÚDFÚ CEEÚCEF).

Логически умножив оставшуюся пару скобок, получим выражение Y в дизъюкнивной форме:

Y =ADEÚ ADFÚ ACEÚBCDEÚ BCDFÚ BCCE=

=ADEÚ ADFÚ ACEÚBCEÚ BCDF.

 

Каждый из пяти конъюнктивных термов соответствуют покрытию булевой функции (с учетом дополнения ядром), каждому из которых можно поставить в соответствие тупиковую ДНФ.

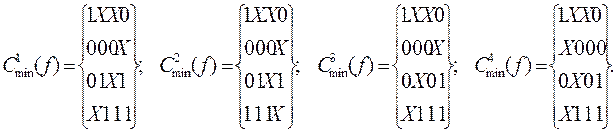Последний терм не соответствует минимальному покрытию, то есть данная функция имеет четыре минимальных покрытия.

Для всех минимальных покрытий S^a=11; S^b=15.

 

Минимальные ДНФ, соответствующие этим покрытиям:

МДНФ₁:

МДНФ₂:

МДНФ₃:

МДНФ₄:

 

Дальнейшее упрощение таблицы покрытий состоит в применении двух операций:

а) вычеркивание “лишних” строк;

б) вычеркивание “лишних” столбцов.

Операции вычеркивания строк и столбцов базируются на следующих правилах:

§ если множество меток i -й строки является подмножеством меток j -й строки и куб i имеет не большую размерность, чем куб j, то из таблицы можно вычеркнуть i -ю строку, так как существенные вершины покрываемые i -м кубом будут с гарантией покрыты j -м кубом;

§ если множество меток k –го столбца таблицы покрытий является подмножеством меток l- го столбца, то из таблицы покрытий можно вычеркнуть l –ый столбец, так как существенная вершина l будет наверняка покрыта за счет одного из кубов, покрывающих оставшуюся существенную вершину k.

Применим метод дальнейшего упрощения таблицы покрытий в отношении табл. 6. С помощью операции вычеркивания “лишних” строк из нее можно удалить две строки B и F, множество меток в которых является подмножеством меток в строках A и E соответственно. Процесс удаления “лишних” строк показан в табл. 7.

После удаления строк B и F, соответствующих максимальным кубам Х000 и 111Х получим новую упрощенную таблицу покрытий представленную в виде табл. 8. В отличие от табл. 6 (упрощенная таблица покрытий нулевого порядка) будем называть табл. 8 упрощенной таблицей покрытий первого порядка.

В табл. 8 можно выделить новое ядро покрытия T¹(f)= которое будем называть ядром покрытия первого порядка в отличие от ядра Т(f) (ядра покрытия нулевого порядка), выделяемого по исходной таблице покрытий (табл. 5).

 

Вычеркивание “лишних” строк

Таблица 7.

Максимальные кубы	Существенные вершины
A	000X	*	*
B	X000	*
C	0X01		*	*
D	01X1			*	*
E	X111				*	*
F	111X					*
		a	b	c	d	e

 

Упрощенная таблица покрытий первого порядка

Таблица 8.

Максимальные кубы	Существенные вершины
0000	0001		0111	1111
A	000X	Ä	*
C	0X01		*	*
D	01X1			*	*
E	X111				*	Ä
		a	b	c	d	e

 

После вычеркивания кубов ядра T¹(f) (строки A и E), а также существенных вершин, покрываемых кубами ядра (столбцы a, b, d, e)получим упрощенную таблицу покрытий второго порядка (табл. 9).

Упрощенная таблица покрытий второго порядка

Таблица 9.

Максимальные кубы	Существенные вершины
C	0X01	*
D	01X1	*

 

Из табл. 9 определяем два минимальных покрытия в виде двух возможных вариантов дополнения кубов ядер покрытия нулевого T (f) и первого порядка T¹(f) кубами C и D соответственно.

Таким образом с помощью метода упрощения таблицы покрытий получено только два минимальных покрытия:

в то время как с помощью метода Петрика найдены четыре минимальных покрытия, т.е. все возможные варианты.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: