Минимизация булевых функций на картах Карно

 

Одним из способов графического представления булевых функций от небольшого числа переменных являются карты Карно, которые строят как развертки кубов на плоскости. При этом вершины куба представляются клетками карты, координаты которых совпадают с координатами соответствующих вершин куба. Карта заполняется так же, как таблица истинности: значение 1 указывается в клетке, соответствующей набору, на котором функция имеет единичное значение. Значения 0 на карте обычно не отмечаются. Пример использования карт Карно для представления функций:

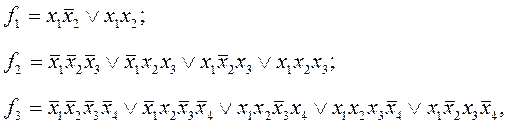
которым соответствуют комплексы:

приведен на рис.1. Клетки отмеченные на картах значениями 1, соответствуют 0-кубам (конституентам единицы) булевых функций.

x1x2

	х2х3
х1

а) f₁ б) f₂

 

 

	x3x4
x1x2

в) f₃

 

 

Рис.1. Карты Карно функций двух (а), трех (б) и четырех (в) переменных.

Карты Карно являются удобным средством для выполнения действий с булевыми функциями и, в частности, используются для минимизации булевых функций от небольшого числа переменных.

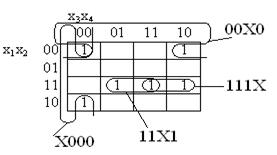
С использованием карт Карно легко выделяется минимальное покрытие функции, по которому строится ее минимальная ДНФ или КНФ. Две соседние клетки образуют 1-куб. При этом имеется в виду, что клетки, лежащие на границах карты, также являются соседними по отношению друг к другу. Примеры образования 1-кубов приведены на рис. 2 а,б.

а)

б)

Рис. 2. Образование 1- кубов.

 

Карты позволяют для функций f₁ и f₂ заданных комплексами

000 0000

001 0010

K⁰(f₁) = 011; K⁰(f₂) = 1101

100 1111

110 1110

с ценами S^а (f₁) = 15 и S^a (f₂) = 24, определить покрытия

X00 X000

С(f₁) = 0X1; C (f₂) = 00X0

1X0 11X1

111X

с ценами S^a(f₁) = 6, S^a(f₂) = 12, которым соответствуют аналитические выражения, являющиеся минимальными ДНФ функций:

Четыре вершины могут объединяться, образуя 2-куб, содержащий две независимые координаты. Примеры образования 2-кубов приведены на рис. 3.

а)	б)	в)

Рис. 3. Образование 2-кубов.

 

Карты построены для функций f₁, f₂ и f₃, заданных комплексами K⁰(f₁), K⁰(f₂), K⁰(f₃) с ценами S^a(f₁) = 40, S^a(f₂) = 24, S^a(f₃) = 32.

На картах определены покрытия состоящие из 2-кубов и имеющие цены

S^a (f₁) = 6, S^a (f₂) = 4, S^a (f₃) = 4.

Объединение восьми вершин приводит к образованию 3-куба. Примеры минимизации функций f₁, f₂, f₃, заданных комплексами

0000 0001 0000

0001 0011 0001

0011 0101 0011

0010 0111 0010

0100 1101 1000

K⁰(f₁) = 0101; K⁰(f₂) = 1111; K⁰(f₃) = 1001,

0111 1001 1011

0110 1011 1010

1100 0100 0111

1101 1100 0110

1111 0110 1111

1110 1110 1110

цена каждого из которых равна S^a = 48, приведены соответственно на картах рис. 4, а, б, в. Функциям f₁, f₂, f₃ соответствуют минимальные покрытия с ценой S^а = 2

а)	б)	в)

 

Рис. 4. Образование 3-кубов.

 

С точки зрения аналитических представлений образование (r +1)-кубов из r - кубов происходит в соответствии с правилом поглощения .

Итак, для получения минимальной ДНФ функции с использованием карты Карно определяется покрытие функции, имеющее минимальную цену. Минимальное покрытие выбирается интуитивным путем на основе анализа различных вариантов покрытий минимизируемой функции. Покрытие с минимальной ценой формируется, если каждая существенная вершина будет покрыта кубом с наибольшим числом независимых компонент и для покрытия всех существенных вершин будет использовано наименьшее число кубов.

Примеры минимизации функций приведены на рис.5. На рис. 5, а определяется минимальная форма для функции от трех переменных:

XX1 01X

имеющей цену S^а = 15. Минимальному покрытию С(f₁) =

с ценой S^а = 3 соответствует минимальная ДНФ

а)	б)
Рис. 5.Минимизация булевых функций.

На рис. 5,б приведен пример минимизации функции от четырех переменных:

0X00 X100 X111 01XX

с ценой S^а = 32. Минимальному покрытию функции С(f₂) =

с ценой S^а = 15 соответствует минимальная ДНФ:

 

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: