 |
Геометрическая интерпретация кубов малой размерности. Графическое представление булевых функций
|
|
|
|
Графическое представление булевых функций носит ограниченный характер и, как правило, является наглядным для булевых функций от 2-х и 3-х переменных.
Геометрическим местом 0-куба является точка, представляющая существенную вершину.
Два соседних 0-куба являются концами какого-либо ребра.
Геометрическим местом 1-куба является ребро, замыкаемое склеивающимися 0-кубами, образующими данный 1-куб.
Два параллельных ребра, образующих грань, являются образами склеивающихся 1-кубов. В соответствии с этим геометрической интерпретацией 2-куба является грань, образуемая парой параллельных ребер. Так как любую грань можно определить одной из пар параллельных ребер, 2-куб может быть получен как результат склеивания двух различных пар 1-кубов, то есть представляется в двух экземплярах.
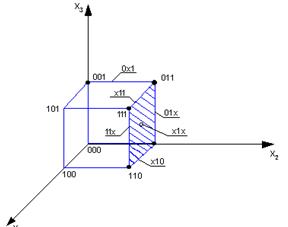Геометрическим образом 3-куба можно считать 3-х мерный куб. Так как он может быть образован 3-мя способами как пара параллельных граней, то при склеивании он получается в трех экземплярах.
По аналогии r -куб (r ³2) получается в r экземплярах как результат склеивания r различных пар (r -1) кубов.
Пример: На рисунке показано графическое представление функции 
Покрытия булевых функций
Между кубами различной размерности, входящими в кубический комплекс K(f), существует отношение включения или покрытия. Принято говорить, что куб А меньшей размерности покрывается кубом B большей размерности. Куб А включается в куб B, если при образовании куба B хотя бы в одном склеивании участвует куб А.
Отношение включения (покрытия) между кубами принято обозначать А Ì B. В теории множеств отношение включения связывает между собой некоторое множество и его подмножества.
|
|
|
Для рассмотренного примера отношения включения имеют место между следующими кубами: 001Ì0Х1; 011ÌХ11ÌХ1Х. Любой 1-куб покрывает два 0-куба, 2-куб - четыре 0-куба и четыре 1-куба, 3-куб покрывает восемь 0-кубов, двенадцать 1-кубов и шесть 2-кубов (см. геометрическую интерпретацию).
Определение. Покрытием булевой функции f называется такое подмножество кубов из кубического комплекса K(f), которое покрывает все существенные вершины функции.
В связи с тем, что любому кубу комплекса K(f) можно поставить в соответствие конъюнктивный терм, для любого покрытия можно составить некоторую ДНФ булевой функции.
Частным случаем покрытия булевой функции является кубический комплекс K0(f), покрытие C0(f)=K0(f). Этому покрытию соответствует КДНФ.
Для рассмотренного выше примера покрытием является также комплекс K1(f):
.
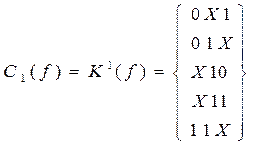Этому покрытию соответствует ДНФ вида:
Приведенная ДНФ не является минимальной.
В качестве еще одного варианта покрытия можно использовать множество максимальных кубов. Для рассмотренного выше примера
.
Действительно, кубы, входящие в Z(f), покрывают все существенные вершины: 0Х1É(001, 011), Х1ХÉ(010, 011, 110, 111).
Замечание. Множество максимальных кубов булевой функции всегда является ее покрытием.
Покрытию С2(f) соответствует ДНФ вида:
Эта ДНФ является минимальной.
Определение. Покрытие булевой функции, которое соответствует минимальной ДНФ, называется минимальным покрытием.
Замечание: Минимальное покрытие должно состоять только из максимальных кубов.
В частном случае, множество максимальных кубов может являться минимальным покрытием. Это справедливо для рассмотренного выше примера. В общем случае множество максимальных кубов является избыточным и для получения минимального покрытия достаточно выделить некоторое его подмножество.
Пример:
|
; 
;|
|
|
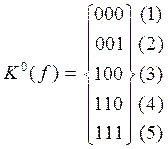Для данного примера множество максимальных кубов совпадает с комплексом K1(f): Z(f)=K1(f).
Минимальными покрытиями являются
; 
.
Определение. ДНФ, соответствующая множеству максимальных кубов, называется сокращенной (СДНФ).
Для рассматриваемого примера СДНФ:
Из анализа покрытия существенных вершин максимальными кубами из комплекса K1(f) следует:
1. Куб 00Х должен обязательно включаться в покрытие, так как он и только он покрывает существенную вершину 001, аналогично только куб 11Х покрывает существенную вершину 111.
Определение. Множество максимальных кубов, без которых не может быть образовано покрытие булевой функции, называется ядром покрытия и обозначается T(f): T(f)={00Х, 11Х}.
2. Так как ядром покрытия, кроме существенных вершин 001 и 111, покрываются также существенные вершины 000 и 110, то не покрытой ядром остается только существенная вершина 100. Для ее покрытия достаточно взять любой из оставшихся максимальных кубов: Х00 или 1Х0.
Выводы:
1. Задача получения минимальной ДНФ сводится к задаче получения минимального покрытия булевой функции.
2. В общем случае: получение минимального покрытия осуществляется в следующем порядке:
а) находится множество максимальных кубов;
б) выделяется ядро покрытия;
в) из максимальных кубов, не вошедших в ядро, выбирается такое минимальное подмножество, которое покрывает существенные вершины, не покрытые ядром.
3. Частные случаи.
1) Cmin(f) = K0(f) МДНФ=КДНФ;
2) Cmin(f) = Z(f) МДНФ=СДНФ;
3) Cmin(f) Ì Z(f);
а) Cmin(f) = T(f);
б) T(f) Ì Cmin(f);
в) T(f) = Æ.
Цена покрытия
Цена покрытия используется при решении задачи минимизации булевых функций как количественная оценка качества покрытия в смысле его минимальности. Эта оценка базируется на понятии цены кубов, составляющих покрытие.
Цена r-куба представляет собой количество несвязанных координат: Sr= n – r.
Принято использовать два вида цены покрытия:
1.
где Nr - количество r -кубов, входящих в покрытие, m - максимальная размерность кубов, входящих в покрытие. Цена Sa представляет собой сумму цен кубов, входящих в покрытие.
2.
где k - количество кубов, входящих в покрытие.
Определение. Минимальным покрытием называется покрытие, обладающее минимальной ценой Sa по сравнению с любым другим покрытием этой функции.
|
|
|
Можно показать, что покрытие, обладающее минимальной ценой Sa, обладает также и минимальной ценой Sb.
Пример:
C0(f)=K0(f); Sa =5 × 3=15; Sb=Sa +5=20;
C1(f)=K1(f); Sa =4 × 2=8; Sb=Sa +4=12;
Cmin(f): Sa =3 × 2=6; Sb =9.
Цены покрытия Sa и Sb связаны с ДНФ, соответствующей этому покрытию, следующим образом:
- цена покрытия Sa представляет собой количество букв, входящих в ДНФ;
- цена Sb представляет для ДНФ сумму количества букв и количества термов.
Цена покрытия хорошо согласуется с ценой схемы по Квайну SQ, которая строится по нормальной форме, соответствующей этому покрытию.
Для приведенной схемы цена по Квайну SQ= 9 = Sb (9 - число входов в элементы).
В принципе, между SQ и ценами Sa и Sb существует соотношение Sa £ SQ £ Sb. Это неравенство имеет место при следующих допущениях:
1. Схема строится по нормальной форме (ДНФ или КНФ).
2. Схема строится на элементах булевого базиса (И, ИЛИ).
3. На входы схемы можно подавать как прямые, так и инверсные значения входных переменных, представляющие собой значения аргументов булевой функции (схема с парафазными входами). В соответствии с этим элементы НЕ (инверторы) в схеме отсутствуют.
|
|
|
