 |
Раздел «Отношения. Функции»
|
|
|
|
Вариант № 1
1. Задано бинарное отношение r = {<1, 1>, <1, 3>, <3, 1>, <3, 4>, <4, 3>}.
Найти D (r), R (r), r 
r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не рефлексивного, не симметричного и транзитивного.
3. Дана функция f (x) = x 2 + ex, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 2
1. Задано бинарное отношение r = {<1, 3>, <3, 1>, <3, 4>, <4, 3>, <4, 4>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не симметричного, но рефлексивного и транзитивного.
3. Дана функция f (x) = x 2 + e - x , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 3
1. Задано бинарное отношение r = {<2, 2>, <2, 3>, <3, 2>, <3, 4>, <4, 1>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, но рефлексивного и симметричного.
3. Дана функция f (x) = x + ex, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 4
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <3, 3>, <4, 4>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x 2 + y 2 = 25?
|
|
|
3. Дана функция f (x) = x 3 + e x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 5
1. Задано бинарное отношение r = {<1, 2>, <2, 1>, <3, 4>, <4, 3>, <4, 4>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не симметричного, не рефлексивного и транзитивного.
3. Дана функция f (x) = x + e -- x , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 6
1. Задано бинарное отношение r = {<2, 2>, <2, 3>, <3, 2>, <3, 1>, <4, 1>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного, рефлексивного и антисимметричного.
3. Дана функция f (x) = x + e x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 7
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения рефлексивного, симметричного и транзитивного.
3. Дана функция f (x) = x 2 + 
, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 8
1. Задано бинарное отношение r = {<2, 2>, <2, 3>, <3, 2>, <3, 4>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
|
|
|
2. Привести пример отношения транзитивного, рефлексивного и антисимметричного.
3. Дана функция f (x) = x + , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 9
1. Задано бинарное отношение r = {<1, 2>, <2, 3>, <1, 3>, <1, 1>, <2, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного, рефлексивного и симметричного.
3. Дана функция f (x) = sinx + , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 10
1. Задано бинарное отношение r = {<1, 1>, <2, 3>, <1, 3>, <3, 1>, <3, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x = 2 y?
3. Дана функция f (x) = lnx + , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 11
1. Задано бинарное отношение r = {<1, 1>, <2, 4>, <1, 4>, <4, 1>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и не симметричного.
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и являющейся сюръективной, инъективной, биективной.
Вариант № 12
1. Задано бинарное отношение r = {<1, 1>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x + y = 100?
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и не являющейся сюръективной, инъективной, биективной.
|
|
|
Вариант № 13
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <3, 1>, <1, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и симметричного.
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и являющейся сюръективной, но не инъективной.
Вариант № 14
1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения рефлексивного, симметричного и транзитивного.
3. Дана функция f (x) = x 2 , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 15
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения эквивалентности.
3. Дана функция f (x) = x 2 + , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 16
1. Задано бинарное отношение r = {< b, b >, < b, c >, < c, b >, < c, a >, < d, a >}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения частичного порядка на множестве целых чисел..
3. Дана функция f (x) = x 2 + lnx, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 17
1. Задано бинарное отношение r = {< x, x >, < y, z >, < x, z >, < z, x >, < z, y >}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
|
|
|
2. Привести пример отношения транзитивного и симметричного.
3. Дана функция f (x) = x +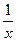 
, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 18.
1. Задано бинарное отношение r = {<1, 1>, <1, a >, < a, 1>, < a, 4>, <4, a >}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения рефлексивного и транзитивного.
3. Дана функция f (x) = x 2 + 2 x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 19
1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <2, 3>, <3, 2>, <3, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x 2 – y 2 = 0?
3. Дана функция f (x) = 2 x + , отображающая множество положительных действительных чисел во множество всех действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 20
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <3, 3>, <4, 4>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не рефлексивного, не симметричного и не транзитивного.
3. Дана функция f (x) = x 3 ex, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 21
1. Задано бинарное отношение r = {<1, 3>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения частичного порядка на множестве треугольников на плоскости.
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и не являющейся сюръективной, инъективной, биективной.
Вариант № 22
1. Задано бинарное отношение r = {<1, 2>, <2, 2>, <2, 1>, <2, 3>, <3, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством x = – y?
3. Дана функция f (x) = lnx + , отображающая множество положительных действительных чисел во множество всех действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему?
|
|
|
Вариант № 23
1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <2, 1>, <2, 3>, <3, 2>, <3, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением частичного полрядка на множестве действительных чисел отношение xry, задаваемое неравенством x 2 – y 2 £ 0?
3. Дана функция f (x) = ex + , отображающая множество положительных действительных чисел на множество положительных действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 24
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <3, 1>, <3, 2> <1, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и симметричного.
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество неотрицательных действительных чисел, R ® [0, ¥) и являющейся сюръективной, но не инъективной.
Вариант № 25
1. Задано бинарное отношение r = {<1, 2>, <2, 1>, <2, 3>, <1, 3>, <3, 1>, <3, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое неравенством x £ y?
3. Дана функция f (x) = lnx + 2 x, отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 26
1. Задано бинарное отношение r = {<2, 2>, <2, 4>, <1, 4>, <4, 1>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и не симметричного.
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и являющейся сюръективной и неинъективной.
Вариант № 27
1. Задано бинарное отношение r = {<1, 1>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xry, задаваемое равенством xy = 100?
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и не являющейся сюръективной, инъективной, биективной.
Вариант № 28
1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <3, 3>, <3, 1>, <1, 3>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и симметричного.
3. Привести пример функции f (x), отображающей множество действительных чисел R во множество действительных чисел, R ® R и являющейся сюръективной, но не инъективной.
Вариант № 29
1. Задано бинарное отношение r = {<1, 1>, <2, 2>, <4, 4>, <2, 1>, <2, 4>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения частичного порядка.
3. Дана функция f (x) = x 2 , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 30
1. Задано бинарное отношение r = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D (r), R (r), r r, r -1. Проверить, будет ли отношение r рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения эквивалентности.
3. Дана функция f (x) = x 2 + , отображающая множество действительных чисел R во множество действительных чисел, R ® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Раздел «Графы»
1. Описать граф, заданный матрицей смежности, используя как можно больше характеристик. Составить матрицу инцидентности и связности (сильной связности).
2. Пользуясь алгоритмом Форда-Беллмана, найти минимальный путь из x 1 в x 7 в ориентированном графе, заданном матрицей весов.
3. Пользуясь алгоритмом Краскала, найти минимальное остовное дерево для графа, заданного матрицей длин ребер.
Варианты заданий
1. 1. 0 1 1 0 1 1 2. ¥ 4 6 12 ¥ ¥ ¥ 3. ¥ 12 6 20 14
1 0 0 1 0 0 ¥ ¥ ¥ 13 7 ¥ ¥ 12 ¥ 2 4 6
1 0 0 0 1 0 ¥ ¥ ¥ 5 ¥ 3 ¥ 6 2 ¥ 10 12
0 1 0 0 1 0 ¥ ¥ ¥ ¥ 10 9 ¥ 20 4 10 ¥ 6
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 8 14 6 12 6 ¥
1 0 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 11
¥ ¥ ¥ ¥ ¥ ¥ ¥
2. 1. 0 0 0 0 0 1 2. ¥ 1 3 9 ¥ ¥ ¥ 3. ¥ 1 ¥ 4 5
0 0 1 1 1 0 ¥ ¥ ¥ 10 4 ¥ ¥ 1 ¥ 2 ¥ 1
0 0 0 0 0 0 ¥ ¥ ¥ 2 ¥ 1 ¥ ¥ 2 ¥ 1 1
1 0 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 ¥ 1 ¥ 3
1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 5 1 1 3 ¥
1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 8
¥ ¥ ¥ ¥ ¥ ¥ ¥
3. 1. 0 1 0 1 0 0 2. ¥ 3 5 11 ¥ ¥ ¥ 3. ¥ 6 3 10 7
1 0 0 1 0 0 ¥ ¥ ¥ 12 6 ¥ ¥ 6 ¥ 1 2 3
0 0 0 0 1 1 ¥ ¥ ¥ 3 ¥ 2 ¥ 3 1 ¥ 5 6
1 1 0 0 1 1 ¥ ¥ ¥ ¥ 9 8 ¥ 10 2 5 ¥ 3
0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 7 7 3 6 3 ¥
0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
4. 1.0 0 0 0 0 1 2. ¥ ¥ 5 4 2 2 9 3. ¥ 7 2 11 7
1 0 1 0 1 1 ¥ ¥ 1 1 ¥ 1 1 7 ¥ 3 ¥ 4
1 0 0 0 0 0 2 ¥ ¥ 1 1 ¥ 3 2 3 ¥ 1 5
0 0 1 0 0 1 ¥ 2 1 ¥ 1 ¥ ¥ 11 ¥ 1 ¥ 3
0 1 1 1 0 0 ¥ ¥ 2 2 ¥ 1 6 7 4 5 3 ¥
0 0 1 0 0 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
5. 1. 0 0 0 1 1 0 2. ¥ 4 ¥ ¥ 3 1 ¥ 3. ¥ 2 ¥ 5 5
0 0 0 1 0 1 3 ¥ 2 1 ¥ ¥ 4 2 ¥ 8 ¥ 7
1 0 0 0 0 0 1 1 ¥ ¥ ¥ ¥ 1 ¥ 8 ¥ 10 1
0 1 0 0 0 1 ¥ 3 1 ¥ 1 ¥ ¥ 5 ¥ 10 ¥ 13
1 0 0 0 0 0 ¥ ¥ 2 ¥ ¥ 1 5 5 7 1 13 ¥
0 1 0 1 0 0 ¥ 3 ¥ 2 2 ¥ ¥
¥ ¥ 2 ¥ ¥ 2 ¥
6. 1. 0 0 1 0 1 0 2. ¥ ¥ 9 ¥ ¥ 2 12 3. ¥ 1 5 4 5
0 0 1 1 1 1 1 ¥ ¥ ¥ 1 2 4 1 ¥ 2 6 1
1 1 0 0 1 0 2 1 ¥ ¥ 1 ¥ 2 5 2 ¥ 1 7
0 1 0 0 0 1 ¥ 1 1 ¥ ¥ 1 ¥ 4 6 1 ¥ 4
1 1 1 0 0 0 1 2 ¥ 2 ¥ ¥ ¥ 5 1 7 4 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ 1 ¥ 8
¥ 2 1 ¥ 1 2 ¥
7. 1. 0 0 1 1 0 0 2. ¥ 3 4 9 ¥ ¥ ¥ 3. ¥ 4 3 5 6
1 0 0 0 0 1 12 ¥ ¥ 10 4 ¥ ¥ 4 ¥ 2 ¥ 1
1 0 0 0 1 0 ¥ ¥ ¥ 2 ¥ 1 ¥ 3 2 ¥ 1 1
0 1 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 5 ¥ 1 ¥ 3
0 0 1 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 6 1 1 3 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 8
¥ ¥ ¥ ¥ ¥ ¥ ¥
8. 1. 0 1 1 0 1 1 2. ¥ 2 5 8 9 ¥ ¥ 3. ¥ 1 3 4 5
1 0 1 1 0 1 ¥ ¥ ¥ 10 4 ¥ ¥ 1 ¥ 2 9 1
1 1 0 0 1 1 5 3 ¥ 2 1 ¥ ¥ 3 2 ¥ 1 1
0 1 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 9 1 ¥ 3
1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 5 1 1 3 ¥
1 1 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 9
¥ ¥ ¥ ¥ ¥ ¥ ¥
 |
9. 1. 0 1 0 1 1 1 2. ¥ 2 5 14 ¥ ¥ ¥ 3. ¥ 5 3 10 7
1 0 0 1 0 0 11 ¥ ¥ 12 6 ¥ ¥ 5 ¥ 1 2 4
0 0 0 1 1 0 ¥ ¥ ¥ 3 ¥ 2 ¥ 3 1 ¥ 5 6
1 1 1 0 1 0 ¥ ¥ ¥ ¥ 9 8 ¥ 10 2 5 ¥ 3
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 7 7 4 6 3 ¥
1 0 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
10. 10 1 1 0 1 1 2. ¥ ¥ 5 4 2 3 9 3. ¥ 7 2 11 7
1 0 0 1 1 1 ¥ ¥ 1 1 ¥ 1 6 7 ¥ 3 ¥ 4
1 0 0 0 1 0 4 ¥ ¥ 1 1 ¥ 3 2 3 ¥ 1 5
0 1 0 0 0 1 ¥ 2 1 ¥ 1 ¥ ¥ 11 ¥ 1 ¥ 3
1 1 1 0 0 1 ¥ ¥ 2 2 ¥ 1 6 7 4 5 3 ¥
1 1 0 1 1 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
11. 1. 0 0 1 0 1 0 2. ¥ 4 9 ¥ 3 1 ¥ 3. ¥ 1 ¥ 4 5
0 0 0 1 0 1 3 ¥ 2 1 ¥ ¥ 4 1 ¥ 8 ¥ 7
1 0 0 0 1 0 1 1 ¥ ¥ 10 ¥ 1 ¥ 8 ¥ 10 1
0 1 0 0 0 1 ¥ 3 1 ¥ 1 ¥ ¥ 4 ¥ 10 ¥ 13
1 0 1 0 0 0 ¥ ¥ 2 ¥ ¥ 1 5 5 7 1 13 ¥
0 1 0 1 0 0 ¥ 3 ¥ 1 2 ¥ ¥
¥ ¥ 2 ¥ ¥ 2 ¥
 | |||||
 |  | ||||
12. 1 0 0 1 0 1 0 2. ¥ ¥ 9 ¥ 10 2 12 3. ¥ 1 5 4 6
0 0 0 1 0 1 1 ¥ ¥ ¥ 1 2 4 1 ¥ 2 6 3
1 1 0 0 1 1 2 1 ¥ ¥ 1 ¥ 2 5 2 ¥ 1 7
0 0 0 0 0 0 ¥ 1 1 ¥ ¥ 1 15 4 6 1 ¥ 4
1 1 1 0 0 0 1 2 ¥ 2 ¥ ¥ ¥ 6 3 7 4 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ 1 ¥ 8
¥ 2 1 ¥ 1 2 ¥
13. 1. 0 0 0 0 0 0 2. ¥ 5 6 15 ¥ ¥ ¥ 3. ¥ 12 6 10 4
1 0 0 1 0 1 ¥ ¥ ¥ 13 7 ¥ ¥ 12 ¥ 2 5 6
1 0 0 0 1 0 ¥ ¥ ¥ 4 ¥ 3 ¥ 6 2 ¥ 10 12
1 1 1 0 0 0 ¥ ¥ ¥ ¥ 10 9 ¥ 10 5 10 ¥ 6
1 1 0 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 8 4 6 12 6 ¥
0 1 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 11
¥ ¥ ¥ ¥ ¥ ¥ ¥
14. 1. 0 0 1 1 0 0 2. ¥ 2 3 9 ¥ ¥ ¥ 3. ¥ 3 2 4 5
1 0 0 0 0 1 12 ¥ ¥ 10 4 ¥ ¥ 3 ¥ 2 ¥ 1
1 0 0 0 1 0 ¥ ¥ ¥ 2 ¥ 1 ¥ 2 2 ¥ 1 1
0 1 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 ¥ 1 ¥ 3
0 0 1 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 5 1 1 3 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 8
¥ ¥ ¥ ¥ ¥ ¥ ¥
15. 1. 0 1 0 1 0 0 2. ¥ 2 5 10 ¥ ¥ ¥ 3. ¥ 6 3 10 4
1 0 0 1 0 0 ¥ ¥ ¥ 12 6 ¥ ¥ 6 ¥ 1 2 3
0 0 0 0 1 1 ¥ ¥ ¥ 3 ¥ 1 ¥ 3 1 ¥ 8 6
1 1 0 0 1 1 ¥ ¥ ¥ ¥ 9 8 ¥ 10 2 8 ¥ 3
0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 7 4 3 6 3 ¥
0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
 | |||||
 |  | ||||
16. 1.0 0 0 0 1 1 2. ¥ ¥ 5 4 2 2 10 3. ¥ 4 2 10 6
0 0 1 1 0 0 ¥ ¥ 2 1 ¥ 2 1 4 ¥ 3 ¥ 4
0 1 0 0 1 0 2 ¥ ¥ 1 1 ¥ 3 2 3 ¥ 1 5
0 1 0 0 0 1 ¥ 2 1 ¥ 1 ¥ ¥ 10 ¥ 1 ¥ 3
1 0 1 0 0 0 ¥ ¥ 2 2 ¥ 1 6 6 4 5 3 ¥
1 0 0 1 0 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
17. 1 0 0 1 0 1 0 2. ¥ 4 9 8 3 1 ¥ 3. ¥ 2 ¥ 3 5
0 0 0 1 0 1 3 ¥ 2 1 ¥ ¥ 4 2 ¥ 8 ¥ 7
1 0 0 0 1 0 1 1 ¥ ¥ ¥ ¥ 1 ¥ 8 ¥ 10 1
0 1 0 0 0 1 ¥ 3 1 ¥ 1 ¥ ¥ 3 ¥ 10 ¥ 12
1 0 1 0 0 0 ¥ ¥ 2 ¥ ¥ 1 5 5 7 1 12 ¥
0 1 0 1 0 0 ¥ 3 ¥ 2 2 ¥ ¥
¥ ¥ 2 ¥ ¥ 2 ¥
18. 1. 0 0 1 0 1 0 2. ¥ ¥ 9 ¥ 10 2 12 3. ¥ 1 3 4 5
0 0 0 0 0 0 1 ¥ ¥ ¥ 1 2 4 1 ¥ 2 6 8
1 0 0 0 1 0 2 1 ¥ ¥ 1 ¥ 2 3 2 ¥ 1 7
0 1 0 0 0 1 ¥ 1 1 ¥ ¥ 1 ¥ 4 6 1 ¥ 4
1 0 1 0 0 0 1 2 9 2 ¥ ¥ ¥ 5 8 7 4 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ 1 ¥ 8
¥ 2 1 ¥ 1 2 ¥
 |
19. 1. 0 1 1 0 1 1 2. ¥ 3 5 12 20 ¥ ¥ 3. ¥ 1 6 5 14
1 0 0 1 0 0 ¥ ¥ ¥ 13 8 ¥ ¥ 1 ¥ 3 4 6
1 0 0 1 1 1 ¥ ¥ ¥ 5 ¥ 3 ¥ 6 3 ¥ 10 12
0 1 1 0 1 1 ¥ ¥ ¥ ¥ 10 9 ¥ 5 4 10 ¥ 6
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 8 14 6 12 6 ¥
1 0 1 1 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 11
¥ ¥ ¥ ¥ ¥ ¥ ¥
20. 1. 0 1 0 0 1 0 2. ¥ 1 5 7 9 ¥ ¥ 3. ¥ 6 3 4 5
1 0 0 1 0 0 ¥ ¥ ¥ 10 4 ¥ ¥ 6 ¥ 2 9 1
1 0 0 0 1 1 5 3 ¥ ¥ 1 ¥ ¥ 3 2 ¥ 1 4
0 1 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 9 1 ¥ 3
0 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 4 5 1 4 3 ¥
0 1 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 9
¥ ¥ ¥ ¥ ¥ ¥ ¥
21. 1. 0 1 0 1 1 1 2. ¥ 1 5 15 ¥ ¥ ¥ 3. ¥ 5 3 6 7
1 0 0 1 0 0 ¥ ¥ 11 12 6 ¥ ¥ 5 ¥ 1 2 4
0 0 0 1 1 0 ¥ ¥ ¥ 3 ¥ 2 ¥ 3 1 ¥ 5 6
1 1 1 0 1 0 ¥ ¥ ¥ ¥ 9 8 ¥ 6 2 5 ¥ 3
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 7 7 4 6 3 ¥
1 0 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
22. 10 0 1 0 1 0 2. ¥ ¥ 3 4 1 5 9 3. ¥ 7 2 11 3
0 0 0 0 0 0 ¥ ¥ 1 2 ¥ 1 6 7 ¥ 3 ¥ 4
0 1 0 0 1 1 4 ¥ ¥ 2 1 ¥ 3 2 3 ¥ 1 5
0 1 0 0 0 1 ¥ 2 3 ¥ 1 ¥ ¥ 11 ¥ 1 ¥ 3
1 1 1 0 0 0 ¥ ¥ 2 2 ¥ 1 6 3 4 5 3 ¥
0 0 0 1 1 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
 |
23. 1. 0 0 1 0 1 0 2. ¥ 4 9 ¥ 3 1 ¥ 3. ¥ 1 9 4 5
0 0 0 1 0 1 3 ¥ 2 1 ¥ ¥ 4 1 ¥ 8 ¥ 7
1 0 0 0 1 0 1 1 ¥ ¥ 10 14 1 9 8 ¥ 10 1
0 1 0 0 0 1 ¥ 3 1 ¥ 1 ¥ ¥ 4 ¥ 10 ¥ 13
1 0 1 0 0 0 ¥ ¥ 2 ¥ ¥ 1 5 5 7 1 13 ¥
0 1 0 1 0 0 ¥ 3 ¥ 1 2 ¥ ¥
¥ ¥ 2 ¥ ¥ 2 ¥
24. 1 0 0 1 0 1 0 2. ¥ ¥ 8 ¥ 10 3 12 3. ¥ 3 2 4 6
0 0 0 1 0 0 1 ¥ ¥ ¥ 1 2 3 3 ¥ 5 6 3
0 1 0 0 1 0 2 1 ¥ ¥ 1 ¥ 2 2 5 ¥ 1 7
0 0 0 0 0 1 ¥ 1 1 ¥ ¥ 1 15 4 6 1 ¥ 4
0 1 1 0 0 0 1 2 ¥ 2 ¥ ¥ ¥ 6 3 7 4 ¥
0 1 0 0 0 0 ¥ ¥ ¥ ¥ 1 ¥ 8
¥ 2 1 ¥ 1 2 ¥
25. 1.0 0 1 0 0 1 2. ¥ ¥ 5 4 2 2 10 3. ¥ 1 2 8 5
0 0 1 1 1 1 ¥ ¥ 2 1 ¥ 2 1 1 ¥ 3 ¥ 4
1 1 0 0 0 0 2 ¥ ¥ 1 1 ¥ 3 2 3 ¥ 1 5
0 1 0 0 0 1 12 2 1 ¥ 1 ¥ ¥ 8 ¥ 1 ¥ 3
0 1 0 0 0 1 ¥ ¥ 2 2 ¥ 1 6 5 4 5 3 ¥
1 1 0 1 1 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
| | | |||
26. 1. 0 0 0 0 1 0 2. ¥ 4 9 8 3 2 ¥ 3. ¥ 2 9 3 5
0 0 0 1 0 0 3 ¥ 2 1 ¥ ¥ 5 2 ¥ 8 ¥ 7
1 0 0 0 1 0 2 1 ¥ ¥ ¥ ¥ 1 9 8 ¥ 10 1
0 1 0 0 0 1 ¥ 3 1 ¥ 1 ¥ ¥ 3 ¥ 10 ¥ 12
0 0 0 0 0 0 ¥ ¥ 2 ¥ ¥ 1 5 5 7 1 12 ¥
0 1 0 0 0 0 ¥ 3 ¥ 2 2 ¥ ¥
¥ ¥ 2 ¥ ¥ 2 ¥
|
27. 1. 0 0 1 0 1 0 2. ¥ ¥ 9 ¥ 8 1 12 3. ¥ 1 3 7 2
0 0 1 1 1 1 1 ¥ ¥ ¥ 2 2 4 1 ¥ 5 6 8
1 1 0 0 1 0 2 1 ¥ ¥ 1 ¥ 2 3 5 ¥ 1 7
0 1 0 0 0 1 ¥ 1 1 ¥ ¥ 1 ¥ 7 6 1 ¥ 4
1 1 1 0 0 0 1 2 9 2 ¥ ¥ ¥ 2 8 7 4 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ 1 ¥ 8
¥ 2 1 ¥ 1 2 ¥
28. 1. 0 1 1 0 1 1 2. ¥ 3 5 12 20 ¥ ¥ 3. ¥ 1 6 5 14
1 0 0 1 0 0 ¥ ¥ ¥ 13 8 ¥ ¥ 1 ¥ 3 4 6
1 0 0 1 1 1 ¥ ¥ ¥ 5 ¥ 3 ¥ 6 3 ¥ 10 12
0 1 1 0 1 1 ¥ ¥ ¥ ¥ 10 9 ¥ 5 4 10 ¥ 6
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 8 14 6 12 6 ¥
1 0 1 1 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 11
¥ ¥ ¥ ¥ ¥ ¥ ¥
29. 1. 0 1 0 0 1 0 2. ¥ 1 8 6 7 ¥ ¥ 3. ¥ 2 3 4 5
1 0 0 1 0 0 ¥ ¥ ¥ 10 4 ¥ ¥ 2 ¥ 6 9 1
1 0 0 0 1 1 5 3 ¥ ¥ 1 ¥ ¥ 3 6 ¥ 1 4
0 1 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 9 1 ¥ 3
0 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 4 5 1 4 3 ¥
0 1 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 9
¥ ¥ ¥ ¥ ¥ ¥ ¥
|
30. 1. 0 1 0 1 1 1 2. ¥ 2 4 13 ¥ ¥ ¥ 3. ¥ 5 3 6 4
1 0 0 1 0 0 ¥ ¥ 11 12 6 ¥ ¥ 5 ¥ 1 2 7
0 0 0 1 1 0 ¥ ¥ ¥ 3 ¥ 2 ¥ 3 1 ¥ 5 6
1 1 1 0 1 0 ¥ ¥ ¥ ¥ 9 8 ¥ 6 2 5 ¥ 3
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 7 4 7 6 3 ¥
1 0 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
Раздел «Булевы функции»
Для данной формулы булевой функции
а) найти ДНФ, КНФ, СДНФ, СКНФ методом равносильных преобразований;
б) найти СДНФ, СКНФ табличным способом (сравнить с СДНФ, СКНФ, полученными в пункте “а”);
в) указать минимальную ДНФ и соответствующую ей переключательную схему.
Варианты заданий
| Функция | Функция |
| 1. ((x V y) É Øz) V x&y&z 2. Ø(x&(y É(xVz))) 3. (x É(z&(y ~ x))) 4. Ø(x~y) É (xVz) 5. Ø(x É y) V (y É z) 6. (x&y) É (Ø(x&z) ~ x) 7. (y Éx) ~(x É z) 8. (x&Øy) É ((ØxVz) & y) 9. Ø(x~y) É (xVz) 10. Ø(x& y) É ((xVz)É y) 11.x É(y É (z É y&z)) 12. ((y& Øz) É (xVØz)) É y 13. Ø(x&(y É (x ~ z))) 14. (x É(x&(yV Ø(x ~y)Vx))) 15. Ø(x É z) V Ø(y ~ z) | 16. Ø(x~y) É (xVz) 17. x&y É (Øx&z É (xVy)) 18. (y Éx) ~(Øx É z) 19. (x&Øy É z) É (x ~ z) 20. Ø(x&y É z) É (x É y) 21. Øx É(y É (z ~x)) 22. y&Øz É (xVØz&y) 23. Ø(x&(y É(z ~ y))) 24. x É(x&(yV Ø(x ~z))) 25. Ø(x É y)V Ø(y&(x~z)) 26. Ø(x ~ y) É Ø(x ~z) 27. Ø(x É y) É (x&z) 28. x É(z É(x V y&z)) 29. x&(y É(z ~ y)) 30. Ø(x É z) V (y ~ z) |
Вопросы к экзамену по дисциплине «Дискретная математика»
1. Основные понятия теории множеств: множества, подмножества, пустое множество, универсальное множество, множество-степень.
2. Способы задания множеств.
3. Операции над множествами.
4. Геометрическое моделирование множеств. Диаграммы Эйлера - Венна.
5. Алгебра множеств. Основные тождества алгебры множеств.
6. Эквивалентность множеств. Свойство транзитивности. Мощность множества.
7. Мощность объединения конечных множеств.
8. Эквивалентность множества точек отрезков и интервалов. Теорема Бернштейна.
9. Счетные множества. Теоремы о счетных множествах.
10. Мощность множества точек отрезка [0, 1]. Теорема Кантора.
11. Множества мощности континуума. Теоремы о множествах мощности континуума.
12. Отношения. Основные понятия и определения. Бинарные отношения. Область определения, область значений и область задания бинарного отношения.
13. Операции над отношениями. Обратное отношение, Композиция отношений.
14. Свойства отношений. Рефлексивность, симметричность, транзитивность, эквивалентность.
15. Классы эквивалентности. Разбиение множеств.
16. Отношение частичного порядка.
17. Функция как бинарное отношение. Область определения и область значений функции. Равенство функций.
18. Сюръективные, инъективные, биективные функции.
19. Обратная функция. Композиция функций.
20. Способы задания функций.
21. Определение графа. Различные типы графов.
22. Матричные способы задания графов.
23. Изоморфизм графов.
24. Маршруты, циклы в неориентированном графе.
25. Пути, контуры в ориентированном графе.
26. Связность неориентированного графа. Матрица связности.
27. Связность ориентированного графа. Матрицы односторонней и сильной связности..
28. Экстремальные пути в наг
|
|
|
