 |
Определение булевой функции
|
|
|
|
Определение 4.1. Булевой функцией f (x 1, x 2,..., xn) называется произвольная функция n переменных, аргументы которой x 1, x 2,..., xn и сама функция f принимают значения 0 или 1, т. е. xi 
{0, 1}, i = 1, 2,..., n; f (x 1, x 2,..., xn) {0, 1}.
Любая булева функция может быть представлена таблицей, в левой части которой перечислены все наборы переменных (их 2 n), а в правой части – значения функции. Пример такого задания представлен в таблице 4.1.
Таблица 4.1
| x 1 x 2 x 3 | f (x 1, x 2, x 3) |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Для формирования столбца значений переменных удобен лексико-графический порядок, в соответствии с которым каждый последующий набор значений получается из предыдущего прибавлением 1 в двоичной системе счисления, например, 100 = 011+ 1.
Всего существует 22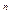 
различных булевых функций n переменных.
Функций одной переменной – 4. Из них выделим функцию “отрицание x ”(обозначается Ø x). Эта функция представлена в таблице 4.2.
Таблица 4.2
| x | Ø x |
Булевых функций двух переменных – 16 (22 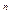при n = 2). Те из них, которые имеют специальные названия, представлены в таблице 4.3.
Таблица 4.3
| x 1 x 2 | x 1V x 2 | x 1& x 2 | x 1  x 2
| x 1~ x 2 | x 1 Å x 2 | x 1¯ x 2 | x 1ï x 2 |
| 0 0 0 1 1 0 1 1 | 0 | 1 | 1 |
В таблице 4.3 представлены следующие функции двух переменных:
x 1V x 2 – дизъюнкция;
|
|
|
x 1& x 2 – конъюнкция;
x 1É x 2 – импликация;
x 1~ x 2 – эквивалентность;
x 1Å x 2 – сложение по модулю 2;
x 1¯ x 2 – стрелка Пирса;
x 1ï x 2 – штрих Шеффера.
Остальные функции специальных названий не имеют и могут быть выражены через перечисленные выше функции.
Формулы логики булевых функций
Определение 4.2. Формула логики булевых функций определяется индуктивно следующим образом:
1. Любая переменная, а также константы 0 и 1 есть формула.
2. Если A и B – формулы, то Ø A, A V B, A & B, A É B, A ~ B есть формулы.
3. Ничто, кроме указанного в пунктах 1–2, не есть формула.
Пример 4.1.
Выражение (Ø x V y)&((y É z) ~ x) является формулой.
Выражение Ø x & y É z Ø ~ x не является формулой.
Часть формулы, которая сама является формулой, называется подформулой.
Пример 4.2.
x &(y É z) – формула; y É z – ее подформула.
Определение 4.3. Функция f есть суперпозиция функций f 1, f 2,..., fn если f получается с помощью подстановок этих формул друг в друга и переименованием переменных.
Пример 4.3.
f 1 = x 1& x 2 (конъюнкция); f 2 = Ø x (отрицание).
Возможны две суперпозиции:
1) f = f 1(f 2) = (Ø x 1)&(Ø x 2) – конъюнкция отрицаний;
2) f = f 2(f 1) = Ø(x 1& x 2) – отрицание конъюнкции.
Порядок подстановки задается формулой.
Всякая формула задает способ вычисления функции, если известны значения переменных.
Пример 4.4.
Построим таблицу значений функции f (x 1, x 2, x 3) = Ø(x 2 Ø x 3) ~ (Ø x 1V x 2).
Таблица 4.4 представляет последовательное вычисление этой функции.
Таблица 4.4
| x 1 x 2 x 3 | Ø x 3 | x 2 Ø x 3
| Ø(x 2 Ø x 3)
| Ø x 1 | Ø x 1V x 2 | f (x 1, x 2, x 3) |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Таким образом, формула каждому набору аргументов ставит в соответствие значение функции. Следовательно, формула так же, как и таблица, может служить способом задания функции. В дальнейшем формулу будем отождествлять с функцией, которую она реализует. Последовательность вычислений функции задается скобками. Принято соглашение об опускании скобок в соответствии со следующей приоритетностью операций: Ø, &, V, É и ~.
|
|
|
|
|
|
