 |
Экстремальные пути в нагруженных ориентированных графах
|
|
|
|
Ориентированный граф называется нагруженным, если дугам этого графа поставлены в соответствие веса, так что дуге (xi,xj)сопоставлено некоторое число c (xi,xj)= cij, называемое длиной ( или весом, или стоимостью дуги ). Длиной (или весом или стоимостью) пути s, состоящего из некоторой последовательности дуг (xi,xj), называется число l (s), равное сумме длин дуг, входящих в этот путь, т.е.
l (s)=  cij,
cij,
причем суммирование ведется по всем дугам(xi, xj)  s.
s.
Матрица C = (cij) называется матрицей длин дуг или матрицей весов.

Рис. 3.10
Для графа, изображенного на рис. 3.10, матрица C имеет вид:
C = 
Длина пути (x 1, x 2, x 5, x 4) равна 1 + 5 + 6 = 12.
Для ненагруженного графа введем понятие кратчайшего пути. Это путь с минимальным общим числом дуг, причем каждая дуга считается столько раз, сколько она содержится в этом пути.
Для нахождения минимального пути между двумя произвольными вершинами для случая, когда все cij ³0 можно воспользоваться простым алгоритмом Дейкстры [2]. В общем случае задача решается с помощью алгоритмов Флойда, Форда, Беллмана и др. [2,3,5].
Алгоритмы нахождения минимального пути могут быть использованы для поиска кратчайших путей в ориентированном графе без контуров. Для этого нужно каждой дуге приписать вес, равный единице.
Алгоритм Форда – Беллмана нахождения минимального пути
Предполагается, что ориентированный граф не содержит контуров отрицательной длины.
Алгоритм 3.1 (Алгоритм Форда – Беллмана).
Основными вычисляемыми величинами этого алгоритма являются величины lj (k), где i = 1, 2, …, n (n – число вершин графа); k = 1, 2, …, n – 1. Для фиксированных i и k величина lj (k) равна длине минимального пути, ведущего из заданной начальной вершины х 1в вершину хi и содержащего не более k дуг.
|
|
|
Шаг 1. Установка начальных условий.
Ввести число вершин графа n и матрицу весов C = (cij).
Шаг 2. Положить k = 0. Положить li (0) = ¥ для всех вершин, кроме х 1; положить l 1(0) = 0.
Шаг 3. В цикле по k, k = 1,..., n – 1, каждой вершине xi на k -ом шаге приписать индекс li (k) по следующему правилу:
li (k) =  { lj (k – 1)+ cji } (3.1)
{ lj (k – 1)+ cji } (3.1)
для всех вершин, кроме х 1, положить l 1(k) = 0.
В результате работы алгоритма формируется таблица индексов li (k), i = 1, 2, …, n, k = 0, 1, 2, …, n – 1. При этом li (k) определяет длину минимального пути из первой вершины в i -ую, содержащего не более k дуг.
Шаг 5. Восстановление минимального пути.
Для любойвершины xs предшествующая ей вершина xr определяется из соотношения:
lr (n – 2) + crs = ls (n – 1), xr Î G- 1(xs), (3.2)
где G- 1(xs) - прообраз вершины xs.
Для найденной вершины xr предшествующая ей вершина xq определяется из соотношения:
lq (n – 3) + cqr = lr (n – 2), xq Î G- 1(xr),
где G- 1(xr) - прообраз вершины xr, и т. д.
Последовательно применяя это соотношение, начиная от последней вершины xi, найдем минимальный путь.
Пример 3.15.
С помощью алгоритма 3.1 найдем минимальный путь из вершины х 1 в вершину х 3 в графе, изображенном на рис. 3.10.

Рис. 3.10
Рассмотрим подробно работу алгоритма Форда – Беллмана для этого примера. Значения индексов li (k) будем заносить в таблицу индексов (табл. 3.1).
Шаг 1. Введем число вершин графа n =5. Матрица весов этого графа имеет вид:
C = 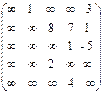 .
.
Шаг 2. Положим k = 0, l 1(0) = 0, l 2(0) = l 3(0) = l 4(0) = l 5(0) = ¥. Эти значения занесем в первый столбец табл. 3.1.
Шаг 3.
k = 1.
l 1(1) = 0.
Равенство (7.1) для k = 1 имеет вид:
li (1) =  { lj (0) + cji }.
{ lj (0) + cji }.
l 2(1) = min { l 1(0) + c 12; l 2(0) + c 22; l 3(0) + c 32; l 4(0) + c 42; l 5(0) + c 52;} = min {0 + 1; ¥ + ¥; ¥ + ¥; ¥ + ¥; ¥ + ¥} = 1.
l 3(1) = min { l 1(0) + c 13; l 2(0) + c 23; l 3(0) + c 33; l 4(0) + c 43; l 5(0) + c 53;} = min {0 + ¥; ¥ + 8; ¥ + ¥; ¥ + 2; ¥ + ¥} = ¥.
l 4(1) = min { l 1(0) + c 14; l 2(0) + c 24; l 3(0) + c 34; l 4(0) + c 44; l 5(0) + c 54;} = min {0 + ¥; ¥ + 7; ¥ + 1; ¥ + ¥; ¥ + 4} = ¥.
l 5(1) = min { l 1(0) + c 15; l 2(0) + c 25; l 3(0) + c 35; l 4(0) + c 45; l 5(0) + c 55;} = min {0 + 3; ¥ + 1; ¥ – 5; ¥ + ¥; ¥ + ¥} = 3.
|
|
|
Полученные значения li (1) занесем во второй столбец табл. 3.1. Убеждаемся, что второй столбец, начиная со второго элемента, совпадает с первой строкой матрицы весов, что легко объясняется смыслом величин li (1), которые равны длине минимального пути из первой вершины в i -ую, содержащего не более одной дуги.
k = 2.
l 1(2) = 0.
Равенство (3.1) для k = 2 имеет вид:
li (2) =  { lj (1) + cji }.
{ lj (1) + cji }.
l 2(2) = min {0 + 1; 1 + ¥; ¥ + ¥; ¥ + ¥; 3 + ¥} = 1.
l 3(2) = min {0 + ¥; 1 + 8; ¥ + ¥; ¥ + 2; 3 + ¥} = 9.
l 4(2) = min {0 + ¥; 1 + 7; ¥ + 1; ¥ + ¥; 3 + 4} = 7.
l 5(2) = min {0 + 3; 1 + 1; ¥ – 5; ¥ + ¥; 3 + ¥} = 2.
Полученные значения li (2) занесем в третий столбец табл. 3.1. Величины li (2) равны длине минимального пути из первой вершины в i -ую, содержащего не более двух дуг.
k = 3.
l 1(3) = 0.
Равенство (3.1) для k = 3 имеет вид:
li (3) =  { lj (2) + cji }.
{ lj (2) + cji }.
l 2(3) = min {0 + 1; 1 + ¥; 9 + ¥; 7 + ¥; 2 + ¥} = 1.
l 3(3) = min {0 + ¥; 1 + 8; 9 + ¥; 7 + 2; 2 + ¥} = 9.
l 4(3) = min {0 + ¥; 1 + 7; 9 + 1; 7 + ¥; 2 + 4} = 6.
l 5(3) = min {0 + 3; 1 + 1; 9 – 5; 7 + ¥; 2 + ¥} = 2.
Полученные значения li (3) занесем в четвертый столбец табл. 3.1. Величины li (3) равны длине минимального пути из первой вершины в i -ую, содержащего не более трех дуг.
k = 4.
l 1(4) = 0.
Равенство (3.1) для k = 4 имеет вид:
li (4) =  { lj (3) + cji }.
{ lj (3) + cji }.
l 2(4) = min {0 + 1; 1 + ¥; 9 + ¥; 6 + ¥; 2 + ¥} = 1.
l 3(4) = min {0 + ¥; 1 + 8; 9 + ¥; 6 + 2; 2 + ¥} = 8.
l 4(4) = min {0 + ¥; 1 + 7; 9 + 1; 6 + ¥; 2 + 4} = 6.
l 5(4) = min {0 + 3; 1 + 1; 9 – 5; 6 + ¥; 2 + ¥} = 2.
Полученные значения li (4) занесем в пятый столбец табл. 3.1. Величины li (4) равны длине минимального пути из первой вершины в i -ую, содержащего не более четырех дуг.
Таблица 3.1
| I (номер вершины) | li (0) li (1) li (2) li (3) li (4) |
| 0 0 0 0 0 ¥ 1 1 1 1 ¥ ¥ 9 9 8 ¥ ¥ 7 6 6 ¥ 3 2 2 2 |
Шаг 5. Восстановление минимального пути.
Для последней вершины x 3предшествующая ей вершина xr определяется из соотношения (3.2) полученного при s =3:
lr (3) + cr 3 = l 3(4), xr Î G- 1(x 3), (3.3)
где G- 1(x 3) - прообраз вершины x 3.
G- 1(x 3)= { x 2, x 4}.
Подставим в (3.3) последовательно r = 2 и r = 4, чтобы определить, для какого r это равенство выполняется:
l 2(3) + c 23 = 1 + 8 ¹ l 3(4) = 8,
l 4(3) + c 43 = 6 + 2 = l 3(4) = 8.
Таким образом, вершиной, предшествующей вершине x 3, является вершина x 4.
Для вершины x 4предшествующая ей вершина xr определяется из соотношения (3.2) полученного при s =4:
lr (2) + cr 4 = l 4(3), xr Î G- 1(x 4), (3.4)
где G- 1(x 4) - прообраз вершины x 4.
|
|
|
G- 1(x 4)= { x 2, x 3, x 5}.
Подставим в (3.4) последовательно r = 2, r = 3 и r = 5, чтобы определить, для какого r это равенство выполняется:
l 2(2) + c 24 = 1 + 7 ¹ l 4(3) = 6,
l 3(2) + c 34 = 1 + 1 ¹ l 4(3) = 6,
l 5(2) + c 54 = 2 + 4 = l 4(3) = 6,
Таким образом, вершиной, предшествующей вершине x 4, является вершина x 5.
Для вершины x 5предшествующая ей вершина xr определяется из соотношения (3.2) полученного при s =5:
lr (1) + cr 5 = l 5(2), xr  G- 1(x 5), (3.5)
G- 1(x 5), (3.5)
где G- 1(x 5) - прообраз вершины x 5.
G- 1(x 5)= { x 1, x 2}.
Подставим в (3.5) последовательно r = 1 и r = 2, чтобы определить, для какого r это равенство выполняется:
l 1(1) + c 15 = 0 + 3 ¹ l 5(2) = 2,
l 2(1) + c 25 = 1 + 1 = l 5(2) = 2,
Таким образом, вершиной, предшествующей вершине x 5, является вершина x 2.
Для вершины x 2предшествующая ей вершина xr определяется из соотношения (3.2) полученного при s =2:
lr (0) + cr 2 = l 2(1), xr  G- 1(x 2), (3.6)
G- 1(x 2), (3.6)
где G- 1(x 2) - прообраз вершины x 2.
G- 1(x 2)= { x 1}.
Подставим в (3.6) r = 1, чтобы определить, выполняется ли это равенство:
l 1(0) + c 12 = 0 + 1 = l 2(1) = 1.
Таким образом, вершиной, предшествующей вершине x 2, является вершина x 1.
Итак, найден минимальный путь – x 1, x 2, x 5, x 4, x 3, его длина равна 8.
|
|
|


