II. Равномерное распределение

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

I. Свойства нормального распределения

Нормальное распределение (normal distribution), которое иногда называют гауссовым (Gaussian distribution), - одно из наиболее важнейших непрерывных распределений, используемых в управлении качеством.

Широкое применение нормального распределения обусловлено следующими причинами.

1. Нормальное распределение лежит в основе классической теории статистиче­ских выводов, базирующихся на цен­тральной предельной теореме.

2. Оно достаточно точно аппроксимирует распределения многих реальных непрерывных распределений случайных величин.

3. С помощью нормального распределения можно аппроксимировать разнообраз­ные дискретные распределения.

Математическое выражение, описывающее распределение значений непрерывной случайной величины, называется плотностью непрерывного распределения вероятно­стей (continuous probability density function).

Плотность вероятностей нормального распределения имеет вид:

(1)

где m - математическое ожидание гене­ральной совокупности;

s -среднее квадратическое отклонение;

x – одно из возможных значений случайной величины, .

Плотность этого распределения для различных значений s и m изображена на рис. 1. Она имеет вид симметричного колокола. При изменении m кривая колокола без изменения формы перемещается вдоль оси x, а изменении параметра s его форма становится шире или уже, но площадь под колокообразной кривой остается неизменной и всегда равна единице.

 

Рис. 1. Плотности вероятностей нормального распределения

Нормальное распределение обладает следующими свойствами.

• Имеет колоколообразную и симметричную форму.

• Его математическое ожидание, медиана и мода совпадают друг с другом.

• Основная масса (99,7%) нормально распределенных значений лежит в диапазоне, длина которого ограничена интервалом m ± 3s.

• Значения нормально распределенной случайной величины лежат на всей числовой оси .

Выражение (1), описывающее вид огибающей распределения ординат случайной величины вдоль оси X, именуют также дифференциальным законом распределения случайной величины X. Вероятность того, что нормально распределенная случайная величина X, попадет в некоторый диапазон (a, b) находится из выражения:

 

 

 

 

где функция[1] F (x) действительного аргумента X, определенная как вероятность события F (x) = P (X < x), называется интегральнойфункцией распределения случайной величины X:

F (x) = . (2)

Важнейшие свойства функции распределе­ния:

1) F (х) — неубывающая функция своего аргумента;

2) F (- µ) = 0;

3) F (m) = 0,5;

4) F (+µ) = l.

		F (х)

x

x

 

 

Рис. 2. Плотность вероятностей и функция нормального распределения

 

Вычисление определенного интеграла (2) вызывает определенные трудности, т.к. его решение осуществляется методом численного интегрирования. С целью широкого внедрения в практику статистических исследований математических моделей, в основе которых лежит нормальное распределение случайных величин, в технической литературе по теории вероятностей и математической статистки приводятся таблицы, содержащие результаты вычислений плотности и функции распределений для нормального закона вероятностей. Поскольку количество возможных комбинаций параметров m и s бесконечно, то при непосредственном вычислении по формулам (1) и (2) понадобилось бы бесконечное число таблиц. Однако если нормировать исходные данные, то все возможные комбинации можно привести к унифицированному виду, преобразуя нормально распределенную случайную величину X в нормализованную нормально распределенную случайную величину Z.

Величина Z равна разности междувеличиной X и математическим ожиданием гене­ральной совокупности μ, деленной на среднее квадратическое отклонение σ (стандартное отклонение – в англоязычной литературе):

(3)

Математическое ожидание стандартизованного нормального распределения (standardi­zed normal distribution) равно нулю, а среднее квадратическое отклонение — единице.

Плотность стандартизованного нормального распределения имеет вид[2]:

(4)

Таким образом, любое множество нормально распределенных величин можно пре­образовать в стандартизованную форму, а затем определить искомую вероятность по таблице интегрального стандартизованного нормального распределения (см. табл.2).

Проиллюстрируем процедуру нормирования следующим примером. Предположим математическое ожидание числа ежемесячно продаваемых компьютеров равно μ =100 единиц, а среднее квадратическое отклонение — σ = 20 ед.

Как показывает рис. 3, каждому значению переменной X соответствует нормиро­ванное значение Z, полученное с помощью формулы преобразования (3). Следовательно, число проданных компьютеров, равное 120 ед., на одну стандартную единицу превышает математическое ожидание:

,

а число 40 на три стандартные единицы (стандартных отклонения) меньше математического ожидания:

 

Таким образом, среднее квадратическое отклонение становится единицей измерения качества, позволяющее оценивать вероятность реализации реальных процессов с любыми параметрами μ и σ.

 

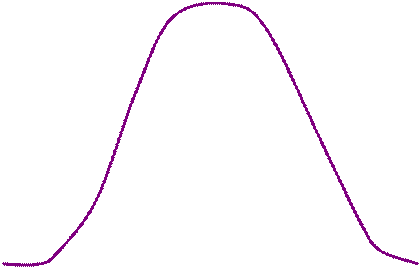
Рис. 3. Преобразование шкалы для плотности вероятностей нормального распределения к стандартизованному виду

 

Упражнение 1. Пусть по вышеприведенным условиям, необходимо определить вероятность того, что в один из случайно выбранных месяцев, количество проданных компьютеров будет:

а) не менее 90 единиц;

б) находится в диапазоне не менее 120 и не более 140 единиц;

в) менее 75 единиц.

Решение.

а). Вероятность того, что количество проданных компьютеров будет не менее 90 ед. означает, что их число может равняться 90 и любому другому числу большему 90 (см. рис.4).

Вероятность этого события равна:

Рис. 4. Преобразование шкалы для плотности вероятностей нормального распределения к стандартизованному виду

 

б).

в).

 

Определение значения переменной X _к,соответствующего заданной вероятности

Величина X равна сумме математического ожидания генеральной совокупности μ и произведения величины Z на среднее квадратическое отклонение σ:

. (5)

Чтобы вычислить конкретное значение переменной X _к, соответствующее заданной вероятности, необходимо выполнить следующее.

• Нарисовать гауссову кривую и отметить на ней математические ожидания по шкале переменных X и Z.

• Отметить и закрасить площадь фигуры, ле­жащую слева от точки X _к и ограниченную кривой нормального распределения.

• Используя данные табл. 2, определить величину Z, соответствующую суммарной пло­щади области, ограниченной нормальной кривой и лежащей слева от точки X _к.

 

Упражнение 2. Для условий упражнения 1 определите нижнюю и верхнюю границы симметричного интервала с центром в математическом ожидании нормального распределения, который содержит 95% значений случайной величины X.

Решение. Сначала определим нижнюю границу X _н, а затем — верхнюю границу Х _в. Поскольку 95% всех значений расположены между этими границами, причем величины X _н и Х _в размещены симметрично относительно математического ожида­ния, то слева и справа от этого интервала оказываются 2,5% величин.

Хотя значение X _н, неизвестно, мы можем вычислить стандартизованную величину Z,поскольку площадь фигуры, ограниченной нормальной кривой, известна и равна 0,0250.

По данным табл. 2. найдем, что Z _н = -1,96. Теперь можно вычислить значение X _н из уравнения (5).

Учитывая симметричность нормального распределения, приходим к выводу, что искомая величина Z _в равна +1,96 (поскольку эта величина лежит справа от нуля на стандартизованной шкале). Эту величину можно также получить по данным табл. 2, поскольку 97,5% площади фигуры, ограниченной нормальной кривой, лежит левее значения Z _в = +1,96.

Теперь можно вычислить значение Х _в из уравнения (5):

Х _в = 100+39,2 = 139,2.

Таким образом, 95% числа ежемесячно продаваемых компьютеров, лежат в интервале от 60,8 до 139,2 единиц.

 

Выводы.

1. Любой набор нормально распределенных случайных величин можно преобразовать в стандартизованный вид и вычислить искомые вероятности, пользуясь таблицей стан­дартизованного нормального распределения.

2. Среднее квадратическое отклонение является единицей измерения «качества» нормально распределенных случайных величин.

 

Задачи к разделу I

Задача 1. Рассмотрим стандартизованное нормальное распределение (математическое ожидание равно 0, а среднее квадратическое отклонение равно 1 (см. табл.2)).

1. Чему равна вероятность P (Z < 1,57)? 0,9418

2. Чему равна вероятность P (Z > 1,84)? 0,0329

3. Чему равна вероятность Р (1,57 < Z < 1,84 )? 0,0253

4. Чему равна вероятность P (Z < 1,57 или Z > 1,84)? 0,9747

5. Чему равна вероятность Р (-1,57 < Z < 1,84)? 0,9089

6. Чему равна вероятность P (Z < -1,57 или Z > 1,84)? 0,0911

7. Между какими значениями переменной Z (симметрично распределенной от­носительно математического ожидания) лежат 68,26% всех ее возможных значений? 1

 

Задача 2. Рассмотрим стандартизованное нормальное распределение. Вычислите следующие вероятности.

1. P (Z > +1,34).

2. P (Z <+l,17).

3. P (0< Z <+1,17).

4. Р (Z <-1,17).

5. P (-1,17< Z <+1,34).

6. P (-l,17< Z <-0,50).

 

Задача 3. Транспортная компания определила, что за год каждый из ее грузовиков проходит расстояние, равное 50,0 тыс. км, а среднее квадратическое отклонение равно 12,0 тыс. км. Предположив, что годовой пробег грузовиков распределен по нормальному закону, определите:

1. Какая доля грузовиков проходит за год от 34,0 до 50,0 тыс. км?

2. Какова вероятность того, что наугад выбранный грузовик прошел за год от 34,0 до 38,0 тыс. км?

3. Какая доля грузовиков проходит за год меньше 30,0 или больше 60,0 тыс. км?

4. Сколько из 1000 грузовиков, принадлежащих парку компании, проходят за год от 30,0 до 60,0 тыс. км?

5. Как изменятся ответы на вопросы 1-5, если среднее квадратическое отклонение равно 10,0 тыс. км?

Задача 4. Предельная нагрузка, которую выдерживают пластиковые пакеты, является нормально распределенной случайной величиной. Ее математическое ожидание равно 15 кг, а среднее квадратическое отклонение — 2,5 кг.

1. Какая доля пакетов выдерживает максимальную нагрузку не больше 17 кг?

2. Какая доля пакетов выдерживает максимальную нагрузку не меньше 14 кг?

3. Какая доля пакетов выдерживает максимальную нагрузку от 14,5 до 15,5 кг?

4. Какая доля пакетов выдерживает максимальную нагрузку от 13,2 до 14,2 кг?

5. Между какими двумя величинами (симметрично расположенными относи­тельно математического ожидания) распределены 95% всех возможных зна­чений максимальной нагрузки?

6. Как изменятся ответы на вопросы 1-5, если среднее квадратическое отклонение равно 1,0 кг?

Задача 5. Оценки, полученные студентами на экзамене по статистике, являются нормаль­но распределенными случайными величинами. Математическое ожидание этого распределения равно 73, а среднее квадратическое отклонение — 8.

1. Какова вероятностьполучить на экзамене меньше 91 баллов?

2. Какова доля студентов, получивших на экзамене от 65 до 89 баллов?

3. Какова доля студентов, получившихна экзамене от 81 до 89 баллов? Укажите сумму баллов, которую превысили только 5% студентов.

Задача 6. Статистический анализ 1 000 междугородных телефонных разговоров в офисе кор­порации «Ямис» показал, что их продолжительность
является нормально распределенной случайной величиной. Математическое ожида­ние этого распределения равно 260 с, а среднее квадратическое отклонение — 50 с

1. Какова доля разговоров, длящихся менее 130 с?

2. Какова вероятность того, что продолжительность наугад выбранного разго­вора окажется больше 130 и меньше 290 с?

3. Сколько разговоров длятся меньше 130 или больше 290 с?

4. Сколько разговоров длятся больше 110 и меньше 180 с?

II. Равномерное распределение

Случайная величина имеет равномерное распределение, если вероятность того, что она принимает любое значение в интервале, ограниченном минимальным числом а и максималь­ным числом b, постоянна. Поскольку график плотности этого распределения имеет вид прямо­угольника, равномерное распределение иногда называют прямоугольным. Плотность вероятности равномерного распределения задается формулой:

(6)

где а — минимальное значение переменной X;

b — максимальное значение переменной X.

Математическое ожидание равномерного распределения вычисляется по формуле:
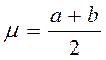. (7)

Дисперсия и среднее квадратическое отклонение равномерного распределения вычисляются соответственно по формулам:

; . (8)

D (X) = M (X - m)² = M (X ² - 2 mX + m ²) = M (X ²) - 2 mM (X) + m ² = M (X ²) - 2 m ² + m ² = M (X ²) - m ².

 

 

Задачи к разделу II.

Задача 7 (11). Предположим, что из генеральной совокупности, равномерно распределенной в интервале а = 0 и b = 10, извлекаются случайные числа.

Вычислите вероятности следующих событий:

1. Извлеченное число больше 5и меньше 7.

2. Число больше 2 и меньше 3.

3. Чему равно математическое ожидание?

4. Чему равно среднее квадратическое отклонение?

Задача 8 (12). Предположим, что время между двумя последовательными приходами клиентов в отделение банка в первой половине дня равномерно распределено в интервале от 0 до 100 с.

1. Вычислите вероятность того, что время между двумя приходами меньше 20 с.

2. Вычислите вероятность того, что время между двумя приходами больше 10 и меньше 30 с.

3. Вычислите вероятность того, что время между двумя приходами больше 35 с.

4. Чему равно математическое ожидание времени между двумя последователь­ными приходами клиентов?

5. Чему равно среднее квадратическое отклонение времени между двумя последователь­ными приходами клиентов?

 

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: