Нормированная разность между выборочной долей признака и долей признака в генеральной совокупности

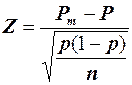(15)

 

 

Упражнение 5. Предположим, что менеджер местного отделения банка выяснил, что 40% всех вклад­чиков имеют в банке несколько счетов. Если создать выборку из 200 вкладчиков, то можно вычислить вероятность того, что выборочная доля вкладчиков, имеющих не­сколько счетов, не превосходит 0,30.

Решение. Поскольку пр = 200•0,40 = 80 > 5 и n (1- р) = 200•0,60 = 120 > 5, выборочное распреде­ление доли вкладчиков практически совпадает с нормальным.

В этом случае

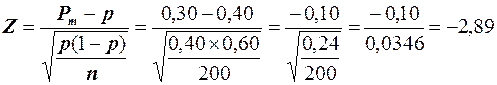
Для значения Z = -2,89 соответствует площадь 0,0019. Следовательно, веро­ятность того, что доля вкладчиков, имеющих несколько счетов, не превосходит 0,30, равна 0,0019, т.е. крайне маловероятна.

Задачи к разделу IV.

 

Задача 14 (25). В случайной выборке, состоящей из 64 человек, 48 классифицированы как «успеш­ные». Предположим, что доля успехов в генеральной совокупности равна 0,70.

1. Вычислите выборочную долю успехов . 0,75

2. Вычислите стандартную ошибку этой выборочной доли. 0,15

 

Задача 15 (26). Случайным образом выбраны 50 человек. На заданный им вопрос 15 человек ответили «Да» и 35 — «Нет». Предположим, что доля признака в генеральной совокупности равна 0,40.

1. Вычислите выборочнуюдолю .

2. Вычислите стандартную ошибку этой выборочной доли.

 

Задача 16 (28). Приблизительно 30% студентов вузов РФ являются отличниками. Предположим, что выбор­ки состоят из 100 случайно выбранных студентов.

1. Какова доля выборок, в которых количество отличников колеблется между 25 и 35%?

2. Какова доля выборок, в которых количество отличников колеблется между 20 и 40%?

3. Какова доля выборок, в которых количество отличников превышает 40%?

4. Как изменятся ответы на вопросы 1-3, если объемы выборок равны 50?

 

Задача 17 (29). По данным опроса 20% студентов вузов РФ имеют транспортные средства. Предположим, что вы­борки состоят из 100 случайно выбранных студентов.

1. Какова доля выборок, в которых количество студентов, имеющих транспортные средства, колеблется между 15 и 25%?

2. Между какими двумя процентными долями студентов, имеющих транспортные средства (симметрично расположенными относительно математиче­ского ожидания), лежат 90% выборочных процентных долей таких студентов?

3. Между какими двумя процентными долями студентов, имеющих транспортные средства (симметрично расположенными относительно математиче­ского ожидания), лежат 95% выборочных процентных долей таких cтудентов?

 

Задача 18 (30). По данным налоговых органов доля безрезультатных аудитов за 2009 г. приблизительно составляет 25%.

Предположим, что из генеральной совокупности аудитов, проведенных в 2009 г. извлекаются случай­ные выборки, состоящие из 100 аудитов.

1. Какова доля выборок, в которых количество безрезультатных аудитов колеб­лется между 24 и 26%?

2. Какова доля выборок, в которых количество безрезультатных аудитов колеб­лется между 20 и 30%?

3. Какова доля выборок, в которых количество безрезультатных аудитовпре­вышает 30%?

V. Вопросы и задачи по материалам учебного модуля

1. Перечислите свойства нормального распределения.

2. Объясните,почему менеджер по качеству должен стремиться оценить параметры генераль­ной совокупности, а не описывать свойства конкретной выборки.

3. В чем заключается разница между распределением вероятностей и выборочным распределением?

4. Объем жидкости в бутылках, содержащих безалкогольный напиток, является нор­мально распределенной случайной величиной. Математическое ожидание этого рас­пределения равно 2,0 л, а среднее квадратическое отклонение — 0,05 л. Бутылки, содержащие меньше 95% номинального объема (1,90 л), могут стать предметом судебных разби­рательств, а бутылки, содержащие более 2,10 л, опасны при открывании.

1. Какова доля бутылок, содержащих от 1,90 до 2,0 л?

2. Какова доля бутылок, содержащих от 1,90 до 2,10 л?

3. Какова доля бутылок, содержащих до 1,90 л?

4. Какова доля бутылок, содержащих меньше 1,90 или больше 2,10 л?

5. Какова доля бутылок, содержащих больше 2,10 л?

6. Какова доля бутылок, содержащих от 2,05 до 2,10 л?

7. В 99% бутылок содержится не меньше определенного объема жидкости. Чему равен этот объем?

8. Между какими двумя величинами (симметрично расположенными относительно математического ожидания) находятся объемы 99% бутылок?

9. Объясните разницу между ответами на вопросы 7 и 8.

Предположим, что из генеральной совокупности извлекается выборка, состоящая из 25 бутылок. Вычислите вероятности следующих событий.

11. Выборочное среднее больше 1,99 и меньше 2,0 л.

12. Выборочное среднее больше 1,99 и меньше 2,01 л.

13. Выборочное среднее меньше 1,98 л.

14. Выборочное среднее меньше 1,98 или меньше 2,02 л.

15. Выборочное среднее больше 2,01 л.

16. Выборочное среднее больше 2,01 и меньше 2,03 л.

17.Выше какого значения лежат 99% выборочных средних?

18. Между какими двумя величинами (симметрично расположенными относи­тельно математического ожидания) находятся объемы 99% бутылок?

 

5. По данным опроса студентов 4-го курса вуза было установлено, что их подготовка к экзаменам в зимнюю сессию в среднем составляет 12,4 часа на один экзамен. Предположим, что продолжительность подготовки к экзамену имеет нормальное распределение, среднее квадратическое отклонение которого равно 2,2 часа. Вычислите вероятность следующих событий.

1. Продолжительность подготовки к экзамену окажется меньше 10 часов?

2. Какова вероятность, что продолжительность подготовки к экзамену окажется больше 5 и меньше 15 часов?

3. Какова вероятность, что продолжительность подготовки к экзамену окажется больше 12часов?

4. Определите значение, которое не превышает продолжительность 99% времени подготовки к экзамену.

5. Между какими двумя величинами (симметрично расположенными относительно математического ожидания) находится продолжительность 93% времениподготовки к экзамену?

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: