Аппроксимация биномиального распределения

Биномиальное распределение является симметричным (как и нормальное), если р = 0,5. При р ¹ 0,5, биномиальное распределение становится несим­метричным. Однако, чем ближе параметр р к числу 0,5 и чем больше количество выбороч­ных наблюдений п, тем более симметричным становится биномиальное распределение.

С другой стороны, по мере увеличения объема выборки процесс вычисления точных вероятностей становится все более сложным, но можно использовать нормальное распределение.

Как правило, нормальное распределение можно применять, когда числа пр и п (1- р)больше пяти. Напомним, что m и s для биномиального распределения соответственно равны:

m = пр; .

Подставив эти величины в формулу преобразования, получим:

или

Следовательно, при достаточно больших значениях п случайная величина Z будет иметь приближенное значение

, (16)

где стандартную ошибку доли признака - математическое ожидание биномиального распределения; 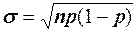- среднее квадратическое отклонение биномиального распределения;

X_а — количество успехов, скор­ректированное по дискретной величине X, т.е. X_a = X - 0,5или X_a = X + 0,5.

 

Упражнение 6. Предположим, что из крупной партии шин, содержащей 8% бракованной продук­ции, случайным образом выбраны п = 1600 шин одного типа.

Какова вероят­ность того, что в этой выборке обнаружатся не более 150 дефектных шин?

Решение. Поскольку пр = 1600 • 0,08 = 128 и п (1 - р) = 1600 • 0,92 = 1472 больше пяти, для аппроксимации биномиального распределения можно применять нор­мальное распределение.

Здесь число X_a = 150,5 является скорректированным количеством успехов.

Площадь фигуры, лежащей под нормальной кри­вой слева от точки Z = +2,07, равна 0,9808.

Вычисление приближенной вероятности по конкретному значению.

Упражнение 7. Предполо­жим, требуется вычислить вероятность того, что в выборке будет обнаружено ровно150 бракованных шин.

Решение. Поправка на непрерывность означает, что вероятность обнару­жить 150 бракованных шин равна площади фигуры, лежащей под нормальной кривой между точками 149,5 и 150,5. Следовательно, используя формулу (14), получаем:

 

Из табл. 1 находим, что площадь фигуры, лежащей под нормальной кривой слева от точки Х = 150,5 (Z = +2,07), равна 0,9808, а площадь фигуры, лежащей под нор­мальной кривой слева от точки Х =149,5 ( Z =+ l,98 ), равна 0,9761. Следовательно, приближенная вероятность того, что выборка содержит 150 бракованных шин, равна разности между этими двумя площадями, т.е. числу 0,0047.

Аппроксимация распределения Пуассона

Пуассоновское распределение можно аппроксимировать нормальным, если пара­метр λ — ожидаемое количество успехов — больше или равно пяти. Поскольку матема­тическое ожидание и дисперсия распределения Пуассона совпадают, т.е. 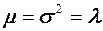, то .

Подставляя эти величины в формулу преобразования, получим

.

Таким образом, для того чтобы вычислить приближенную вероятность, соответст­вующую значениям Пуассоновской случайной величины X, можно применять форму­лу (15):

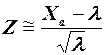, (17)

где λ — математическое ожидание распределения Пуассона, или ожидаемое количе­ство успехов;

— среднее квадратическое отклонение распределения Пуассона, X_a — ко­личество успехов, скорректированное по дискретной величине X,т.е. Х_a =Х - 0,5 или Х_a =Х + 0,5.

 

Упражнение 8. Предположим, что на автомобильном заводе среднее количество остановок работы конвейера вследствие проблем с оборудованием равно 12,0. Чему равна приближенная вероятность того, что в указанный день будет не более15 остановок работы из-за про­блем с оборудованием?

Решение.

Используя формулу (15), получаем

Здесь Х_a — скорректированное количество успехов, равное 15,5.. В табл.1 находим, что площадь фигуры, лежащей под нормальной кривой слева от точки Z = +1,01, равна 0,8438. Следовательно,приближенная вероятность того, что в указанный день будет не более15 остановок работы из-за проблем с оборудованием, равна 0,8438. Эта величина хо­рошо согласуется с истинной пуассоновской вероятностью, равной 0,8445.

Вопросы для повторения

• Почему необходимо делать поправку на непрерывность?

• В каких ситуациях биномиальное распределение можно аппроксимировать нормальным?

• В каких ситуациях распределение Пуассона можно аппроксимировать нормальным?

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: