Имитационное моделирование.

Среди признанных методов исследования сложных систем при априорной неопределенности большой интерес вызывает имитационное моделирование. Повышенное внимание к имитационному моделиро­ванию определяется не только возможностью анализа систем в ус­ловиях большой размерности и неполной информации о ее структуре, но и доступностью методологии для широкого круга специалистов-практиков, допускающей сочетание их знаний с аппаратом теории обучающихся систем, теории вероятности и математической статис­тики.

Наряду с универсальным характером и высоким уровнем де­тализации механизмов функционирования систем дополнительное до­стоинство имитационного моделирования состоит в возможности синтеза на его основе комплексных моделей, сочетающих преимущест­ва различных подходов, в том числе теории обучающихся систем.

Для преодоления априорной неопределенности структура ими­тационных моделей предполагает использование информации экспер­та, общих сведений о реальной системе, включая ее аналитическую модель, содержит блоки имитации и обработки их результатов. Выбор той или иной структуры для конкретных условий определяется уров­нем исходной информации, что может служить основой классификации методов имитационного моделирования и возникающих при этом за­дач.

Рассматриваются проблемы имитационного моделирования раз­вивающихся систем в условиях априорной неопределенности об ус­ловиях их функционирования.

Разнообразие условий исследования сложных систем обусловило появление множества методов моделирования механизмов их функ­ционирования, формирующихся вокруг аналитического и имитаци­онного направлений. Наиболее формализованными с математической точки зрения являются аналитические модели, при построении кото­рых исследователь в значительной степени абстрагируется от законо­мерностей реальной системы в рамках наиболее полно разработанных теорий. Подобная идеализация обычно сопровождается целым рядом допущений и придает аналитической модели обобщающий характер. Однако универсальность и простота модели не всегда связаны с требу­емым качеством решения задачи вследствие ограниченности мате­матических средств принятой теории либо отсутствия таковой для данных условий исследования.

Моделирование систем является трудноформализуемым процес­сом, в значительной степени определяющимся уровнем исходной ин­формации. По мере усложнения систем и увеличения априорной неоп­ределенности возникает необходимость создания специализированных методов анализа, к которым относятся имитационные модели. Станов­ление идей имитационного моделирования объясняется практически отсутствием ограничений в детализации математического описания структуры сложных систем, возможностью изучения их динамических режимов в многомерном пространстве параметров.

Понятие «имитационное моделирование» целесообразно связывать как с процессом построения математической модели системы, так и с использованием ее в машинном эксперименте для статистической оценки показателей эффективности модели. В первом случае, преодо­левая исходный барьер сложности условий исследования системы, в модели воспроизводятся реально существующие фрагменты структуры (элементы и взаимосвязи между ними) либо закономерности ее функ­ционирования. Тем самым не строится математическая модель системы (в классическом ее понимании), а описание ее поведения представля­ется комплексом локальных моделей, алгоритм взаимосвязи между которыми копирует физические процессы изучаемой системы. Такой подход часто используется при исследовании производственных про­цессов и развивающихся медико-биологических систем, когда в основу математической модели закладывается многостадийная структура тех­нологической системы либо дискретный во времени характер изме­нения некоторого множества макросостояний системы.

Второй отличительный признак имитационного моделирования за­ключается в особенности процесса предсказывания механизма функ­ционирования сложной системы, связанного с организацией вычис­лительного эксперимента на ЭВМ и обработкой полученных результа­тов. По данному признаку к классу имитационных, например, относят­ся модели типа «черный ящик», использующие принцип локальной аппроксимации.

Имитационное моделирование не исключает применения в про­цессе вычислительного эксперимента аналитических моделей при не­полной информации о начальном состоянии системы и ее входных воздействиях. Таким образом, имитационное моделирование не снижа­ет значимости аналитических моделей, а является способом расши­рения области их применения в соответствии с усложняющимися условиями исследования.

Сущность имитационного моделирования представлена на блок-схеме

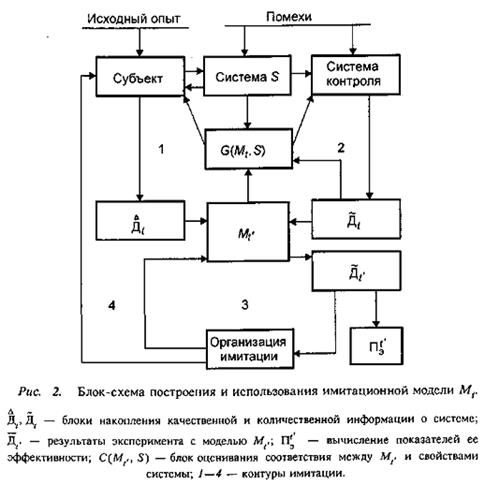
Несмотря на универсальный характер имитационного моделиро­вания, применение ее методологии наиболее целесообразно в следу­ющих условиях:

1. При наличии математической модели условия ее исследования (начальное состояние, входные переменные, параметры структуры) определяются вероятностными законами распределения.

2. При априорной неопределенности о структуре системы, когда существует возможность декомпозиции сложной системы в пространст­ве ее параметров в соответствии со значениями целевых переменных (выходных и управляющих).

3. В случае необходимости проведения многовариантных расчетов, что характерно для процессов проектирования сложных систем.

4. При исследовании систем большой сложности, экспериментиро­вание с которыми невозможно, либо требует больших материальных затрат.

5. В процессе построения обучающихся систем, тренажеров, осо­бенно при изучении временных систем большой длительности.