Структура имитационных моделей

Общепринято под структурой математической модели понимать алгоритм (S), определяющий порядок расчета выходных переменных У системы по значениям ее входов X.

Структура как способ организации целого из составных частей формируется в процессе декомпозиции системы из множества А моде­лей М_а ее подсистем, элементов и схем R сопряжения между ними

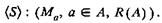
Степень конкретизации структуры модели, а следовательно, содер­жание множества А и характер R зависят от уровня исходной инфор­мации об исследуемой системе. В имитационных моделях для преодо­ления априорной неопределенности структура претерпевает сле­дующие изменения:

-вводится пара (А_п, R_n), отражающая структуру реальной систе­мы, либо последовательность действий субъекта, принимающего ре­шения. При этом не исключается использование (A, R) и их ком­бинации с (А_п, R_n);

-на основе (А_п, R_n) организуется алгоритм имитации И (А_п, R_n) с целью получения данных V для восполнения недостающих сведений о системе;

-дополнительно строится алгоритм ψ_n(V) обработки результа­тов имитации V, вид которого зависит от вида показателей эффек­тивности системы.

Если показатели являются функцией параметров системы, то при ее восстановлении также возможно использование принципов имитации. Тогда по аналогии с (2.1) структура имитационной модели представима в виде

В частности, при моделировании систем массового обслуживания по схеме множество А_п соответствует каналам обслуживания, характер R_n определяется дисциплиной обслуживания. Алгоритм И с помощью датчиков случайных чисел, воспроизводящих законы распределения промежутков времени между последовательно поступа­ющими заявками и длительности времени обслуживания, имитирует процесс функционирования системы. В операторе ψ_n(V) осуществля­ется статистическая обработка результатов многовариантных расчетов, направленных на оценивание вероятности отказов, длины очереди обслуживания, количества занятых каналов и других показателей эффективности.

В другом примере авторы при решении проблемы имита­ционного управления неопределенными объектами используют струк­туру

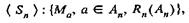
где А_п - множество макросостояний объекта, соответствующих ком­пактным траекториям управления М_а, a R_n(A_n) - алгоритм выбора модели управления М_п, реализуемый как процедура распознавания образов в пространстве параметров объекта. Тем самым осуществляет­ся обход проблемы математического моделирования путем имитации поведения субъекта-оператора при принятии решений, основанный на идее компактного соответствия между А_п и М_п. Участие субъекта в процессе синтеза структуры имитационной модели вносит неформа­лизованный элемент и затрудняет решение проблемы проверки адек­ватности модели реальной системе.

Заключение

В своей курсовой работе я попыталась рассмотреть основные свойства и закономерности построения экологических моделей, а также самые простые примеры таких моделей. Конечно же, этим далеко не исчерпывается великое многообразие ситуаций, поддающихся моделированию. Описание даже не самых сложных моделей, весьма условно приближенных к реальности, требует специальных знаний и большого количества времени. Тем более, что моделирование – постоянно развивающаяся и совершенствующаяся наука.

Эта область знаний очень прогрессивна, актуальна и, можно сказать без преувеличения, что за нею – будущее экологии. Ответственная и действенная политика по отношению к окружающей среде будет возможна лишь в том случае, если мы накопим надёжные данные о современном состоянии среды, обоснованные знания о взаимодействии важных экологических факторов, если разработаем новые методы уменьшения и предотвращения вреда, наносимого Природе Человеком. И далеко не последняя роль отводится в этом процессе математическому моделированию в экологии.

Список литературы

1. «Охрана природы» В.М.Константинов. М.: «Academa», 2000г. 240стр.

2. «Математическое моделирование в экологии» А.С.Гринин, Н.А.Орехов, В.Н.Новиков. М.: «Юнити», 2003г. 269стр.

3. «Математические модели в экологии» М.П.Федоров, М.Ф.Романов. С-Пб.: «Иван Федоров», 2003г. 240стр.

4. «Теория систем» Д.М.Жилин. М.: «УРСС», 2003г. 183стр.

5. «Имитационные модели экологических систем» А.В.Лапко, Н.В.Цугленок, Г.И.Цугленок, Новосибирск «Наука», 1999г. 185стр.

6. Ресурсы Internet: http://optics.phys.spbu.ru

http://fadr.msu.ru/rin/ecol/model.htm

http://www.gpntb.ru/win/elbib/oxrana.htm