Числовые последовательности. Придел числ.послед.

Бином Ньютона. Теорема паскаля.

Бином Ньютона: (a+b)ⁿ=aⁿ+n/1*a^n-1*b+ n(n-1)/1*2 * a^n-2b²+…+n(n-1)…(n-r+1)/1*2*3*…*r * a^n-rb^r+…+bⁿ

Теорема Паскаля. Если шестиугольник вписан в окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу, даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат на одной прямой.

Множества. Спосмобы задания. Точные границы.

Множество - это совокупность, класс отличающихся друг от друга объектов, объединенных каким-либо общим свойством. Объекты, входящие в эту совокупность, называются элементами множества. Множества обозначаются заглавными буквами латинского алфавита, а элементы множества- строчными.

Способы задания. 1.перечисление всех его элементов;2. описание характеристического (общего) свойства его элементов.

Числ. мн – во не может иметь более одной точной верхней/нижней грани. Если числ. мн – во ограничено сверху/снизу,то оно имеет одну и только одну точную верхнюю/нижнюю грань. Точная верхняя граница – наименьшая граница верхняя, мн-ва А, если она сущ. М=supA=sup{a}, a∈A. Точная нижняя граница – наибольшая нижняя граница мн-ва А, если она сущ. m<infA=inf{a}, a∈A.

3. Отрезок, интервал, ∈-окрестность, проколотая окрестность. Ограниченные и неограниченные множества.

Проколотая окрестность: Множество V называется проколотой окрестностью (выколотой окрестностью) точки x∈X, если V=V/ {x}, где V — окрестность x.

Строго говоря, проколотая окрестность не является окрестностью в смысле данного выше определения.

Интервал: эпсилон окрестности точки А. (а-ε;а+ε) ε>0, ε∈R.

Отрезок:

Огран.и неогран.мн=ва: Мн-во А наз-ся ограниченным сверху/снизу(а≥m), если сущ.число М(m), такое что для любого А∈а выполняется условие a≤m. Мн-во наз-ся огр., если оно ограниченное и сверху и снизу.m< b≤ M, IbI<k. Мн-во А наз-ся неогр.сверху/снизу(х<-ε), если для любого полож.числа А найдется хотя бы один элемент х.

4) 1.Абсолютная величина. Свойства:

Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом: если x > 0, то | x | = x; если х ≤0, то | x | = − x.

Свойства:

1."аÎR:|a|=|-a|

2."a,bÎR: |b-a|=ρ(a,b)

3.|a|≤d(d>0)ó-d≤a≤d

4.|ab|=|a|·|b|

5.|a+b|≤|a|+|b|

6.|a-b|≥||a|-|b||

Определение функции. Способы задания. Сложная функция, обратная функция. Основные элементарные функции.

функция - переменная величина, меняющаяся в зависимости от изменения другой величины.

Способы: Табличный способ. Заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

Осн элементарные ф-ии. Простейшими элементарными функциями обычно называют линейную (y=kx+b), квадратичную (y=ax2+bx+c), степенную (y=xn, где n целое число, не равно 1), показательную (y=ax,где a больше 0 и не равно 1), логарифмическую (y=loga x, где a больше 0 и не равно 1), тригонометрические (y=sin x, y=cos x, y=tg x, y=ctg x), обратные тригонометрические

(y=arcsin x, y=arccos x, y=arctg x, y=arcctg x).

1)Целая рациональная функция (или многочлен): y=a0xn+a1xn-1+...+an, где n - целое неотрицательное число (степень многочлена), a0, a1,..., an - постоянные числа (коэффициенты).

2)Дробно-рациональная функция, которая является отношением двух целых рациональных функций.

3)Иррациональная функция - это та, которая строится с помощью суперпозиции рациональной функции и степенных функций с рациональными показателями.

Сложная Функция- ( суперпози́ция фу́нкций) в математике — это применение одной функции к результату другой.

Пусть F:X→Y и G:F(X)⊂Y→Z две функции. Тогда их композицией называется функция G o F:X→Z, определённая равенством: (G o F)(x)=G(F(x)), x∈X.

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Функция g:Y→X является обратной к функции f:X→Y если для них выполнены следующие два тождества:

f(g(y)) = y для всякого y∈Y

g(f(x)) = x для всякого x∈X

Числовые последовательности. Придел числ.послед.

Числовая последовательность - функция, заданная на множестве натуральных чисел со значениями во множестве действительных чисел.

Число А называется пределом числовой последовательности {a_n}^∞_n-1, если для любого положительного e ("e>0) существует номер n такой, что при всех номерах n>n выполняется неравенство Ia_n-AI<ε. Последовательность {a_n}^∞_n-1 называется сходящейся к числу А. Кратко это можно записать так: _n=A.

7) Свойства сходящихся последовательностей: 1) Числ.послед.может иметь только один предел. 2) Ограниченность. 3) Зажатая последовательность. 4) lim x(n)=a, y(n)=b, a<b⟹x(n)<y(n), n>N(0).

Сход.послед.- послед.х_n, если она имеет конечный придел и расходящийся, если она предела не имеет.

Последовательность (x_n) действительных чисел называется сходящейся, если существует действительное число a и для произвольного ε > 0 существует натуральное число m такое, что для всех n > m справедливо неравенство |x_n - a| < ε.

При этом число a называют пределом последовательности (x_n), что символически записывают

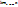_n=a или x_n → a при n → ∞.

Св-ва сходящихся посл-тей

Теорема «Об единственности пределов» Если посл-ть xn сходится, то она имеет единственный предел. Док-во (от противного) {xn} имеет два разл. Предела a и b, а¹b. Тогда согласно определению пределов любая из окрестностей т. а содержит все эл-ты посл-ти xn за исключением конечного числа и аналогичным св-вом обладает любая окрестность в точке b. Возьмем два радиуса e= (b-a)/2, т.к. эти окрестности не пересекаются, то одновременно они не могут содержать все эл-ты начиная с некоторого номера. Получим противоречие теор. док-на.

Теорема «Сходящаяся посл-ть ограничена»

Пусть посл-ть {xn}®а e >о N:"n>N½xn-a½<e эквивалентна а-e<xn<a+e "n>N => что каждый из членов посл-ти удовлетворяет неравенству½xn½£ c = max {½a-e½,½a+e½,½xn½,…,½xn-1½} Теорема «Об арифметических дейсьвиях» Пусть посл-ть {xn}®a,{yn}®b тогда арифметические операции с этими посл-тями приводят к посл-тям также имеющие пределы, причем: а) предел lim(n®¥)(xn±yn)=a±b б) предел lim(n®¥)(xn*yn)=a*b в) предел lim(n®¥)(xn/yn)=a/b, b¹0 Док-во: а)xn±yn=(а+an)±(b+bn)=(a±b)+(an±bn) Правая часть полученная в разности представляет сумму числа a+b б/м посл-тью, поэтому стоящая в левой части xn+yn имеет предел равный a±b. Аналогично др. св-ва. б) xn*yn=(а+an)*(b+bn)=ab+anb+abn+anbn an*b – это произведение const на б/м а*bn®0, anbn®0, как произведение б/м. => поэтому в правой части стоит сумма числа а*b+ б/м посл-ть. По т-ме О связи сходящихся посл-тей в б/м посл-ти в правой части xn*yn сводится к a*b. Практический вывод состоит в том, что нахожд. пределов посл-тей заданных сл. выражениями можно сводить к более простым задачам вычисления lim от составляющих этого выр-ния Посл-ть {xn} наз-ся возр., если x1<…<xn<xn+1<…;неубывающей, если x1£x2£…£xn£xn+1£…; убывающей, если x1>x2>…>xn>xn+1>…; невозр., если x1³x2³…³xn³xn+1³…Все такие посл-ти наз-ся монотонными. Возр. и убыв. наз-ся строго монотонными. Монотонные посл-ти ограничены с одной стороны, по крайней мере. Неубывающие ограничены снизу, например 1 членом, а не возрастыющие ограничены сверху. Теорема «О сходимости монотон. посл-ти» Всякая монотонная посл-ть явл-ся сходящейся, т.е. имеет пределы. Док-во Пусть посл-ть {xn} монотонно возр. и ограничена сверху. X – все мн-во чисел которое принимает эл-т этой посл-ти согласно усл. Теоремы это мн-во огранич., поэтому по соотв. Теореме оно имеет конечную точную верх. грань supX xn®supX (обозначим supX через х*). Т.к. х* точная верх. грань, то xn£x* " n. " e >0 вып-ся нер-во $ xm(пусть m- это n с крышкой):xm>x*-e при " n>m => из указанных 2-х неравенств получаем второе неравенство x*-e£xn£x*+e при n>m эквивалентно ½xn-x*½<e при n>m. Это означает, что x* явл. пределом посл-ти. 8) Б.м.послед. Св-ва б.м.послед. Бесконечно малая последовательность. Последовательность a_nпредел которой равен нулю _n=0,, называется бесконечно малой. Бесконечно малые последовательности имеют следующие свойства. 1. Сумма и разность бесконечно малых последовательностей есть также бесконечно малая последовательность.2. Бесконечно малая последовательность ограничена.3. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.4. Если {xn} – бесконечно большая последовательность, то, начиная с некоторого N, определена последовательность {1/xn}, и она есть бесконечно малая последовательность. Наоборот, если {xn} – бесконечно малая последовательность и все xn отличны от нуля, то {1/xn} есть бесконечно большая последовательность.

9) Бесконечно большие последовательности. Связь б.б.и б.м. { x_n }называется бесконечно большой, если для любого положительного числа ε, как бы велико оно не было, можно указать натуральное число N такое, что при всех n>N выполняется неравенство | x_n | > ε.

Если последовательность { x_n } является бесконечно большой, то говорят, что она имеет бесконечный предел, и пишут _n=∞. Если все члены бесконечно большой последовательности, начиная с некоторого номера положительны, то говорят также, что последовательность имеет бесконечный предел положительного знака и пишут lim x_n =+∞. Отр. аналогично. 10) Арифметические операции над сходящимися последовательностями. 1) lim пост, есть сама постоянная {x_n}=c, Ix_n-cI=o<ε=> _n=c. Предел пост.сама пост. 2) предел суммы числ. Последовательности равна сумме приделов числ.послед. 3) предел произведения числ.послед.=произведению пределов этих последовательностей. 4)предел отношений чисел послед=отношению пределов, при условии, что знаменатель не равен 0. 11) Монотонные последовательности. Критерий Вейерштрасса сходимости монотонных послед. 1) Если xn+1 > xn для всех n, то последовательность возрастающая. 2)Если xn+1 ³ xn для всех n, то последовательность неубывающая. 3)Если xn+1 < xn для всех n, то последовательность убывающая. 4)Если xn+1 £ xn для всех n, то последовательность невозрастающая Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными. Пример. {xn} = 1/n – убывающая и ограниченная, {xn} = n – возрастающая и неограниченная. Критерий. Всякая монотонная ограниченная пос-ть, имеет предел, причем _n=sup{x_n}. Если посл-ть явл.неубывающей, _n=inf{x_n} предел явл.возраст.

12. Число e. Р-рим числ. посл-ть с общим членом xn=(1+1/n)^n (в степени n)(1). Оказывается, что посл-ть (1) монотонно возр-ет, ограничена сверху и сл-но явл-ся сходящейся, предел этой пос-ти наз-ся экспонентой и обозначается символом е»2,7128…Последовательность(n→1+1/n)ⁿ,n∈N имеет конечный предел, называемый числом е: ⁿ=e=2,718281…..

13) Теорема о стягивающейся системе отрезков. Пусть даны монотонно возраст.послед-ть {x_n}и монотонно убыв.посл-ть {y_n}. {x_n}; x_n≥x₁. {y_n}; y_n≤y. x_n<y_n. y_n-x_n→0 n→∞,

=>∃ _n= _n=C. Если y_n-x_n→0 n→∞, то обе пос-ти имеют предел и этот предел то же _n= _n.

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: