 |
Необходимые и достаточные условия сущ-ия предела ф-ии.
|
|
|
|
Необходимость. A= 
Достаточность. 
19) Первый замечательный предел.Следствия.  – первый замечательный предел. Следствия. 1)
– первый замечательный предел. Следствия. 1) 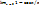 2=1/2. 2)
2=1/2. 2)  .
.
1) 3)  . 3)
. 3)  . 4)
. 4) 
20) Предел ф-ии при х→∞. при х →∞ (случаи когда х0 есть +∞ или -∞). А именно, равенство (*) во всех случаях означает следующее: для любой последовательности { хn}, сходящейся к х0, соответствующая последовательность {f(хn)} сходится к а
21) Второй замечательный предел. Следствия.  x=e. Следствия:
x=e. Следствия:
1)  x=e. 2)
x=e. 2)  1/x=e. 3)
1/x=e. 3)  =. 4)
=. 4)  x-1)/x – 1. 5)
x-1)/x – 1. 5)  x-1)/x = lna
x-1)/x = lna
22) Сравнение б.м.ф-ий. Применения для вычисления предела.
Пусть α(x) и β(x) — две функции, бесконечно малые в точке x=a. Если  , то говорят, что α(x) более высокого порядка малости, чем β(x) и обозначают α(x)=0(β(x)). Если же
, то говорят, что α(x) более высокого порядка малости, чем β(x) и обозначают α(x)=0(β(x)). Если же  , то β(x) более высокого порядка малости, чем α(x); обозначают β(x)=0(α(x)). Бесконечно малые функции α(x)и β(x) называются бесконечно малыми одного порядка малости, если
, то β(x) более высокого порядка малости, чем α(x); обозначают β(x)=0(α(x)). Бесконечно малые функции α(x)и β(x) называются бесконечно малыми одного порядка малости, если 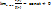 , обозначают α(x)=0(
, обозначают α(x)=0( . И, наконец, если
. И, наконец, если  не существует, то бесконечно малые функции α(x) и β(x) несравнимы.
не существует, то бесконечно малые функции α(x) и β(x) несравнимы.
Если  , то бесконечно малые функции α(x) и β(x) называются эквивалентными, обозначают α(x)~β(x).
, то бесконечно малые функции α(x) и β(x) называются эквивалентными, обозначают α(x)~β(x).
23) Непрерывность ф-ии. Функция f(x) называется непрерывной в точке x=x0, если ее предел в этой точке равен значению функции в этой точке. Условия непрерывности:1)х0∈D(f) 2)∃  3)
3)  ∀ε>0,∃δ>0:lx-x0l<δ=>lf(x)-f(x0)l<ε. Функция y=f(x) называется непрерывной в точке x=x0, если она определена в некоторой окрестности точки x0 (очевидно, и в самой точке x0)и если
∀ε>0,∃δ>0:lx-x0l<δ=>lf(x)-f(x0)l<ε. Функция y=f(x) называется непрерывной в точке x=x0, если она определена в некоторой окрестности точки x0 (очевидно, и в самой точке x0)и если  или,что то же самое
или,что то же самое 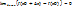 Функция y=f(x) называется непрерывной на данном промежутке, если она непрерывна в каждой точке этого промежутка.
Функция y=f(x) называется непрерывной на данном промежутке, если она непрерывна в каждой точке этого промежутка.
24. Непрерывность сложной функции.
y=f(𝛗(t)), φ(t = x.
Теорема.
1)Если ф-ия φ(t) непрер.в точке t0
|
|
|
2)Ф-ия f(x) непрер.в т. x=x0
Причем φ(t0)=x0.=> то y = f(φ(t))- непрер.в точке t=t0
25) Арифм.оперции над непрерывными ф-ми. Теорема. Пусть ф-ии f(x) и g(x) определены в области Д и непрерывны в точке х0 пранадлежащей области Д, тогда в этой точке неррерывны f(x)±g(x), g(x)*f(x), f(x)/g(x) при условии что g(x0)≠0.
26) Непрерывные элементарные ф-ии.Пример. Ф-ии, которые получаются из осоновных, с помощью конечного числа арифметическимх операций, а так же конечного числа суперпозиции наз-ся элементарными функциями.
Предел показ-степенной ф-ии. Непрерывная ф-ия.
y = f(x), x0 Î D(f) Функция f(x), определенная в некоторой окрестности точки х0, называется непрерывной в этой точке, если предел функции в точке x0 существует и равен значению в этой точке: lim f(x) = f(x0)
28. Односторонняя непрерывность. Точки разрыва и их классификация. Точка x=x0 называется точкой разрыва функции y=f(x), если эта функция не является непрерывной в этой точке.Точка x=x0 называется точкой разрыва первого рода, если в этой точке существует предел слева и справа от этой функции.Точка x=x0 называется точкой разрыва второго рода, если хотя бы один из пределов слева и справа не существует.
Одностр.непрер. В определении непрер.ф-ии в точке x0 требуется существование  и неравенство
и неравенство  . С применением односторонних пределов определ.понятие непрерывности ф-ции в точке слева и справа: Ф-ия наз-ся непрер.в точке х0 слева, если: ∋f(x0-0)=
. С применением односторонних пределов определ.понятие непрерывности ф-ции в точке слева и справа: Ф-ия наз-ся непрер.в точке х0 слева, если: ∋f(x0-0)=  f(x)=f(x0). Ф-ия f(x) наз-ся непрер.в рочке х0 справа, если:: ∋f(x0+0)=
f(x)=f(x0). Ф-ия f(x) наз-ся непрер.в рочке х0 справа, если:: ∋f(x0+0)=  f(x)=f(x0)
f(x)=f(x0)
Св-ва ф-ции непрерывной на отрезке а;б 1) Сохранение знака. 2)Первая и вторая теорема Больцмана-Коши. 3) Ограниченность ф-ции.1 и 2 теоремы Вейерштрасса. Теорема об обратной ф-ции.
Сохранения знака: Если f(x) непр. в т-ке х0 и f(x0)¹0 то $ окрестность этой т-ки в которой ф-ция принимает тот же знак что и знак х0.
Непрер.на отрезке.
Пусть теперь [a;b] (замкнутый) отрезок в D(f). Назовём функциюf(x) непрерывной на отрезке[a;b], если f непрерывна на интервале (a;b), непрерывна справа в точке a и непрерывна слева в точке b, то есть 1) ∀x0∈(a;b)∋  2) ∋
2) ∋  3)
3)  .
.
|
|
|
Теорема Вейерштрасса. Из любой огран.послед.можно выделить сходящиеся подпослед. 1) {xn} безчисл.мн-во одинаковых членов 2) {xn} имеется безчисл.мн-во разл.членов. 1) хотя бы один из членов {xn}повтор.безчисл.кол-во раз. xn1=xn2=…=xnk-сход.послед.
30. Понятие равномерной непрерывности. Функция f (x) называется равномерно-непрерывной на данном множестве, если для всякого? > 0 можно найти такое? =?(?) > 0, что |f (x1) — f (x2)|x1 и x2 из данного множества, удовлетворяющей условию |x1—x2|<? (ср. Непрерывная функция). Например, функция f (x) = x2 равномерно непрерывна на отрезке, равномерно непрерывна на этом отрезке (теорема Кантора). Для интервала эта теорема может не иметь места.
31) Комплексные чи́сла[ — расширение множества вещественных чисел, обычно обозначается. Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица, то есть число, удовлетворяющее уравнению i2 = − 1.
|
|
|


