Дифференцированное функционирование заданий

Статистические процедуры. В качестве одного из аспектов исследования необъективности тестов в отношении групп меньшинств все большее внимание привлекает анализ «систематической ошибки задания» (item bias). Предметом такого анализа является, по существу, относительная трудность отдельных заданий теста для групп, различающихся культурными истоками и жизненным опытом. В психометрической терминологии эта область анализа заданий известна под названием дифференцированного функционирования заданий (сокращенно DIF — по первым буквам differential item functioning). Цель анализа DIF — идентифицировать задания, в отношении которых одинаково способные лица из различных культурных групп имеют разные вероятности успеха. Он основан на предположении, что одинаковая способность означает равенство в отношении конструкта, для оценки которого предназначен данный тест, или критериального поведения, для предсказания которого этот тест используется. Для идентификации таких дифференцированно функционирующих заданий было разработано множество методов, включая статистические и оценочные процедуры (Berk, 1982; Camilli, & Shepard, 1994; Hambleton, & Rogers, 1989; P. W. Holland, & Thayer, 1988; P. W. Holland, & Wainer, 1993; Osterlind, 1983; C. R. Reynolds, & Brown, 1984).

Главная проблема заключается в том, что демографические (или другие связанные с жизненным опытом) различия групп в трудности задания тесно связаны со средне-групповыми различиями в уровне выполнения теста в целом. В результате, задания, обладающие хорошей различительной способностью с точки зрения суммарного показателя, могут выглядеть «необъективными» и, вследствие этого, отбрасываться. Для контроля за такими различиями в суммарном показателе использовалось несколько процедур. С расширением доступа к компьютерам одним из самых многообещающих становится метод, основанный на теории «задание — ответ» (IRT). Этот класс процедур особенно уместно применять в тех случаях, когда в распоряжении исследователей оказываются большие выборки. Как уже было показано в этой главе, характеристические кривые (ICC) для каждого задания показывают вероятность правильного ответа относительно шкалы способности теста (рис. 7-6). Сравнивая /СС для одного и того же задания в любых двух группах, мы можем идентифицировать задания со значимым дифференцированным функционированием относительно полного выполнения теста группами, выраженного в единой шкале. Рис. 7-7 иллюстрирует существо такого сравнения на примере двух заданий. Как легко заметить, для задания 1 характеристические кривые в группах АиВ существенно различаются, тогда как для задания 2 °ни очень похожи. Для каждого задания область между двумя ICC можно использо-^ть, чтобы установить диапазон способности, в котором содержатся признаки DIF. ^хЬсле того как DIF задания идентифицированы, какая бы процедура для этого ни

222

Часть 2. Технические и методологические принципы

использовалась, следующий шаг — выяснение характера и источника установленного различия. Ответ на этот вопрос определяет, войдет ли оно в состав теста или будет отброшено. Для этой цели могут потребоваться различные оценочные процедуры (judgmental procedures), возможно в сочетании с последующим статистическим анализом.

Оценочные процедуры. Не существует какого-то одного, «наилучшего метода» анализа заданий, подходящего для всех целей. Поскольку разные методы дают в чем-то различные виды информации, желательно использовать их комбинацию. Целесообразное сочетание методов зависит от предполагаемого назначения теста и от характера выводов, делаемых из его показателей. Обычно, наилучшим оказывается некоторое сочетание статистических и оценочных процедур.

При правильном применении оценочные процедуры могут снабжать нас полезной информацией, которую невозможно получить иным способом (Scheuneman, 1982; Tittle, 1982). Анализ субъективных оценок особенно полезен на начальном и заключительном этапах конструирования теста, предваряя и завершая статистический анализ. На начальном этапе разработки теста оценочный анализ обычно проводится для того, чтобы отсеять содержание, которое может оскорблять или унижать меньшинства, либо укреплять социальные стереотипы в отношении профессиональных или других социальных ролей. С этой целью крупные издательства тестов регулярно практикуют предварительный просмотр заданий, привлекая к этому как своих сотрудников, так и консультантов со стороны, представляющих разные социокультурные группы (Berk, 1982, chap. 9). Такой просмотр также помогает выявить содержание теста, которое может ограничиваться рамками определенной культуры и потому быть незнакомым для отдельных популяций тестируемых. Следует, однако, заметить, что такие оценочные просмотры, как правило, не дают хороших результатов при предсказании относительной трудности или различительной способности заданий для различных популяций (Plake, 1980; Sandoval, & Miille, 1980; Scheuneman, 1982). Для этой цели необходим статистический анализ эмпирических результатов.

С другой стороны, далеко не все отклоняющиеся от нормы задания, выявленные с помощью статистических процедур, можно расценивать как необъективные. Результаты статистического анализа требуют интерпретации на основе второго просмотра заданий и совершенно иного рода оценочного анализа. На этой стадии задания изучаются на предмет возможных источников их статистической аномальности. Статистические выбросы не обязательно обнаруживают какую-то общую характеристику или явную причину отклонения; каждое задание требует индивидуального рассмотрения. Отдельные выбросы могут просто отражать статистические артефакты, возникающие в результате применения конкретной процедуры. В других случаях отклоняющееся выполнение задания может быть следствием любого из широкого множества условий, которые имеют различные следствия для интерпретации теста. Правильная оценка таких аномальных заданий требует знания как содержательной области теста, так и различий в опыте тестируемых, относящихся к разным популяциям.

Возможная причина аномальности заключается в том, что задание не измеряет один и тот же конструкт в разных группах. Например, словесные аналогии могут измерять вербальное рассуждение в одной группе и знание слов в другой, если такое зада' ние содержит ключевое слово, незнакомое многим членам определенного меньшинства. Подобным же образом арифметическая задача может измерять математическую способность в одной группе и способность понимать сложные словесные формуле

Глава 7. Анализ заданий

223

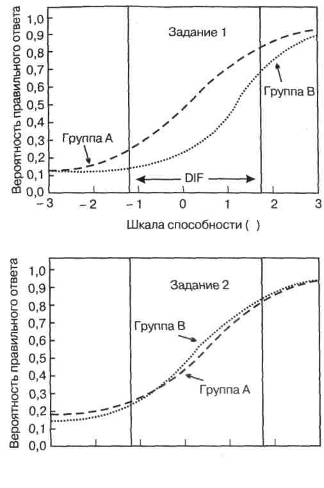
-3  -2-10    1     2    3

Шкала способности ()

Рис. 7-7. Характеристические кривые (ICC) для двух заданий, иллюстрирующие разную степень дифференцированного функционирования задания (DIF) (Графики, с некоторыми упрощениями, взяты из Pashley, 1992. Воспроизведено с разрешения)

ровки в другой. В этих двух примерах недостающие знание не имеет отношения к конструкту, измеряемому тестом в целом. Предположим, однако, что математические задания, включающие десятичные дроби, оказались относительно более трудными Для членов какой-то конкретной группы. Это различие релевантно конструкту математической способности. Следовательно, такие выбросы не являются, в этом смысле, Необъективными заданиями.

В тех случаях, когда аномальные задания идентифицируются статистически, источник этой аномальности можно отчасти прояснить, применяя дополнительные статистические процедуры, такие как анализ ошибочных вариантов ответа, выбираемых ^в задании со множественным выбором. Этот дополнительный анализ заданий, в сочетании с их критическим просмотром и оценкой, должен дать основание для соответствующего действия. Аномальное задание может быть отброшено, пересмотрено це-

224                                                       Часть 2. Технические и методологические принципы

ликом или частично изменено в его некорректной части; возможно, придется расширить или сделать более ясными инструкции к тесту, а может быть, задание будет сохранено в первоначальном виде после его повторного рассмотрения в свете спецификации теста. Анализ задания может даже потребовать переоценки самой этой спецификации, что ведет либо к ее изменению, либо к уточнению допустимых выводов из тестовых показателей.

Известный случай неправильного использования DIF. Широкую огласку получило дело, при рассмотрении которого суд, вероятно, впервые основывался главным образом на анализе заданий в оценке «необъективности теста». Этот прецедент стал известен общественности под названием «дело "Золотого правила"», поскольку оно было связано с проведением экзамена на получение лицензии при найме служащих страховой компанией Golden Rule («Золотое правило»). Сходство между названием компании и общим употреблением этих двух слов в совершенно ином смысле,¹ по-видимому, еще больше осложнило ситуацию. Окончательное решение по данному делу основывалось исключительно на сравнении групповых различий в проценте лиц, справившихся с заданием, без каких-либо попыток установить равенство групп по любому показателю способности, для оценки которой был предназначен тест, или рассмотреть валидность заданий относительно предполагаемой цели теста. Данное решение явно противоречило понятию дифференцированного функционирования задания и, по всей видимости, вело к исключению из теста тех самых заданий, которые были наилучшими предикторами выполнения работы.

Судебной ошибке, содержащейся в решении по делу «Золотого правила», вследствие ее непонимания широкой общественностью и возможного влияния созданного прецедента на использование тестов в профотборе и образовании, были даны критические оценки с разных сторон (например, Lim, & Drasgow, 1990), включая официальное заявление Американской психологической ассоциации.² Это судебное решение также стало темой симпозиума на ежегодном съезде АП А, большая часть докладов на котором впоследствии была опубликована в специальном выпуске журнала Educa - Aional and Psychological Measurement: Issues and Practices (Bond, 1987; Faggen, 1987; Linn, & Drasgow, 1987). Рассмотрение этого печально известного судебного случая высвечивает потенциальные практические опасности для тех, кто пытается оценивать «необъективность теста» по поверхностным и неполным признакам.