 |
Принадлежность точки прямой
|
|
|
|
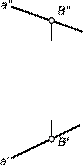Принадлежность точки прямой на комплексном чертеже определяется согласно аксиоме инцидентности, которая устанавливает зависимости и отношения принадлежности между данными элементами евклидова пространства, которая гласит: - если точка B принадлежит прямой a, то проекции точки B` и B" принадлежат одноименным проекциям прямой a` и a" соответственно.
В символической форме эти выражения могут быть записаны
B ∈ a ⇒ B` ∈ a` ∧ B" ∈ a"
Задача на принадлежность точки прямой может быть выражена следующим образом:
- заключить точку B (B`, B") в;
- провести через точку B (B`, B")
прямую a общего положения.
Главные линии плоскости
Среди прямых линий, принадлежащих плоскости, особое значение имеют прямые, занимающие частное положение в пространстве:
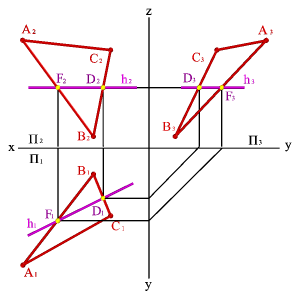
1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (hÎ АВС, h//P1, h2//Ох,h3//Оy)
2.Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (fÎ АВС, f//P2, f1// Ох, f3// Оz).
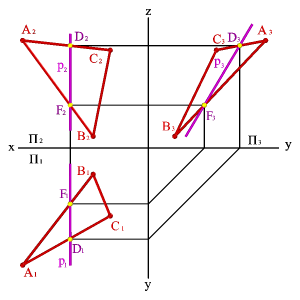
3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проек ций (рÎ АВС, р//P3,р1^ Ох, р2^ Ох).
Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.
4. Прямые, принадлежащие плоскости и образующие с плоскостью проекций наибольший угол называются линиями наибольшего наклона данной плоскости к плоскости проекций. С помощью линий наибольшего наклона определяют двугранные углы между заданной плоскостью и соответствующей плоскостью проекций.
|
|
|
Прямые плоскости, перпендикулярные соответствующим линиям уровня являются линиями наибольшего наклона.
Линия наибольшего наклона к горизонтальной плоскости проекций называется линией ската. Такое название объясняется тем, что эта линия является траекторией, по которой шарик скатывается с данной плоскости. По отношению к плоскостям П2 и П3 целесообразнее употреблять название линия наибольшего наклона.
Линия ската и её горизонтальная проекция образуют линейный угол j, которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций. Горизонтальная проекция линии ската плоскости общего положения перпендикулярна горизонтальной проекции горизонталь этой плоскости. Фронтальная и профильная проекции ската строятся по её принадлежности плоскости.
4. Положение плоскости относительно плоскостей проекции.
В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный aП1; - фронтальный aП2; - профильный aП3).
2.Плоскости, перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:
2.1. Плоскость, перпендикулярная горизонтальной плоскости проекций (a^П1), называется горизонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек этой плоскости совпадают с горизонтальным следом.
|
|
|
2.2. Плоскость, перпендикулярная фронтальной плоскости проекций (a^П2)- фронтально проецирующая плоскость. Фронтальной проекцией плоскости a является прямая линия, совпадающая со следом aП2.
2.3. Плоскость, перпендикулярная профильной плоскости (a^П3) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость.
3. Плоскости, параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельна исследуемая плоскость, различают:
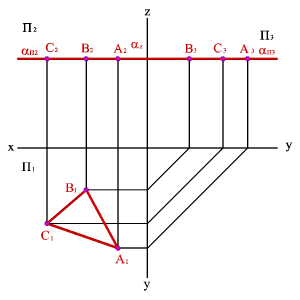
3.1. Горизонтальная плоскость - плоскость, параллельная горизонтальной плоскости проекций (a//П1) - (a^П2,a^П3). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П1 без искажения, а на плоскости П2 и П3 в прямые - следы плоскости aП2 и aП3.
3.2. Фронтальная плоскость - плоскость, параллельная фронтальной плоскости проекций (a//П2), (a^П1, a^П3). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П2 без искажения, а на плоскости П1 и П3 в прямы е - следы плоскости aП1 и aП3.
3.3. Профильная плоскость - плоскость, параллельная профильной плоскости проекций (a//П3), (a^П1, a^П2). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П 3 без искажения, а на плоскости П1 и П2 в прямые - следы плоскости aП1 и aП2.
5. Методы проецирования.
Метод проецирования заключается в том, что любая из точек множества точек пространства может быть спроецирована с помощью проецирующих лучей на любую поверхность. Для этого представим некоторую заданную поверхность (рис.1) и точку А в пространстве. При проведении луча S через точку А в направлении поверхности последний пересечет ее в точке А1. Точку А называют проецируемой точкой. Плоскость α, на которой получают проекцию, называют плоскость проекций. Точка пересечения луча с плоскостью называется проекцией точки А. Прямая АА1 (луч), называется проецирующи м лучом.
Центральное проецирование
Центральный (конический или полярный) метод проецирования основан на том, что при проецировании на плоскость ряда точек (А, B, C и т.д.) все проецирующие лучи проходят через одну точку, называемую центром проецирования, или полюсом.
|
|
|
Представим в пространстве треугольник АВС и проецирующие лучи, проходящие через данный полюс S и через точки АВС треугольника, проведенные до пересечения с плоскостью α. Треугольник А1B1C1 будет центральной проекцией треугольника АВС.
Метод центрального проецирования не удовлетворяет целому ряду условий, необходимых для технического чертежа, а именно: не дает однотипности изображения, полной ясности всех геометрических форм, не обладает удобоизмеримостью, не имеет простоты изображения.
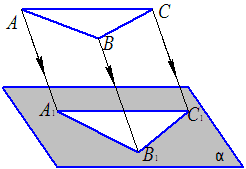Параллельное проецирование
Метод параллельного (косоугольного) проецирования заключается в том, что все проецирующие лучи, проходящие через точки треугольника АВС, будут параллельны между собой. Этот метод вытекает из метода центрального проецирования, при этом полюс должен быть удален на бесконечно большое расстояние от плоскости, на которую проецируется предмет.
|
|
|
