Свойства ортогонального проецирования

 

Наряду со свойствами параллельного (косоугольного) проецирования ортогональное проецирование имеет следующие свойства.

 

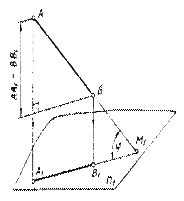
1. Отрезок прямой в общем случае равен гипотенузе прямоугольного треугольника, у которого один катет равен его проекции на данную плоскость проекции, а второй - разности расстоянии концов отрезка до этой плоскости (рис.).

 

2. Любой отрезок прямой и плоская фигура, параллельные плоскости проекций, проецируются на эту плоскость без искажения (рис.), например, если АВ ½½ П ₁, то ½ A ₁ B ₁ ½ = ½ AB ½; D ABC ½½ П ₁, то D A ₁ B ₁ C ₁ = D ABC.

 

 

3. Проекция любой фигуры (плоской фигуры, отрезка прямой и т.д.) не может быть больше самой фигуры (как следствие п. 1 и 2).

4. Ортогональные проекции двух взаимно перпендикулярных прямых, одна из которых параллельна плоскости проекций, а другая не перпендикулярна ей, взаимно перпендикулярны, т.е., если a ^ b, и a ½½ П ₁, то a ₁ ^ b ₁ (рис.).
Пусть дано a ^ b. Построим проекцию a ^ b на П ₁. AA ₁ ^ П ₁ (как проецирующий луч), следовательно, плоскость Г (AA ₁ Ç b) также перпендикулярна П ₁. Прямая а перпендикулярна плоскости Г, так как она перпендикулярна двум прямым AA ₁ и b, принадлежащим плоскости Г. Но a ₁ ½½ a (a ½½ П ₁) и, следовательно, a ^ Г, откуда A ₁ перпендикулярна любой прямой плоскости Г, в том числе и b ₁. Отсюда справедливо, что a ₁ ^ b ₁.
Это доказательство относится как к пересекающимся прямым, так и к скрещивающимся. Как видно из чертежа, если с Ì Г, а Г ^ Q, то c ₁ ^ a ₁.

 

 

7. Эпюр МОНЖА или комплексный чертёж.

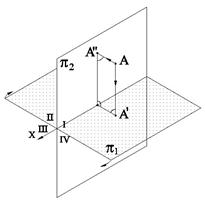
Чертежи в начертательной геометрии строятся главным образом на основании операции ортогонального, то есть прямоугольного, проецирования на две взаимно перпендикулярные плоскости проекций: фронтальную и горизонтальную плоскости. Полученные таким образом два изображения позволяют однозначно определять положение того или иного геометрического образа (фигуры) в пространстве. (рис.).

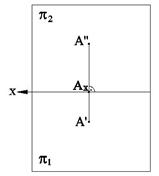Путем вращения одной из этих плоскостей проекций вокруг линии пересечения - оси х, до совмещения в единую плоскость получается плоское изображение, которое называют эпюром Гаспара Монжа или комплексным чертежом. Покажем это на примере изображения точки А (рис.). Плоскости p₁ и p₂ делят пространство на четыре четверти, отмеченные римскими цифрами.

 

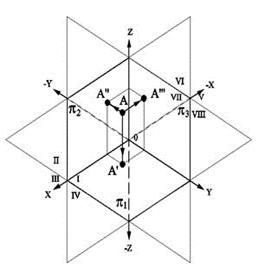
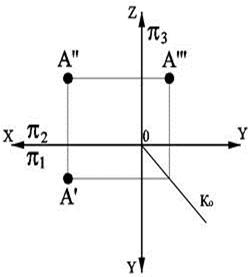Иногда бывает необходимо ввести третью плоскость проекций p₃, перпендикулярную к первым двум плоскостям проекций. Такие три плоскости разделят пространство на восемь частей, называемых октантами. Их нумерация показана на рис.

 

 

8. Прямые общего и частного положения.

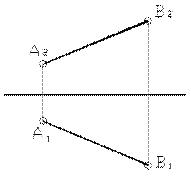
Прямой общего положения называется прямая, которая не параллельна и не перпендикулярна ни одной из плоскости проекций. Пример такой прямой изображён на рисунке 8. Комплексный чертёж этой прямой будет выглядеть следующим образом.

 

 

Прямые частного положения – это прямые, занимающие по отношению к плоскостям проекций особое положение, т.е. либо параллельные, либо перпендикулярные плоскостям проекций.

Первый подкласс прямых частного положения – прямые уровня. Это прямые, параллельные какой-либо плоскости проекций.

Горизонталь – прямая параллельная горизонтальной плоскости П1. Комплексный чертёж такой прямой изображён на рисунке 10.

 

 

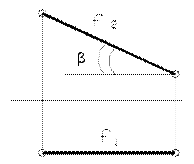
Фронтальная проекция горизонтали всегда параллельна прямой Х, а угол между осью Х и горизонтальной проекцией горизонтали составляет угол между прямой и фронтальной плоскостью проекций. Символическая запись: h // П1; α = Ðh П2.

Фронталь – прямая параллельная фронтальной плоскости П2. Комплексный чертёж фронтали изображён на рисунке 11.

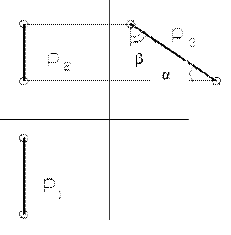
Горизонтальная проекция фронтали параллельна оси Х, а угол β - угол наклона фронтали к горизонтальной плоскости проекций; f₂ // П2, β=Ðf1 П1.

 

Профильная прямая – это прямая, параллельная профильной плоскости П₃. Комплексный чертёж профильной прямой изображён на рисунке 12. Горизонтальная и фронтальная проекции профильной прямой перпендикулярны оси Х, а углы α и β - соответственно, углы наклона прямой к плоскостям П₁ и П2.

 

Истинная величина прямых уровня или, так называемая натуральная величина, отображена на тех плоскостях, которым параллельны эти прямые.

Второй подкласс прямых частного положения – проецирующие прямые. Это прямые, перпендикулярные какой-либо плоскости проекций. К таким прямым относятся: горизонтально–проецирующая, фронтально-проецирующая и профильно-проецирующая прямые.

Их комплексные чертежи изображены соответственно на рисунке (а, б, в).

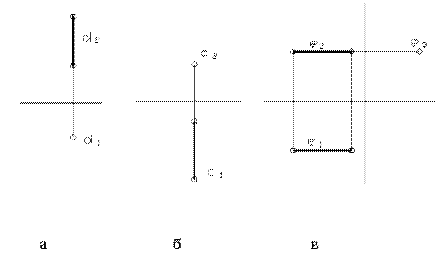
Натуральная величина горизонтально-проецирующей прямой – её фронтальная проекция, фронтально-проецирующей прямой – её горизонтальная проекция, а профильно-проецирующей прямой – её горизонтальная и фронтальная проекции.

 

9. Взаимное положение плоскостей. Взаимное положение прямой и плоскости.

 

Известны три варианта взаимного расположения прямой и плоскости:

1. Прямая принадлежит плоскости.

 

Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.

Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.

Проиллюстрируем примерами использование этих аксиом.

Задача. Дана плоскость (n,k) и одна проекция прямой m₂ (рис.53).

Требуется найти недостающие проекции прямой m, если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k.

Проекция прямой m₂ пересекает проекции прямых n₂ и k₂ в точках В₂ и С₂ соответственно. Для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек, лежащих на прямых n и k соответственно.

Таким образом, точки В и С принадлежат плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит, согласно аксиоме 1, прямая принадлежит этой плоскости.

 

Задача. Через точку В провести прямую m, если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k (рис.).

Пусть точка В принадлежит прямой n, лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В₂ проведем проекцию прямой m₂ параллельно прямой k₂, для нахождения недостающих проекций прямой необходимо построить проекцию точки В₁, как точки лежащей на проекции прямой n₁ и через неё провести проекцию прямой m₁ параллельно проекции k₁.

Таким образом, точка В принадлежит плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме 2 прямая принадлежит этой плоскости.

 

2. Прямая параллельна плоскости.

При решении вопроса о параллельности прямой линии и плоскости необходимо опираться на известное положение стереометрии: прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости и не принадлежит этой плоскости.

Задача. Дано: плоскость общего положения ABC и прямая общего положения а.

Требуется оценить их взаимное положение (рис.).

 

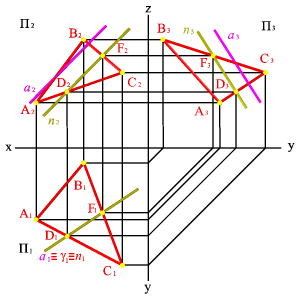Для этого через прямую а проведем вспомогательную секущую плоскость g - в данном случае горизонтально проецирующая плоскость. Найдем линию пересечения плоскостей g и АВС - прямую п (DF).Проекция прямой п на горизонтальную плоскость проекций совпадает с проекцией а₁ и со следом плоскости g. Проекция прямой п₂ параллельна а₂, п₃ параллельна а₃, следовательно, прямая а параллельна плоскости AВС.

 

3. Прямая пересекает плоскость.

Нахождение точки пересечения прямой линии и плоскости – одна из основных задач начертательной геометрии.

Задача. Дано: плоскость AВС и прямая а.

Требуется найти точку пересечения прямой с плоскостью и определить видимость прямой по отношению к плоскости.

Алгоритм решения задачи (рис.):

1. 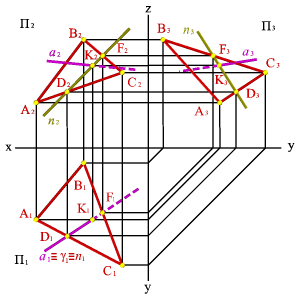Через горизонтальную проекцию прямой а₁ проведем вспомогательную горизонтально проецирующую плоскость g (таким образом а Î g).

2. Находим линию пересечения вспомогательной плоскости с заданной. Горизонтальный след плоскости g₁ пересекает проекцию плоскости A₁В₁С₁ в точках D₁ и F₁, которые определяют положение горизонтальной проекции п₁ - линии пересечения плоскостей g и AВС. Для нахождения фронтальной и профильной проекции п спроецируем точки D и F на фронтальную и профильную плоскости проекций.

3. Определяем точку пересечения прямых а и п. На фронтальной и профильной проекциях линия пересечения плоскостей п пересекает проекции а в точке К, которая и является проекцией точки пересечения прямой а с плоскостью AВС, по линии связи находим горизонтальную проекцию К₁.

4. Методом конкурирующих точек определяем видимость прямой а по отношению к плоскости AВС.

 

10. Пересечение двух плоскостей. Частные случаи.

 

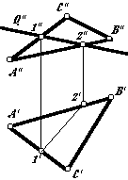
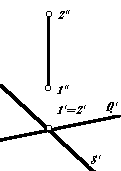Пересечение проецирующей прямой с плоскостью общего положения

а) решается на основе: прямая пересечения двух плоскостей может быть определена двумя точкам и, поэтому взяв на не вырожденной плоскости две произвольные прямые определим две точки в пересечении с вырожденной проекцией прямой

Пересечение двух проецирующих плоскостей на одну и ту же координатную плоскость определяется из условия пересечения их вырожденных. Линия пересечения 1-2 будет проецирующей в точку пересечения вырожденных проекций

 

11. Пересечение прямой с плоскостью. Алгоритм определения точки пересечения прямой
с плоскостью. Частные случаи.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: