Классификация поверхностей. Задание поверхности на комплексном чертеже.

Поверхности разделяют:

o По закону образования - на закономерные и незакономерные.
Закономерные задаются графически и аналитически, незакономерные - только графически.

o По признаку развёртывания в плоскость - развёртывающиеся и неразвёртывающиеся.

o По форме образующей:
- с прямолинейными образующими - линейчатые поверхности;
- с криволинейной образующей - кривые поверхности.

o По способу перемещения образующей:
- с поступательным движением образующей;
- с вращательным движением образующей - поверхности вращения;
- с движением образующей по винтовой линии - винтовые поверхности.

 

 

Поверхности на комплексном чертеже могут быть заданы:

o Проекциями направляющих и способом перемещения по ним образующих.

o Семейством линий, принадлежащих поверхности - каркасный способ задания поверхности.

o Очерком поверхности, т.е. линиями, ограничивающими на комплексном чертеже область существования проекций.

2. Линейчатые поверхности:

Линейчатая поверхность в общем случае однозначно определяется тремя направляющими линиями, т.е. при перемещении по ним образующей.

Линейчатые поверхности делятся на развёртывающиеся и неразвёртывающиеся.

К развёртывающимся относятся: цилиндрические поверхности, конические поверхности, поверхности с ребром возврата (торса), призматические поверхности, пирамидальные поверхности.

 

Цилиндрическая поверхность.

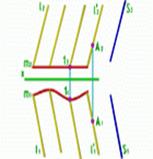Цилиндрическая поверхность образуется перемещением прямолинейной образующей l по криволинейной направляющей m, причём образующая l остаётся постоянно параллельной заданной направляющей S.

 

 

2.2 Коническая поверхность.

Коническая поверхность получается при движении прямолинейной образующей l по криволинейной направляющей m, причём образующая l постоянно проходит через неподвижную точку S.

Цилиндроид, коноид, косая плоскость.

Неразвёртывающиеся линейчатые поверхности - это поверхности с плоскостью параллелизма.

Цилиндроид - образуется движением по двум криволинейным направляющим m и n прямолинейной образующей l, остающейся всё время параллельной плоскости параллелизма.

Рассмотрим построение проекций точки и линии последовательно на перечисленных выше поверхностях вращения.

 

Цилиндр

 

Пусть задан прямой цилиндр, плоскости основания которого параллельны плоскости П ₁(рис.).

Решим задачу. Зная фронтальные проекции точек А и В, лежащих на боковой поверхности цилиндра, построить отсутствующие проекции. Поскольку на П ₁ боковая поверхность цилиндра проецируется в окружность, то А ₁ и В ₁ лежат, очевидно, на ней. Их положение находим по вертикальным линиям связи.

Профильные проекции А ₃, В ₃ лежат, как известно, на горизонтальных линиях связи с фронтальными проекциями А ₂ и В ₂. При этом, в соответствии с правилами ортогонального проецирования, расстояние от Ф₃ до профильной проекции точки равно расстоянию от Ф₁ до горизонтальной проекции точки. Причем точка В ₃ – невидимая, так как лежит на невидимой части боковой поверхности цилиндра.

Решим следующую задачу: по заданной фронтальной проекции А₂В₂ линии (рис.) построим отсутствующие проекции.

Горизонтальная проекция А₁В₁ совпадает с окружностью, так как все точки линии АВ лежат на боковой поверхности цилиндра.

При построении профильной проекции А₃В₃ следует иметь в виду, что линия АВ пересекает прямую СD, которая на П₃ является контуром С₃D₃цилиндра. Поэтому сначала следует определить положение контурной точки 1₃, а затем соединить точки А₃ и В₃ линией, которая в отличии от А₂1₂В₂не является прямой. В связи с этим для построения необходимо на А₂1₂В₂ выбрать несколько промежуточных точек (2₂, 3₂ и т.д.) и построить их профильные проекции (2₃, 3₃ и т.д.), руководствуясь вышеуказанным правилом взаимосвязи горизонтальной и профильной проекций. Чем большее количество промежуточных точек выбираем, тем более точными будут построения.

Конус

 

Решим те же задачи построения проекций точки и линии, лежащих на поверхности конуса (рис.).

 

Построим отсутствующие проекции точек А и В, расположенных на поверхности прямого кругового конуса, если известно положение А ₂ и В ₂.

Для построение горизонтальной проекции точки, например А, необходимо через ее фронтальную проекцию провести горизонтальную линию. Тогда на П ₁ эта линия 12 представляет собой дугу окружности диаметром 1₂2₂=1₁2₁. По линии связи на ней находим А ₁. Аналогично, проводя дугу окружности радиусом S ₁3₁, равным расстоянию от оси конуса до точки 3₂ на его контуре, определяем положение на ней точки В ₁. По этим проекциям находим положение А ₃, В ₃.

По известной проекции А ₂ В ₂ линии на поверхности конуса построить горизонтальную и профильную.

Выбрав на линии А ₂ В ₂ промежуточную точку 4₂, найдем 4₁ так же, как сделали это для точек А и В. Соединив точки А ₁, 4₁, В ₁, получим горизонтальную проекцию линии АВ.

Для построения профильной проекции А ₃ В ₃ необходимо найти положение контурной точки 4, лежащей на SA. По фронтальной проекции 4₂, лежащей на S ₂ A ₂, находим профильную проекцию 4₃, лежащую на S ₃ A ₃. Теперь точки А ₃, 4₃, В ₃ можно соединить линией.

При соединении точек линией всегда надо руководствоваться достаточно очевидным правилом: на каждой проекции точки, принадлежащие линии, следует соединять в одинаковой последовательности. Так, если на фронтальной проекции точка 4 является промежуточной, то она будет промежуточной и на других проекциях.

 

 

Сфера

 

Проекцией сферы на любую плоскость проекций является окружность.

Рассмотрим построение проекций точек на поверхности сферы (рис. 4.6). Задача состоит в том, чтобы по известным проекциям построить отсутствующие. Для упрощения решения необходимо все характерные точки сферы обозначить. Точки, лежащие на экваторе, обозначим через А, В, С, D; точки, лежащие на главном меридиане – А, Е, С, F. Очевидно, что точки А и С принадлежат одновременно и экватору, и главному меридиану.

 

При построении проекций следует иметь ввиду, что любая параллель на П ₂ проецируется в горизонтальную прямую, а на П ₁ в окружность.

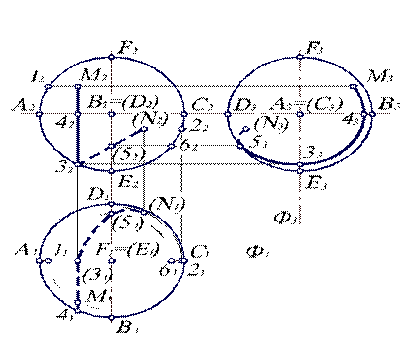Пусть задана фронтальная проекция точки М. Проведем через нее параллель. Тогда на П ₂ получим горизонтальную прямую, проходящую через точку М ₂. А на П ₁ – дугу окрудности радиусом F ₁1₁, равным расстоянию от вертикальной оси до токи 1₂. Ясно, что точка М ₁ лежит на этой окружности. По двум проекциям М ₁ и М ₂, используя правило взаимосвязи проекций, построим М ₃.

Рассмотрим другую точку N, проекция которой N ₂ на П ₂ является невидимой. Аналогично предыдущему построим N ₁, лежащую на дуге окружности радиусом F ₁2₁. Так как N ₂ - невидимая, то N ₁ лежит выше оси Ф₁. А поскольку точка N находится на поверхности нижнего полушария, что видно из положения N ₂, то N ₁ - невидимая. Профильная проекция N ₃ строится по известному правилу взаимосвязи проекций. При этом, так как N ₁ лежит выше оси Ф₁, то N ₃ - левее Ф₃. Поскольку точка N лежит в правом полушарии, то на П ₃ она невидимая, так как на П ₃ все правое полушарие закрыто от нас левым и является невидимым.

Видимость и невидимость полушарий, а следовательно, и точек, лежащих на них, можно легко определить, рассматривая с разных точек зрения обыкновенный резиновый мячик, нарисовав на нем экватор и два меридиана, расположенных в плоскостях, перпендикулярных друг другу.

Построим горизонтальную и профильную проекции линии МN, если известна ее фронтальная проекция М ₂ N ₂, состоящую из прямолинейных отрезков М ₂3₂ и 3₂ N ₂.

Очевидно, что точка 3₁ лежит на А ₁ Е ₁, так как 3₂ - на А ₂ Е ₂. При этом прямая МN проходит через экватор (точка 4₂). Следовательно, на П ₁ – через точку 4₁. А участок 4₁3₁ – невидимый, поскольку, как видно по его фронтальной проекции 4₂3₂, он лежит в нижнем полушарии, т.е. ниже экватора.

Для построения проекций участка 3 N выберем промежуточную точку 5₂. Тогда точка 5₁ лежит на дуге окружности радиуса 5₂6₂. Соединив точки 3₁, 5₁, N ₁, получим искомую линию М ₁4₁3₁5₁ N ₁.

Построим профильную проекцию М ₃ N ₃, которая проходит через те же промежуточные точки. Так как М ₂3₂ – вертикальная прямая, то на П ₃ она представляет собой дугу М ₃3₃ окружности радиуса 4₂3₂=А₃3₃. Точка 5₃ – контурная для профильной проекции сферы. Значит, остается соединить точки 3₃, 5₃, N₃ кривой линией. При этом участок 5₃ N ₃ – невидимый.

Если в нашу задачу входит более точное построение проекций линии MN, тогда на всех участках, где ее проекции не являются отрезками прямой или окружности, необходимо выбрать несколько промежуточных точек.

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: