Построения сечения конической поверхности плоскостью.

 

Рисунок – Построение пересечения конической поверхности плоскостью

Пусть задана секущая проецирующая плоскость σ⊥π₂ (Рисунок). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.

1. Построим характерные точки. Это точки, лежащие на крайних образующих и на окружности основания конуса (1, 2, 3). Их проекции строятся по линиям проекционной связи.

2. 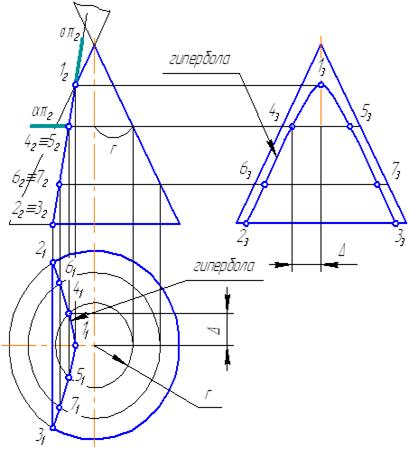Для построения промежуточных точек, воспользуемся методом вспомогательных секущих плоскостей. Введём плоскость α⊥π₂ и перпендикулярно оси вращения, что даст в сечении окружность радиусом r. Строим эту окружность на π₁. Плоскость α пересекает и заданную плоскость сечения по прямой, проекции которой на π₁ и π₃ совпадают с линиями проекционной связи.

3. На пересечении этих двух сечений на плоскости проекций π₁ строим точки 4, 5. Профильные проекции этих точек строим по линии проекционной связи, откладывая расстояние от оси вращения конуса, равное Δ.

4. Аналогично строим точки 6, 7. Плавно соединим построенные точки, образуя гиперболу.

5. Обведём то, что осталось от конуса после такого среза с определением видимости. В нашем примере все проекции построенной кривой будут видимы.

 

20. Аксонометрические проекции. Изометрическая проекция

 

Для тoгo чтобы получить аксонометрическую проекцию пред­мета (рис. 106), необходимо мысленно: поместить предмет в сис­тему координат; выбрать аксонометрическую плоскость проекций и расположить предмет перед ней; выбрать направление парал­лельных проецирующих лучей, которое не должно совпадать ни с одной из аксонометрических осей; направить проецирующие лучи через все точки предмета и координатные оси до пересечения с аксонометрической плоскостью проекций, получив тем самым изображение проецируемого предмета и координатных осей. На аксонометрической плоскости проекций получают изобра­жение — аксонометрическую проекцию предмета, а также про­екции осей систем координат, которые называют аксонометриче­скими осями. Аксонометрической проекцией называется изображение, по­лученное на аксонометрической плоскости в результате парал­лельного проецирования предмета вместе с системой координат, которое наглядно отображает его форму. 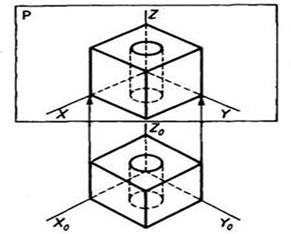Система координат состоит из трех взаимно пересекающихся плоскостей, которые имеют фиксированную точку — начало координат (точку О) и три оси (X, У, Z), исходящие из нее и расположенные под прямым углом друг к другу. Сис­тема координат позволяет производить измерения по осям, определяя положение предметов в пространстве.

 

 

Можно получить множество аксонометрических проекций, по- разному располагая предмет перед плоскостью и выбирая при этом различное направление проецирующих лучей (рис. 107).

Наиболее употребляемой является так называемая прямо­угольная изометрическая проекция (в дальнейшем будем использовать ее сокращенное название — изометрическая проек­ция). Изометрической проекцией (см. рис. 107, а) называется та­кая проекция, у которой коэффициенты искажения по всем трем осям равны, а углы между аксонометрическими осями составляют 120°. Изометрическая проекция получается с помощью па­раллельного проецирования.

 

22. Взаимная параллельность прямых и плоскостей.

 

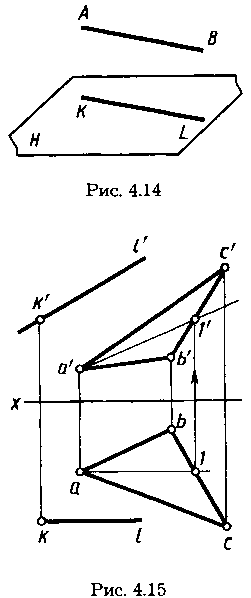Построение взаимно параллельных прямой линии и плоскости. Известно, что если прямая линия (АВ, рис. 4.14) параллельна прямой KL, лежащей в плоскости, то она параллельна этой плоскости.

Для построения прямой, проходящей через заданную точку пространства параллельно заданной плоскости, достаточно провести прямую, параллельную любой прямой, принадлежащей плоскости.

При этом возможно бесчисленное множество решений. Дополнительные требования могут обусловить единственное решение.

В качестве примера на рисунке 4.15 показано построение проекций прямой линии, проходящей через точку с проекциями к’, к, параллельной плоскости треугольника с проекциями a'b'c', abc и параллельной плоскости V — дополнительное требование. В плоскости треугольника проведена фронталь с проекциями а'1', а—1. Проекции искомой прямой проведены через проекции к’, к точки параллельно проекциям фронтали к'l' || а'l', kl || а—1.

Для того чтобы проверить, параллельна ли прямая заданной плоскости, можно попробовать провести в этой плоскости прямую, параллельную заданной. Если такую прямую в плоскости построить не удается, то заданные прямая и плоскость не параллельны между собой. Можно также попытаться найти точку пересечения данной прямой с данной плоскостью. Если такая точка не может быть найдена, то заданные прямая и плоскость взаимно параллельны.

 

Построение взаимно параллельных плоскостей. Для такого построения используют известное свойство: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны. Так, например, на рисунке 4.16, а построена плоскость, проходящая через точку с проекциями к’, к, параллельная плоскости, заданной проекциями a'b', ab и а'с', ас пересекающихся прямых. Для этого через фронтальную проекцию к' проведены фронтальные проекции d'k' || а'с', е'к' || a'b' и через горизонтальную проекцию к - горизонтальные проекции dk || ас, ек || ab. Построенная плоскость, определяемая проекциями k'd ', к'е' и kd, ке, будет параллельна заданной плоскости.

Построение параллельных плоскостей на чертеже удобно выполнять с помощью главных линий плоскости — горизонталей и фронталей. На рисунке 4.16, б плоскость Р задана проекциями a'b', c'd' и ab, cd параллельных прямых. Параллельная ей плоскость Т должна проходить через точку с проекциями к’, к. Проекции плоскости Т построены с помощью фронтальных проекций k’f' фронтали и k'g' горизонтали и горизонтальных проекций kg горизонтали и kf фронтали. При этом k’f’ || 1' З', kg || 1—2.

 

 

23. Способы преобразования комплексного чертежа.

25. Четыре основные задачи на преобразование комплексного чертежа.

Задача №1. Преобразовать комплексный чертеж так, чтобы прямая общего положения АВ оказалась параллельной одной из плоскостей проекций т.е. прямой уровня(горизонталь или фронталь) новой системы.

Для решения задачи необходимо заменить плоскость проекций П₁, или П₂ новой плоскостью проекций П₄, параллельной прямой АВ и перпендикулярной к незаменяемой плоскости проекций. Для того чтобы прямая АВ в новой системе плоскостей проекций стала, например, фронталью, нужно заменить фронтальную плоскость проекций П₂ новой плоскостью П₄ П₁ и параллельной прямой АВ.

Рассмотрим подробно этапы построения на комплексном чертеже (рис. 5.1), необходимые для решения первой основной задачи на преобразование комплексного чертежа:

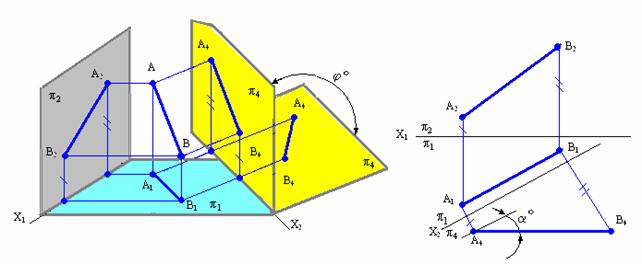
Рис. 5.1. Изображение преобразования прямой общего положения в прямую положения уровня: а - в пространстве; б – на комплексном чертеже

 

1) провести новую ось проекций х₁₄ параллельно А₁В₁ на произвольном расстоянии от нее; такое положение оси х₁₄ обусловливается тем, что П₄ параллельна АВ. В частном случае, если плоскость П₄ проведена непосредственно через прямую АВ, ось х₁₄ = А₁В₁;

2) выбрать на прямой две точки А(А₁А₂) и В(В₁В₂);

3) построить проекции точек А и В на плоскости П₄.

Прямая А₄В₄ является проекцией прямой АВ на плоскость П₄. Прямая AB в новой системе плоскостей проекций П₁/П₄ является фронталью.
Отрезок [АВ] прямой проецируется на плоскость П₄ в истинную величину, т.е. | А₄В₄ | = | АB |, a- величина угла наклона прямой АВ к плоскости П₁.

 

3адача 2. Преобразовать комплексный чертеж так, чтобы линия общего положения АВ стала проецирующей.

.

Рис. 5.2 Преобразование прямой АВ общего положения в горизонтально-проецирующую.

Для решения задачи заменить плоскость П₂ исходной системы П₂/П₁ плоскостью П₄ // А₁В₁, при этом плоскость П₄ будет перпендикулярной П₁ так как АВ // П₄ и образует с ней новую систему плоскостей проекций П₁/П₄.

Построения на комплексном чертеже:

 

1) провести новую ось проекций х₁₄ // А₁В₁;

2) построить проекции точек А и В на плоскости П₄, взяв координаты точек из плоскости П₂;

3) заменить плоскость П₁ на новую П₅, которая будет П₄ и А₄В₄. Для этого нужно провести новую ось проекций х_4,5.

Так как расстояния точек А и В до плоскости П₄ одинаковы, то проекции их на плоскости П₅ совпадут, А₅ ≡ В₅, прямая АВ (А₅В₅) в новой системе плоскостей проекций заняла проецирующее положение и стала горизонтально проецирующей. Прямую общего положения преобразовать в проецирующую заменой только одной плоскости проекций нельзя, так как плоскость П₅ перпендикулярная прямой, не будет перпендикулярна ни одной из «старых» плоскостей проекций, и, следовательно, не сможет образовать ни с одной из них прямоугольной системы плоскостей проекций.

Для того чтобы прямую общего положения преобразовать в проецирующую, необходимо выполнить две последовательные замены плоскостей проекций. Прямую общего положения следует преобразовать в линию уровня, а затем линию уровня преобразовать в проецирующую (рис. 5.2).

 

Задача №3. Преобразовать комплексный чертеж так, чтобы плоскость общего положения стала проецирующей(рис. 5.3).

Для решения задачи необходимо заменить плоскость П₁ или П₂ исходной системы П₂/П₁ новой плоскостью П₄, перпендикулярной плоскости (АВС). Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Следовательно, если какую-либо прямую, принадлежащую плоскости , преобразовать в проецирующую, то плоскость в новой системе плоскостей проекций станет проецирующей.

Проще всего для этой цели воспользоваться линией уровня.

.

Рис. 5.3. Преобразование плоскости общего положения в проецирующую

На чертеже плоскость (АВС) преобразована во фронтально проецирующую (см. рис. 5.3) путем преобразования горизонтали h(h₁,h₂), принадлежащей плоскости, во фронтально- проецирующую прямую. В новой системе плоскостей проекций П₁/П₄ плоскость является фронтально проецирующей ( 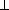4), и поэтому ее проекция на П₄ вырождается в прямую линию ₄ (С₄, А₄, В₄).

α – величина угла наклона плоскости к плоскости П₁.

 

Задача №4. Преобразовать комплексный чертеж так, чтобы плоскость общего положения стала плоскостью уровня (параллельной одной из плоскостей проекций) новой системы.

.

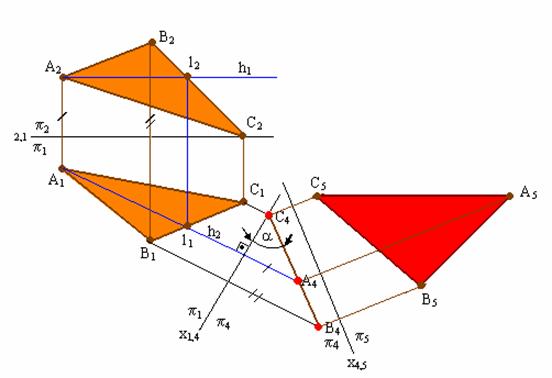
Рис. 5.4. Решение 4-й задачи на преобразование плоскости общего положения в плоскость уровня

Плоскость общего положения преобразовать в плоскость уровня заменой только одной плоскости проекций нельзя, так как плоскость П₄, параллельная ей, не будет перпендикулярна ни одной из старых плоскостей проекций и, следовательно, не образует ни с одной из них прямоугольной системы плоскостей проекций.

Для того чтобы плоскость общего положения преобразовать в плоскость уровня, необходимо выполнить две последовательные замены плоскостей проекций.

Вначале плоскость необходимо преобразовать в проецирующую, т. е. решить задачу 3 на преобразование комплексного чертежа, а затем проецирующую плоскость преобразовать в плоскость уровня. На рис. 5.4 показано преобразование плоскости Δ(АВС) в горизонтальную плоскость уровня.

 

 

Допустим, что заданная плоскость Г является фронтально проецирующей (рис. 5.5). Заменим плоскость П₁ новой плоскостью проекций П₄, параллельной плоскости Г (ΔАВС) и, перпендикулярной незаменяемой плоскости П₂. В новой системе плоскостей проекций П₂/П₄ плоскость Г (АВС) станет горизонтальной плоскостью уровня.

.

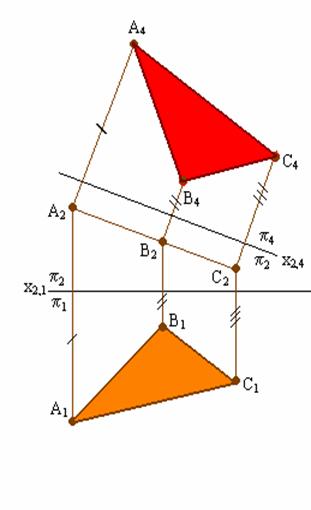
Рис. 5.5. Решение четвертой задачи на преобразование комплексного чертежа

Построения на комплексном чертеже:

 

1) проводим новую ось проекций х₂₄ параллельно А₂С₂ на произвольном от нее расстоянии; такое положение оси проекций х₂₄ обусловливается тем, что П₄параллельна Г (АВС). Ось х₂₄ совпадает с прямой (А₂С₂), если плос- кость П₄ совмещается с плоскостью Г (АВС);

2) построим проекции точек А, В и С на плоскость П₄;

3) треугольник А₄В₄С₄ является проекцией треугольника АВС на плоскость П₄.

Примечание. Так как плоскость треугольника АВС параллельна П_4, значит отображение этого треугольника на П₄ будет в натуральную величину.

В данном конспекте лекций рассматривается только способ замены плоскостей проекций.

 

26. Следы прямой. Следы плоскости.

 

Следы прямой

 

Следами прямой называют точки её пересечения с плоскостями проекций. В зависимости от того, какую плоскость проекций пересекает прямая в данной точке, различают горизонтальный, фронтальный и профильный след.

Прямые, занимающие общее положение, пересекают три плоскости проекций, линии уровня – две, а проецирующие прямые – одну.

Алгоритм построения следов на эпюре

Найдем следы прямой a, заданной отрезком AB. Как видно на рисунке ниже, AB занимает общее положение, поэтому для решения задачи необходимо построить проекции трех точек.

 

1. Горизонтальный след H_a. Продлим фронтальную проекцию прямой a до пересечения с осью X в точке H_a''. Полученная точка – фронтальная проекция горизонтального следа. По линии связи на a' найдем точку H_a'. Она является горизонтальной проекцией горизонтального следа и совпадает с т. H_a.

2. Фронтальный след F_a. Продлим горизонтальную проекцию a' до пересечения с осью X в точке F_a'. Полученная точка – горизонтальная проекция фронтального следа*. По линии связи на прямой a'' найдем точку F_a". Она является фронтальной проекцией фронтального следа и совпадает с т. F_a.

3. Профильный след W_a строится аналогично. Для нахождения двух его проекций, W_a'' и W_a', необходимо продлить a'' и a' до пересечения с осью Z.

 

 

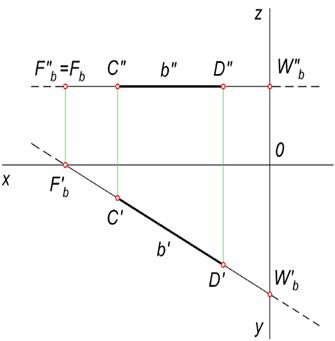
На следующем рисунке показано построение следов горизонтали b​, заданной отрезком CD. Как и другие линии уровня, горизонталь пересекает только две плоскости проекций.

 

Несмотря на то, что рассмотренный нами алгоритм универсален, лучше понять смысл геометрических построений позволяет наглядное изображение прямой в пространстве.

Примечание

* Фронтальный след прямой по определению является точкой, которая лежит во фронтальной плоскости. Её координата Y равна нулю. Из этого следует, что горизонтальная проекция F' фронтального следа находится на оси X.

Следы плоскости

 

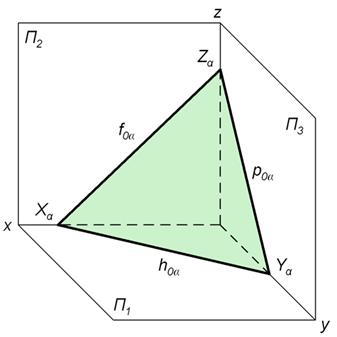На рисунке показана плоскость общего положения α. Она пересекает плоскости проекций П₁, П₂, П₃ по прямым h_0α, f_0α и p_0α. Эти прямые называются горизонтальным, фронтальным и профильным следом плоскости α.

 

Оси координат пл. α пересекает в точках X_α, Y_α и Z_α. Они называются точками схода следов. При этом X_α = h_0α ∩ f_0α, Y_α = h_0α ∩ p_0α, Z_α = f_0α ∩ p_0α. Здесь знак ∩ означает пересечение.

На комплексном чертеже плоскость можно задать проекциями двух её следов. Это обеспечивает наглядность изображения и удобство при выполнении ряда построений. Стоит отметить, что угол, образованный следами плоскости на комплексном чертеже, не равен углу между ними в пространстве.

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: