 |
Геометрическое представление множества допустимых альтернатив
|
|
|
|
Введем в рассмотрение декартову прямоугольную систему координат и условимся откладывать затраты на рекламу на оси абсцисс, а на стимулирование продаж - на оси ординат. В силу не отрицательности рассматриваемых переменных все допустимые альтернативы будут принадлежать первой четверти введенной системы координат.
Изобразим произвольную точку X = (A, S), принадлежащую первой четверти введенной системы координат:

Точка X может рассматриваться как альтернатива ЛПР, поскольку она предусматривает выделение определенной суммы денег на рекламу и стимулирование продаж, однако допустимой альтернативой она будет, если только сумма ее координат A + S не будет превосходить бюджета маркетинга M.
Изобразим все альтернативы (A, S), полностью исчерпывающие бюджет маркетинга (A + S = M):
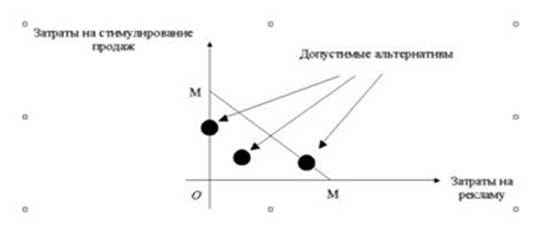
Легко видеть, что каждая точка получившегося треугольника, включая его границы, является допустимой альтернативой ЛПР, поскольку для нее выполняются все сформулированные выше ограничения:
A + S≤ M; A≥ 0; S≥ 0.
Идентификация типа задачи принятия решения
Цель задачи принятия решения порождает критерий, позволяющий упорядочить имеющиеся альтернативы: каждому из имеющихся альтернативных распределений бюджета маркетинга (A,S), сопоставляется величина объема сбыта F(A,S), который будет достигнут при соответствующих затратах на рекламу и стимулирование продаж:
F: (A, S) → F(A, S).
Вывод: Задача инвестора является однокритериальной или полностью определенной задачей принятия решения.
Сравнение альтернатив и выбор решения
Исключение из рассмотрения доминируемых альтернатив
Принято считать (впрочем, с известными оговорками), что увеличение затрат на рекламу и / или стимулирование продаж всегда приводит к увеличению сбыта. Это означает, что все планы, при которых бюджет маркетинга распределяется не полностью (A + S < M), не могут дать максимального сбыта. Исключив эти планы из числа допустимых альтернатив, получим математическую модель, к которой сводится задача распределения бюджета маркетинга:
|
|
|
F(A, S) = 400A1/8 S1/4 → max, A + S = 60, (1)
или, что то же самое, к соотношению
F(A) = 400A1/8 (60 - A)1/4 → max, 0 A 60. (2)
Задача (1) имеет решение в соответствии с теоремой Вейерштрасса, и это решение может достигаться только
либо на границе допустимого множества (A=0, A=60),
либо в точках, в которых производная целевой функции задачи (2) равна нулю или не существует.
Вычислим производную целевой функции задачи (2):
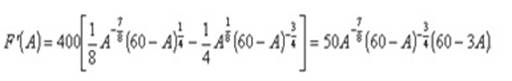
Таким образом, задача (2) не может иметь решения ни в одной точке, за исключением следующих точек:
A1=0, A2=20, A3=60.
Вычисление значения критерия для каждой из допустимых альтернатив
Таким образом, задача (1) может иметь решения только в точках
(A1, S1) = (0, 60), (A2, S2) = (20, 40), (A3, S3) = (60, 0).
Для того, чтобы выбрать решение, найдем соответствующие недоминируемым альтернативам объемы сбыта:

4.3 Выбор решения: Анализ таблицы показывает, что максимальный объем сбыта примерно в 1463 единицы товара достигается при затратах на рекламу в размере $20.000 и на стимулирование продаж в размере $40.000.
Задача
Зависимость между объемом сбыта Q (шт.) некоторого товара, затратами на рекламу A ($1000) и затратами на стимулирование продаж S ($1000) задана функцией
Q = 400A1/4 S1/8.
Рассмотрим проблему распределения бюджета маркетинга M = 120 тысяч долларов между затратами на рекламу A и затратами на стимулирование продаж S.
Уяснение цели принятия решения
Распределить бюджет маркетинга между затратами на рекламу и затратами на стимулирование продаж таким образом, чтобы объем продаж был максимальным.
|
|
|


