Часть I. Локализация точки на шкале (нольмерное шкалирование)

ЧАСТЬ I. ЛОКАЛИЗАЦИЯ ТОЧКИ НА ШКАЛЕ (НОЛЬМЕРНОЕ ШКАЛИРОВАНИЕ)

Глава 1. Методы измерения порогов

 

Исторически сложилось так, что первыми методами психологических измерений были методы, позволяющие определять локализацию точки на психологической шкале. Их появлением мы обязаны Г. Т. Фехнеру, пытавшемуся с их помощью разрешить психофизическую проблему — выяснить закон соответствия психического образа и вызвавшего его физического воздействия. Согласно Фехнеру, через абсолютный порог задается начальная точка отсчета на психологической шкале, а через разностный порог вводится единица измерения на ней.

Под порогом всегда подразумевается некое критическое значение, разделяющее исследуемый ряд явлений на 2 класса. Абсолютный порог — то минимальное значение в континууме стимулов, выше которого раздражитель всегда воспринимается. Разностный порог — то минимальное различие в выраженности определенного физического параметра стимулов, превышение которого приводит к восприятию их различия.

Для решения основной задачи Фехнером была предпринята разработка методов измерения порога. Предложенные им три метода измерения порога добрую сотню лет были единственными методами определения чувствительности и до сих пор признаются классическими. Знакомство с ними и в наши дни составляет основу подготовки психолога-экспериментатора. И дело не только и даже не столько в том, что порог как мера чувствительности — психической способности воспринимать, чувствовать, реагировать — широко используется в различных областях психологических исследований. Главное в другом. Хотя пороговые, как и любые другие психофизические измерения, если их рассматривать в содержательном аспекте, представляют собой частный случай психометрических измерений, в пороговых методах — наиболее простых измерительных процедурах — уже нашли отражение основные трудности количественного определения переменных и способы их преодоления: вариабельность измеряемых величин и использование средних значений для их характеристики; их вероятностный характер, влияние многочисленных и далеко не всегда контролируемых экспериментатором факторов и введение уравновешивающих их действие процедур. Оба указанные качества — простота и характерность — определяют место пороговых методов в курсе обучения. методам психологических измерений.

Развитие методов в науке обычно связано с появлением новых проблем. Главной и единственной задачей классической психофизики было изучение закона соответствия между психическими и физическими переменными. Основное внимание уделялось стимульным переменным, поскольку молчаливо предполагалось отсутствие влияния на ответы испытуемого в эксперименте таких несенсорных факторов как изменение мотивации, получение дополнительной информации об экспериментальной ситуации и т. д. Эти предположения реализовались в процедурных особенностях пороговых измерений и представлениях о пороге как мере чувствительности. Характерной чертой трех классических пороговых методов является довольно большое разнообразие стимулов, применяемых в эксперименте в качестве независимой переменной, и отсутствие какого бы то ни было контроля упомянутых выше несенсорных факторов, фактически всегда включенных в эксперимент. Те статистические показатели, которые приняты в этих методах в качестве пороговых мер, на самом деле являются, строго говоря, мерами исполнения, т. к. определяются не только уровнем чувствительности испытуемого, но и теми несенсорными факторами, которые управляют выбором его ответа. Несмотря на это, такие качества пороговых методов, как простота, меньшие затраты времени на измерение, а также удобство выражения пороговых мер в физических единицах обеспечивают этим методам широкое применение в современной исследовательской практике.

Современная психофизика (в отличие от классической), решая проблему измерения чувствительности, основное внимание уделяет процессу решения сенсорной задачи (выбора испытуемым ответа) в типичной для порогового эксперимента ситуации отсутствия ясных отчетливых впечатлений от действия стимула. Это и определило характерные черты нового класса методов, детальная разработка которых осуществлена в последнее тридцатилетие — методов обнаружимости сигнала. Общим для всех методов этого класса является резкое обеднение стимульной ситуации (сведение ее всего до двух стимулов) и варьирование в качестве независимой переменной факторов, управляющих выбором ответа испытуемого. Описанию этих методов посвящена глава 2 данного раздела.

§1. Метод минимальных изменений

 

Данный метод является единственным среди методов измерения чувствительности, который дает знание величины порога в ходе самого измерения. В процедуре этого метода прямо отразилось понимание порога как барьера, разделяющего стимульный ряд на два класса ощущаемых и неощущаемых стимулов или их разностей.

1. Измерение абсолютного порога (RL) методом минимальных изменений.

Процедура. Существует несколько вариантов процедуры измерения этим методом. Рассмотрим процедуру Вундта. Каждая проба начинается сигналом " Внимание", после которого с постоянным интервалом (0, 5 - 1, 5 секунды) предъявляется стимул, например, пятно света при определении абсолютной световой чувствительности в полной темноте. Как правило, испытуемому разрешается только две категории ответов (" Да", " Нет"; " Вижу", " Не вижу" и т. п. ), форма которых точно оговаривается в инструкции испытуемому. Испытуемый отвечает, его ответ регистрируется. Предъявление стимулов осуществляется нисходящими и восходящими рядами. В первом случае степень выраженности определенного параметра стимула, чувствительность к которому измеряется, постепенно уменьшается от максимума до минимума, во втором — наоборот. Обычно измерение абсолютного порога начинается с нисходящего ряда стимулов, т. е. с отчетливо воспринимаемого стимула, изменяемый параметр которого с каждым шагом последовательно уменьшается. За порог в этом ряду принимается значение стимула, находящегося в середине межстимульного интервала между тем стимулом, который еще воспринимается, и тем, который впервые не воспринимается, т. е. середина того интервала, в котором произошла первая смена категории ответа испытуемого. В нисходящем ряду определяется порог исчезновения ощущения — L₁, в восходящем — порог появления — L_h (L — от латинского limen — порог). Чаще всего они не совпадают вследствие существования систематической ошибки.

Систематические ошибки бывают двух типов. Это так называемая ошибка привыкания, когда испытуемый продолжает повторять тот же ответ, что и на предыдущем шаге, хотя порог уже пройден и стимул в нисходящем ряду уже не вызывает ощущения, и ошибка ожидания или предвосхищения — ошибка противоположного толка. Для того, чтобы сбалансировать любую из этих ошибок, если они появляются, применяется: 1) уравновешивание числа тех и других рядов путем их чередования — нисходящие и восходящие ряды предъявляются парами, 2) требование от испытуемого ответа на каждый шаг изменения стимула в ряду. Для контроля за тщательностью работы испытуемого используется еще один экспериментальный прием — изменение длины стимульных рядов от пары к паре за счет смещения в случайном порядке начального и конечного значения стимулов в ряду. Эта предосторожность служит для предупреждения возможности повторения испытуемым своих ответных реакций на основе простого отсчета от начала и конца ряда определенного количества шагов изменения стимула*.

* Действительно, ведь сообразив в первых 2—3 рядах, что пороговая величина стимула соответствует где-то четвертому шагу изменения стимула в восходящем ряду из 10 шагов, испытуемый может в остальной части опыта заниматься только счетом: четвертый шаг снизу — " порог", шестой сверху — тоже " порог", и т. д.

 

При выборе величины шага изменения стимула надо учитывать следующие моменты. При уменьшении величины шага падает дисперсия ответов (Геррак, 1970), а, следовательно, и порогов в восходящих и нисходящих рядах, что позволяет сократить число пар рядов, не изменяя заданной точности измерения порога. Однако, уменьшение величины шага приводит к увеличению количества шагов в каждом отдельном ряду, т. е. к удлинению ряда и, следовательно, опыта в целом. Оптимальный размер шага является результатом компромисса между стремлением к большой точности в оценке порога и нежеланием делать опыт очень длинным и утомительным.

Необходимое число измерений (пар рядов) определяется требуемой точностью измерения и степенью разброса получаемых в эксперименте данных. Его можно вычислить по формуле:

 

 

где n — число измерений; U_p — квантиль нормального распределения, соответствующий заданной доверительной вероятности в определении порога; σ — дисперсия пороговых значений; δ — требуемая точность в определении порога.

Поскольку до начала опытов дисперсия пороговых значений неизвестна, для определения требуемого числа измерений необходимо провести предварительные пробные измерения, чтобы " прикинуть" величину дисперсии.

Обработка результатов. За абсолютный порог принимается среднее арифметическое всех найденных в течении опыта порогов появления и исчезновения и рассчитывается как:

 

 

где RL — средний абсолютный порог (обозначение RL — аббревиатура от немецкого " Reiz Limen" ); L_i — значение единичного порога в каждом стимульном ряду, как в восходящем, так и в нисходящем; N — общее число рядов.

Вариативность работы испытуемого оценивается средним квадратическим (стандартным) отклонением σ _L:

 

 

Статистическая ошибка, которая допускается, при вычислении в опыте абсолютного порога, оценивается стандартной ошибкой среднего значения:

 

2. Измерение дифференциального порога (DL) методом минимальных изменений.

Процедура. В этом случае все особенности метода и процедура остаются почти теми же, что и при определении абсолютного порога. Единственное изменение процедуры состоит в том, что одновременно с переменным стимулом испытуемому предъявляется эталон или стандартный стимул — S_st, который задает тот уровень исходного раздражителя, относительно которого выясняется величина разностного порога. В силу того, что ощущения различия стимулов у испытуемого могут быть различны, естественно разрешить испытуемому давать три категории ответов, а именно " больше", " меньше", " равно". Ответ " не знаю", " сомневаюсь" обычно отождествляется с ответом " равно". За порог принимается значение стимула, соответствующее середине межстимульного интервала, где впервые произошла смена категории ответа: от " больше" к " равно" и от " равно" к " меньше" в нисходящем ряду, а в восходящем ряду от ответа " меньше" к ответу " равно" и от ответа " равно" к ответу " больше". Таким образом, при измерении разностного порога определяются четыре значения порога (по два в каждом ряду). Это верхний порог — L_h в восходящем и нисходящем рядах ( L_h↑ , и L_h↓ ) и нижний порог — L_| в восходящем и нисходящем рядах (L_|↑ , и L_|↓ ). Таким образом, в каждом ряду мы находим две пороговые точки: верхний и нижний разностные пороги. На рис. 1 они помечены точками в каждом ряду. Этот рисунок иллюстрирует правило установления пороговой точки в нисходящих и восходящих рядах ответов испытуемого.

 

 

Обработка данных. Сначала находим значения верхнего разностного порога путем усреднения всехверхних порогов в каком бы ряду они не стояли:

 

 

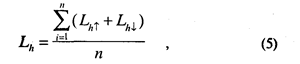
где L_h- и L_hï — значения верхних порогов в восходящем и нисходящем рядах, a n — число пар рядов.

Аналогичным образом вычисляем нижний разностный порог:

 

 

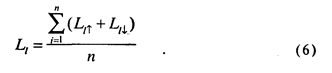
Верхний и нижний пороги ограничивают интервал неопределенности — IU (от английского " IntervalofUncertainty" ), т. е. ту зону стимульного ряда, где преобладают ответы равенства. Иначе говоря, интервал неопределенности — это та зона стимулов, которая сверху ограничена стимулом, в среднем едва заметно отличающимся от эталонного, как больший, а снизу — стимулом, в среднем едва заметно отличающимся от эталонного, как меньший. Понятно поэтому, что IU содержит две различительные ступени или два едва заметных различия, т. е. равен двум дифференциальным порогам DL (от немецкого " Differenz Limen" ):

 

 

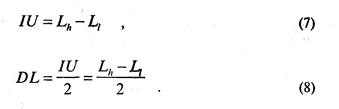
Стимул, находящийся в средней точке интервала неопределенности, всегда оценивается как равный эталону, т. е. является субъективным эквивалентом эталона и потому получил название точки субъективного равенства PSE (от английского " Point of Subject Equality" ):

 

 

IU, как правило, несимметричен, поэтому довольно часто PSE не совпадает со значением эталона. Степень несовпадения эталона PSE характеризуется так называемой константной ошибкой, СЕ (от английского " Constant Error" ), которая определяется следующим равенством:

 

 

Если константная ошибка больше нуля, то эталон переоценивается, если она меньше нуля, то эталон недооценивается. Таким образом, СЕ характеризует величину и направление смещения зоны субъективного равенства относительно объективного равенства. Соотношение этих основных психофизических понятий, которые используются и в других методах, иллюстрируется схемой, приведенной на рис. 2.

 

 

3. Варианты метода минимальных изменений.

Объединение пары рядов в один ряд. В этом случае восходящий и нисходящий ряды предъявляются без перерыва. Достоинство этого варианта в том, что он обеспечивает некоторое сокращение времени. Его существенным недостатком является увеличение при такой системе подачи стимулов нерегулярности ответов, обусловленной тем, что второй ряд в паре начинается со стимула, вызывающего слабое, неуверенное ощущение различия.

Процедура " вверх-вниз" (метод лестницы). Этот вариант метода границ, предложенный Корнсвитом (1962), предполагает использование двух вариантов ответов. Суть его состоит в том, что как только происходит смена категории ответа, допустим, смена ответа " слышу" на ответ " не слышу", так сразу же происходит смена направления изменения стимула, т. е. переход от нисходящего ряда к восходящему до следующей смены категории ответа. Этот вариант метода относится к так называемым адаптивным методам пороговых измерений, и, как правило, реализуется на компьютере, который отслеживает ответы испытуемого и соответствующим образом регулирует изменение стимуляции. В этих методах процедура тестирования строится таким образом, что предъявление стимулов подстраивается (" адаптируется" ) под ответы испытуемого, и изменение стимуляции происходит в достаточно узком околопороговом диапазоне (рис. 3).

 

 

Достоинством этой процедуры является экономичность, вместе с тем она имеет ряд недостатков. Один из них состоит в том, что эта модификация метода применима только к измерению абсолютного порога. Дифференциальный порог может измеряться этим методом только в разных двух сериях, а это плохо из-за временных колебаний чувствительности. Второй недостаток состоит в том, что испытуемый быстро замечает порядок чередования ощущаемых и неощущаемых стимулов, что вызывает эффект ожидания, распространяющийся по горизонтали, т. е. переносится с одного стимула на другой. Гилфорд (1954) отмечает, что этот эффект является таким сильным источником стабилизации результатов (несенсорным источником! ), равного которому нет ни в каком другом методе. Величину этой стабилизации трудно измерить и каким-либо образом скорректировать. Поэтому эта процедура применима только в случаях, когда исследователь может удовлетвориться очень грубым, но зато быстрым определением порога. На практике этот метод часто применяется для скрининговых исследований слуховой чувствительности.

Метод едва заметного различия (ЕЗР). Эту модификацию иногда полностью отождествляют с методом границ. Это не совсем точно. Суть метода ЕЗР сводится к следующему: испытуемому вместе с эталонным стимулом предъявляют ряд переменных. Задача испытуемого состоит в том, чтобы указать то значение стимула, которое едва заметно отличается от эталона. Существенное отличие метода ЕЗР от метода границ состоит в том, что в методе границ испытуемый определяет два порога — порог появления и исчезновения ощущения различия — ЕЗР и ЕНЗР, т. е. едва незаметного различия. В методе ЕЗР определяется только одна точка — всегда ЕЗР. Эти методы тождественны только тогда, когда изменение стимуляции начинается от равенства переменного и эталонного стимулов. В том случае, когда изменение стимуляции начинается от заметного неравенства к равенству, испытуемый определяет точку исчезновения ощущения различия (ЕНЗР), опираясь на сенсорный эталон, хранящийся в памяти.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: