Результаты эксперимента по определению пространственного порога тактильного восприятия

 

 

 

Чрезвычайно редко случается так, что одному из стимулов соответствует пороговая пропорция ответов: Р_{" два"} = 0, 5. Чаще всего соответствующую порогу точку приходится определять по полученной психометрической кривой. Графическим или вычислительным путем можно найти значения медианы (и среднего), характеризующих величину абсолютного порога (в нашем примере RL = 10, 57 мм) и меры вариативности — квартили Q₃, Q₁ и стандартного отклонения — σ.

Очевидно, что точность оценки порога обусловлена прежде всего " хорошестью" аппроксимации экспериментально полученных точек гладкой кривой. К сожалению, математически корректное решение задачи подгонки точки непросто. Поэтому на практике используются два варианта построения психометрической функции: 1) с помощью линейной интерполяции отдельных участков психометрической функции в линейных координатах; либо 2) вся психометрическая функция аппроксимируется функцией нормального распределения, которое в нормальных координатах является прямой линией. Рассмотрим оба эти случая обработки экспериментальных данных.

Обработка экспериментальных данных в методе констант

Способ линейной интерполяции. Этот способ не обеспечивает высокую точность, но зато крайне прост. Линейная интерполяция* основывается на представлении психометрической функции в виде отрезков прямой, которые проводятся между полученными точками. Этот случай представлен на рис. 11.

* Метод линейной интерполяции основан на допущении, что на участке между двумя экспериментальными точками психометрическая функция может быть приблизительно представлена в виде прямой. Такое предположение в известной степени правомерно, поскольку на интересующем нас участке между Q₁ и Q₃ психометрическая функция действительно похожа на прямую линию.

 

Простейшим и наиболее часто используемым является графический способ нахождения значений медианы и квартилей. Если на графике провести горизонтальные линии на уровне пропорций ответов, равных 0. 5, 0. 25, 0. 75, то их пересечения с построенной психометрической кривой дадут, сответственно, значения Md, Q₁ и Q₃, которые считываются с оси абсцисс в физических величинах стимула. Естественно, при использовании графического способа обработки результатов следует построить психометрическую функцию на координатной бумаге, выбрав достаточно крупный масштаб.

 

 

Те же значения могут быть получены и расчетным путем по следующим формулам (фактически эти формулы вытекают из решения прямоугольных треугольников):

Медиана психометрической кривой определяется как

 

 

где S_l — величина ближайшего к 50-процентной точке стимула, лежащего ниже ее, S_h — величина стимула, лежащего непосредственно выше 50-процентной точки, Р_l и Р_h — соответствующие указанным выше стимулам пропорции ответов.

Первый и третий квартили вычисляются по формулам:

 

 

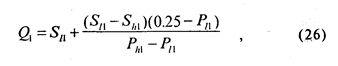
где S_l1 — величина стимула, лежащего непосредственно ниже 25-процентной точки,

S_h1 — величина стимула, лежащего непосредственно выше 25-процентной точки,

Р _l1 и Р_h1 — соответствующие указанным выше стимулам пропорции ответов.

 

 

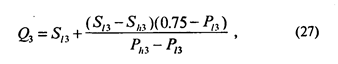
где S _l3 — величина стимула, лежащего непосредственно ниже 25-процентной точки; S_h3 — величина стимула, лежащего непосредственно выше 25-процентной точки; Р_l3 и Р_h3 — соответствующие указанным выше стимулам пропорции ответов.

В нашем примере Md = 10, 57 мм, Q₁ = 9, 83 мм, Q₃ = 11, 33 мм.

Недостатками способа линейной интерполяции являются:

1) расточительность, так как из всех полученных в эксперименте данных используется только часть — например, для определения Md достаточно иметь две точки;

2) отсутствие возможности получить точную оценку показателей разброса — дисперсии или межквартильного размаха — Q. Если в эксперименте используется больше двух стимулов, можно определить Q₁ и Q₃, а если допустить, что распределение частот ответов является нормальным, то можно найти и величину стандартного отклонения через соотношение σ = 1, 483Q. Однако при широком диапазоне используемых стимулов и относительно малом их числе (около 5, как в нашем примере) оценка Q будет не очень точной, следовательно, и значение σ также.

Способ нормальной интерполяции. Если сделать более строгое допущение о форме психометрической функции, а именно, что она является функцией нормального распределения, и если выразить масштаб оси ординат в единицах стандартного отклонения этого распределения, то психометрическая функция, имеющая S-образную форму в линейных координатах, превращается в прямую линию. После этого появляется возможность найти все интересующие исследователя параметры прямой, аналогично тому, как это делалось в случае линейной интерполяции. Но для этого нужно прежде всего преобразовать пропорции ответов Р с помощью таблиц нормального распределения в значения Z, представляющие собой нормированные по стандартному отклонению расстояния от стимульных точек до медианы. После преобразования Р в Z экспериментальные точки на графике, где по абсциссе отложен физический параметр стимула S, а по ординате — Z, могут быть аппроксимированы* прямой линией, которая проводится " на глазок" (этот способ хотя и прост, но чаще всего дает лишь грубое приближение), либо рассчитывается с помощью метода наименьших квадратов. Этот метод позволяет получить не только наилучшую аппроксимацию, но и статистически строго оценить степень " хорошести" подгонки полученной прямой к экспериментальным точкам.

* Термин " аппроксимация" экспериментальных точек какой-либо функцией означает процедуру представления (моделирования) набора эмпирических точек в виде определенной математической функции. В данном случае предполагается, что, если психометрическая функция — это функция нормального распределения, то в нормальных координатах она будет иметь вид линейной функции. Очевидно, что " хорошеть" арппок-симации экспериментальных точек линейной функцией будет одновременно служить показателем адекватности принятого предположения о нормальности распределения.

 

Определение медианы, представленной в z-координатах психометрической функции, возможно графическим и расчетным путем. За абсолютный порог (и PSE при измерении двухкатегориальным методом констант разностного порога) принимается величина стимула, которой соответствует Z = 0. Стандартное отклонение определяется как такая величина стимула, для которой Z = +1 или Z = -1*. Через стандартное отклонение можно найти и величину полумежквартильного размаха — Q, т. к. их связь в случае нормального распределения описывается равенством

 

* Фактически шкала z-оценок и является шкалой единиц стандартного нормального отклонения — σ. Точка z=0 соответствует нулевому отклонению от среднего (медианы), точки z = l или -1 — отклонению от среднего на 1σ вправо или влево, соответственно.

 

Для иллюстрации этого способа обработки обратимся к нашему примеру (см. табл. 2). Графическое представление зависимости величины Z_{" два"} от физического параметра стимула (т. е. психометрическая функция в нормальных координатах) приведено на рис. 11.

Определение с помощью графиков параметров психометрической функции способом нормальной интерполяции не требует преобразования в z-координаты, если имеется в наличии вероятностная бумага. Способ изготовления такой бумаги подробно описан (Бардин, 1976).

Все необходимые пороговые показатели могут быть определены и аналитическим путем с помощью соответствующих формул. Для этого можно воспользоваться двумя методами.

Во-первых, можно применить уже известный нам метод линейной интерполяции (теперь в нормальных координатах), который фактически является аналогом простого графического решения, когда мы не производим строгого построения аппроксимирующей прямой. Расчет параметров психометрической прямой производится по формулам (29), (30) и (31):

 

 

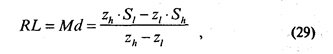
где z_l и z_h— самые близкие к нулю отрицательная и положительная величины z, соответственно; S_l и S_h — стимулы, соответствующие z_l и z_h (т. е. величины ближайшего подпорогового и надпорогового стимулов).

Для оценки величины стандартного отклонения следует взять разность между точками на стимульной оси, соответствующими z = l или z = -1 и величиной порога — RL. Эти точки можно вычислить так:

 

 

где z_l+. и z_h+ — ближайшие значения z, меньшие и большие +1, соответственно; S_h+ и S_l+ — стимулы, соответствующие z_l+ и z_h+ (т. е. ближайшие значения стимулов, ниже и выше S_{σ +}).

 

 

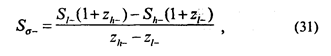
где z_l- и z_h- — ближайшие значения z, меньшие и большие -1, соответственно; S_h- и S_l- — стимулы, соответствующие z_l- и z_h- (т. е. ближайшие значения стимулов, ниже и выше S_{σ -}).

Оба значения S_{σ +} и S_{σ -} вычисляются в связи с тем, что полученная в эксперименте психометрическая кривая далеко не всегда является очень хорошим приближением к кривой нормального распределения, и эти значения могут расходиться. Поэтому обычно для оценки разброса используется их среднее. В нашем примере вычисления по приведенным формулам дали следующие величины:

 

RL = 10. 57 мм, S_{σ +} и S_{σ -} = 0. 98 мм.

 

Во-вторых, воспользовавшись методом наименьших квадратов, можно построить наилучшую прямую, проходящую через экспериментальные точки. Эта задача решается просто в любом статистическом пакете путем выполнения процедуры построения простой линейной регрессии. Вычислив таким образом коэффициенты а и b линейной функции у = ах+b, мы без труда найдем неизвестные " х" по известным " y" (z = 0, z = l или z = -l). Понятно, что поскольку точки S_{σ +} и S_{σ -} будут симметричны относительно RL, то достаточно вычислить лишь одну из них.

3. Варианты метода констант

Метод приращения. Особенностью экспериментальной процедуры является непрерывное предъявление испытуемому стандартного стимула, к которому периодически добавляются приращения. Испытуемый отвечает, заметил ли он приращение, в терминах, например, " Да" -" Нет". Разностным порогом является приращение стимула, заметное в 50% случаев. В методе приращений измеряется разностный порог реакции, представляющий собой половину интервала неопределенности. Сомнения в отношении возможности использования интервала неопределенности в качестве показателя различения уже высказывались выше.

В экспериментах, проводимых в поддержку нейроквантовой теории, практикуется вариант метода приращений, при котором в каждой экспериментальной серии используется лишь одна величина приращения. Наличие перерывов между экспериментальными сериями с разными величинами приращений является недостатком этого метода, поскольку допускает направленное изменение характеристик испытуемого в отношении приращений разной величины.

Метод АБХ. В этом методе испытуемому предъявляются последовательно три стимула: первый обозначается А, второй — Б, третий — X. Первые два стимула различаются величиной исследуемого параметра; в качестве третьего стимула (X) используется либо А, либо Б. Испытуемый должен ответить, какой из стимулов был X. Метод АБХ при условии запрещения нейтральных ответов сводится к двухкатегориальному варианту метода констант. Этот метод широко применяется в прикладных исследованиях, где обычно используются сложные стимулы, которые нетренированный испытуемый затрудняется классифицировать в терминах " больше" — " меньше", но хорошо понимает и может выполнить задачу идентификации, когда от него не требуется вынесения суждения только по одному из одновременно меняющихся сенсорных признаков при изменении физических параметров стимула. В качестве оценки чувствительности в этом методе используется полумежквартильный размах — 0(2). Однако эта оценка загрублена влиянием несенсорных факторов, приводящих к нестабильности критерия принятия испытуемым решения.

Для существенного уменьшения этого загрубления оценки Индлин (1979) предлагает ограничиваться в пределах одной непрерывной части опыта использованием одного сравниваемого стимула.

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: