§ 3. Построение пространственной модели стимулов

 

Как уже было сказано, построение психологического пространства предполагает решение двух самостоятельных задач: определения минимального числа осей, необходимых и достаточных для описания структуры межстимульных различий, и вычисления числовых значений, определяющих положение каждого стимула относительно базисных осей координат.

1. Определение базисной размерности.

Определение достаточного числа измерений основано на выборе некоторого критерия, по которому оценивается расхождение между исходной матрицей данных и вычисленными межточечными расстояниями. В идеальном случае это расхождение должно равняться нулю, но в эмпирических данных всегда присутствуют случайные ошибки — шум, величина которого чаще всего неизвестна, поэтому на практике критерий выбирается не нулевой, но достаточно небольшой.

Например, Торгерсон (1958) предлагает следующий метод для определения минимальной размерности. Вычисляется центрированная матрица скалярных произведений между стимулами. Характеристические корни этой матрицы упорядочиваются по величине. Размерность определяется по числу собственных векторов, соответствующих наибольшим характеристическим корням, так, чтобы разброс полученных координат вносил достаточно большой вклад в дисперсию (75—96%). Остальная часть дисперсии рассматривается как следствие случайных ошибок.

Метод определения минимального числа измерений в ходе построения пространственной модели впервые был предложен Шепардом (1962). Он основан на общем принципе понижения размерности, который представляет собой растяжение больших и сжатие маленьких расстояний. Действительно, чтобы поместить, например, треугольник в одномерном пространстве, не нарушая условия монотонности, необходимо сжать его меньшие стороны и растянуть большую. Процедура понижения размерности, так же как и достижение монотонности, основана на формировании множества векторов для каждой точки i, которые должны сжимать маленькие расстояния и растягивать большие. Критерием разделения расстояний на маленькие и большие служит среднее арифметическое расстояний. Поскольку процедура понижения размерности ориентирована на выполнение условия полной монотонности по отношению к различиям, то вместо рангов расстояний, которые на данном шаге итерации не обязательно удовлетворяют условию монотонности, лучше брать ранг самих различий. Тогда вектор, формирующийся для точки i по отношению к точке j, будет определять направление вектора (от точки i к точке j или наоборот), а величина разности (D_ij - D) будет определять длину вектора. Сформированные таким образом (n-1) векторы для данной точки i также рассматриваются как действующие аналогично (n-1)-мерному вектору. Как и в ходе достижения монотонности, на каждом шаге итерации меняется положение всех n точек.

При использовании подобных формальных критериев полезно учитывать, что качество аппроксимации исходных данных построенным пространством тем выше, чем больше выбранное число измерений (Спенс, 1972). При увеличении размерности величина ошибки монотонно убывает (рис. 1), поэтому предпочтительнее такое число осей r, при котором эта функция становится достаточно пологой.

 

 

Формальные критерии определения размерности имеют довольно приблизительную ценность, поскольку в каждом случае выбор критерия оказывается достаточно произвольным. Более важными являются другие критерии, которые основаны на хорошей содержательной интерпретации полученного решения. Содержательная интерпретация есть конечный результат производимого анализа, и в любом случае именно она определяет и значимость построенного пространства, и правильность выбора размерности.

Поэтому некоторые авторы (Крускал, 1964) предлагают производить отображения отдельно в одно-, двух-, трех- и т. д. -мерные пространства, строить там оптимальные конфигурации точек и затем выбрать из них такую, которая с точки зрения содержательной интерпретации даст наилучшее решение. Для хорошей интерпретации существенно правильное направление осей координат. В некоторых случаях (Виш и Кэррол, 1974) направление осей координат выбирается в ходе самого алгоритма построения пространственной модели, но в большинстве алгоритмов МШ оси координат имеют произвольное направление, поэтому для облегчения содержательной интерпретации используют вращение пространства с тем, чтобы получить оси, связанные с определенными группами стимулов. Аналогичным вспомогательным средством является и метод приведения к главным осям (Терехина, 1974).

Обычно только небольшое число осей получает удовлетворительную интерпретацию, остальные измерения чаще всего являются следствием экспериментального шума. Некоторые измерения могут быть связаны с отдельным подмножеством стимулов, или с данным типом испытуемых, поэтому большой разброс, полученный по данной размерности, еще не означает ее общей важности. Из этого следует очень важный вывод, что окончательное решение не может быть основано на результатах отдельных экспериментов, а необходимо исследование независимых групп данных с привлечением различных методов МШ.

2. Вычисление координат.

К настоящему времени для вычисления координат точек в психологическом пространстве различными авторами разработано большое количество разнообразных алгоритмов. В данной работе рассматриваются только три из них, которые непосредственно использовались для анализа экспериментальных данных.

Метод ортогональных проекций. Одним из наиболее простых метрических методов МШ является метод ортогональных проекций (Орлочи, 1967; Соколов и др., 1975). Суть его заключается в следующем.

Если есть множество точек, заданных расстояниями между ними, то мы можем максимальное из этих расстояний принять за первую ось (Х₁). Точки, заданные этим максимальным расстоянием, обозначим как 1 и 2, затем точку 1 на этой оси примем за начало оси Х₁ и спроектируем ортогонально все остальные точки на ось Х₁. Тогда точка 1 имеет координату Х₁₁ = 0, а точка 2 — координату X₁₂ = d₁₂.

Величина проекции для каждой точки i (кроме первых двух точек) вычисляется по известной геометрической формуле:

 

 

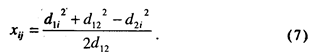
Далее легко вычисляются расстояния от каждой точки до оси X₁ по формуле:

 

 

Если все h_i = 0, то очевидно, что все точки лежат на оси X₁, т. е. пространство данных точек одномерно. Если некоторые h_i > 0, то из них выбирается максимальное (h_max) и принимается за ось Х₂, то есть h_max = X₂₃, а точка пересечения h_max с осью X₁ есть начало оси X₂ (рис. 2).

Затем все остальные точки ортогонально проецируются на ось Х₂ и величина проекции вычисляется по формулам:

 

 

Объединив эти формулы, получим:

 

 

Расстояние от каждой точки до плоскости Х₁Х₂ определится теперь как

 

 

 

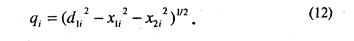
И в этом случае, если все q_i = 0, то, следовательно, все точки лежат на плоскости Х₁Х₂ и выделение следующей оси пространства не имеет смысла.

Далее, если q_i отличны он нуля, то выбирается точка с максимальным значением — q_max и принимается за четвертую точку, и тогда через эту точку 4 будет проходить ось Х₃. Далее вычисляются проекции всех остальных точек на эту ось:

 

 

Точка, наиболее удаленная от гиперплоскости в пространстве размерности r, ищется из условия:

 

 

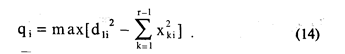
Процедура продолжается до тех пор, пока сумма всех проекций на k-ю ось не окажется меньше некоторого наперед заданного критерия. Например, эффективность решения можно определять отношением:

 

 

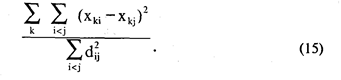
Обычно ограничиваются таким количеством осей, которое дает разброс, исчерпывающий до 70-90% дисперсии.

Число полученных осей рассматривается как минимальная размерность субъективного пространства, необходимая, чтобы удовлетворялась совместимость всех межточечных расстояний. Простота этого метода делает его удобным для применения к данным, структура которых имеет линейный характер. Однако получающаяся картина существенно зависит от первоначально взятых расстояний, т. е. решение оказывается зависимым от зашумленности исходных данных. Необходимо также отметить, что результирующее пространство определяется всего по нескольким точкам, и поэтому отдельные изолированные точки могут полностью определить решение задачи (Аустин, Орлочи, 1966). Очевидно, что метод, в котором пространство определяется разбросом всех точек, будет иметь более общий характер. Именно такой метод был предложен Торгерсоном (1952, 1958).

Метод Торгерсона. Метод метрического МШ, описанный в работах Торгерсона (1952, 1958), свободен от большинства недостатков метода ортогональных проекций и дает решение, независимое от начального этапа вычислений. Он основан на процедурах аппроксимации исходной матрицы матрицей меньшего ранга (Янг, Хаусхольдер, 1938).

Пусть d_ij, d_ik и d_jk — симметричные расстояния между тремя точками i, j и k. Рассмотрим симметричную матрицу В_i* с элементами b*_ij и размерностью (n-1)(n-1), где:

 

 

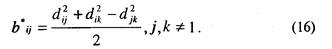
Элемент b*_ij представляет собой скалярное произведение векторов от точки i к точкам j и k. Это легко показать с помощью закона косинуса, где для любых трех точек

 

 

Из уравнений (16) и (18) следует, что b*_ij = d_ijd_ikcosφ, т. е. скалярному произведению векторов из точки i к точкам j и k. Любая из n точек может быть взята как точка i. Таким образом существуют n матриц В*, из которых каждая может быть взята как данная матрица скалярных произведений.

Теоремы Янга и Хаусхольдера показывают, как из матрицы скалярных произведений векторов, начинающихся в точке i, получить информацию о том, возможно ли разместить исходную совокупность точек в вещественном евклидовом пространстве, и если возможно, то какова его минимальная размерность и чему равны координаты точек на этих осях.

Теоремы Янга и Хаусхольдера относятся к любой В_i* матрице:

1. Если матрица В_i* положительно полуопределена, расстояния между стимулами могут рассматриваться как расстояния между точками, лежащими в действительном евклидовом пространстве. В терминах характеристических корней или собственных значений матрицы В_i* это означает, что точки могут рассматриваться лежащими в действительном евклидовом пространстве, если все корни или положительны, или равны 0. Отрицательные характеристические корни предполагают мнимые пространства.

2. Ранг любой положительной полуопределенной матрицы равняется размерности множества точек. Количество положительных значений равняется числу осей, необходимых для описания взаимных межточечных расстояний. Для данного набора стимулов матрица В_i* будет иметь один и тот же ранг, независимо от того, какой стимул выбран как начало.

3. Любая положительная полуопределенная матрица B_i* может быть факторизована для получения матрицы X, где:

 

 

Если ранг матрицы В_i* равен r, где r ≥  (n-1), тогда матрица X является прямоугольной матрицей (n-l) x r, элементы которой есть проекция точек на r-ортогональные оси с началом в i-ой точке r-мерного евклидова пространства. Допуская, что для выбора стимулов даны межточечные расстояния (не содержащие случайных ошибок), а матрица В_i* была построена в заданном начале, различные методики для факторизации матрицы В_i* дадут различные матрицы X, которые, однако, будут связаны ортогональным вращением осей. Матрицы В_i*, построенные посредством использования различных точек как начала расчета, дадут соответствующие матрицы X, которые не отличаются друг от друга с точностью до переноса и вращения осей.

Три теоремы, приведенные выше, определяют решение проблемы пространственной модели стимулов, когда заданы правильные межточечные расстояния. Первая теорема определяет, могут ли стимулы быть представлены точками действительного евклидова пространства. Вторая теорема дает критерии для определения минимальной размерности пространства. Третья теорема дает метод для получения проекций (шкальных оценок) на произвольном наборе осей пространства.

Однако на практике межточечные расстояния всегда даны нам с ошибками. Когда используются ошибочные оценки, то каждая точка будет отчасти ошибочной. Следовательно, в случае допущения, что истинная размерность значительно меньше, чем число стимулов, каждая матрица В_i* после факторизации даст результаты, которые более или менее различаются из-за ориентации осей и положения начала. При установлении начала в определенной точке возникает неявное предположение, что эта определенная точка является безошибочной. Таким образом мы сталкиваемся с проблемой выбора между n различными факторными матрицами, которые могут быть получены из данных. Одно из решений этой проблемы состоит в том, чтобы поместить начало координат не в какой-либо точке, а в центре тяжести всех точек-стимулов (Торгерсон, 1952, 1958, 1972). Эта процедура дает единственное решение и стремится взаимно компенсировать случайные ошибки для каждой отдельной точки. Опыт показывает, что помещение начала координат в центре тяжести всех точек приводит к меньшим ошибкам, чем помещение его в какую-либо произвольную точку. Рассмотрим процедуру для получения матрицы скалярных произведений векторов с началом в центре тяжести всех точек.

Пусть В_i* — матрица скалярных произведений размерностью (n-1)(n-1) с центром в точке i. Ее элемент:

 

 

Мы будем рассматривать В_i* как матрицу размерностью (n∙ n) с i-й строкой и j-ым столбцом, составленными из нулевых элементов. Таким же образом матрицу Х можно рассматривать как матрицу размерностью (n∙ r) с i-й строкой, составленной из нулевых элементов.

Наша задача — перенести оси координат из начала в точке i в начало, которое будет центром тяжести для всех точек.

Пусть Х⁰ — есть искомая матрица проекций точек j на ось е⁰ нескольких координатных систем с началом в центре тяжести n точек. Тогда:

 

 

и равно средней проекции точек на ось е (т. е. проекции центроида на ось e),

 

 

Подставляя уравнение (21) в уравнение (24), получим:

 

 

Из определения с_e видно, что

 

 

После подстановок получим:

 

 

Подстановка b_jk из уравнения (16) в уравнение (29) дает:

 

 

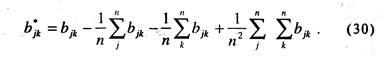
Суммирование каждого выражения в отдельности и упрощение приводитк:

 

 

Уравнение (31) дает стандартный прямой метод, чтобы из межточечных расстояний вычислить матрицу В* скалярных произведений с началом координат в центре тяжести всех точек. Получив оценки субъективных расстояний между всеми парами стимулов, уравнением (31) пользуются для вычисления матрицы В*. Затем эта матрица факторизуется посредством любого из. обычных методов факторизации для получения проекций стимулов на r ортогональных осей пространства, проходящих через центр тяжести всех объектов. Ориентация осей зависит как от конфигурации, так и от выбранного способа факторизации (Торгерсон, 1958). Матрица В* факторизуется в общем аналогично корреляционной или ковариационной матрице в методе главных компонент (Айвазян и др., 1974). По сравнению с другими ортогональными преобразованиями, преобразование к главным компонентам искажает структуру исходных данных наименьшим образом, поскольку всякий набор из данного числа главных компонент характеризует максимальный разброс точек, спроектированных в пространство этих главных компонент. Выбор числа главных компонент определяется величиной суммарной дисперсии, которую необходимо исчерпать в том или ином решении. На практике ограничиваются теми главными компонентами, которым соответствуют наибольшие характеристические корни, а все остальные компоненты отвергаются как незначительные.

Таким образом, метод Торгерсона дает возможность построить оптимальную пространственную модель стимулов в том смысле, что полученное решение не зависит от случайных экспериментальных ошибок, поскольку оно определяется структурой сразу всех стимулов. Однако необходимо учитывать, что пространственное представление стимулов, определенное по нескольким максимальным характеристическим корням матрицы скалярных произведений, может оказаться непригодным, если, например, истинная структура стимулов имеет локальные нелинейные цикличности (Терехина, 1977).

Алгоритм Янга-Торгерсона. Построение пространственной модели производится в два последовательных этапа. На первом этапе исходная матрица различий анализируется метрическим методом Торгерсона. По числу наибольших характеристических корней определяется размерность пространства, и таким образом формируется исходная конфигурация для n точек, между которыми вычисляются n(n-1)/2 расстояний.

На втором этапе данная конфигурация проверяется на выполнение условия монотонности. Для этого строится диаграмма монотонности. Она представляет собой график, осью абсцисс которого служат межточечные расстояния, а осью ординат — исходные различия. Каждой паре точек-стимулов (i, j) на этой диаграмме будет соответствовать точка с абсциссой d_ij и ординатой D_ij. Условие монотонности означает, что от начальной точки графика каждая последующая точка должна располагаться только правее или выше предыдущей, и никогда не может быть ниже или левее. Если, следуя этому правилу, соединить последовательно все точки отрезками, то получится график, характеризующий монотонность связи между межточечными расстояниями и исходными различиями. Очевидно, что если для каких-либо пар точек-стимулов (i, j) монотонность не выполняется, то точки, представляющие их на диаграмме монотонности, не попадут на построенный график, а будут левее или ниже его. Для каждой выпавшей из графика точки можно вычислить ее отклонение от графика по оси абсцисс расстояний (по оси ординат это отклонение измерять не нужно, поскольку порядок различий задан как исходный) и сумма этих отклонений

 

 

d_ij есть значение " правильной" абсциссы, для точки, выпавшей из графика монотонности) покажет степень несоответствия данной диаграммы условию полной монотонности.

Данный метод определения количественной меры достижения монотонности был предложен Крускалом (1964) и предложенная им мера была названа стрессом. Для достижения полной монотонности в алгоритме Янга—Торгерсона определяется матрица минимизирующая выражение (33). Количественной мерой достижения монотонности служит мера, названная авторами индексом адекватности:

 

 

В случае неудовлетворительного значения I найденные d_ij вводятся в исходную матрицу различий, и первый этап повторяется сначала. В обратном случае переходят к следующему этапу — улучшению исходной конфигурации. Для этого каждая координата Х точки i преобразуется с помощью выражения:

 

 

где р — коэффициент, определяющий сходимость итеративного процесса.

Новая конфигурация также проверяется на условие достижения монотонности по индексу адекватности I. Если I не получил удовлетворительного значения, то последний этап повторяется. В обратном случае решением являются координаты точек, полученные в последнем шаге итерации.

⇐ Предыдущая36373839404142434445Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: