Закон Кирхгофа

Для характеристики теплового излучения, мы будем пользоваться величиной потока энергии, измеряемой в ваттах.
Поток энергии, испускаемый единицей поверхности излучающего тела по всем направлениям (в пределах телесного угла 2π ), называют энергетической све­тимостью тела R
 Излучение состоит из волн различных частот ω (или длин λ ). Обозначим поток энергии, испускаемый едини­цей поверхности тела в интервале частот dω, черезdR_ω (чтобы не усложнять обозначений, мы опустили индекс «э» при R. При малой величине интервала dω поток dR_ω будет пропорционален dω.

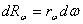(1)
Величина r называется испускательной спо­собностью тела. Опыт показывает, что испускательная способность сильно зависит от температуры тела. Таким образом, r есть функция частоты и температуры. Соответственно и энергетическая светимость является функцией температуры.
Зная испускательную способность, можно вычислить энергетическую светимость:

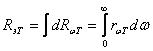(2)

(чтобы подчеркнуть, что энергетическая светимость и испускательная способность зависят от температуры, мы их снабдили индексом «T»).
Излучение можно характеризовать вместо частоты со длиной волны λ. Участку спектра dω будет соответство­вать интервал длин волн

Dλ . Определяющие один и тот же участок величины dω и dλ
связаны простым соотно­шением, вытекающим из формулы:

λ = c/v= 2π с/ω . Диф­ференцирование дает:

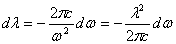(3)

Знак минус в этом выражении не имеет существенно­го значения, он лишь указывает на то, что с возраста­нием одной из величин, ω или λ, другая величина убы­вает. Поэтому знак минус в дальнейшем мы не будем писать.
Доля энергетической светимости, приходящаяся на интервал dλ, может быть по аналогии с (1) предста­влена в виде:

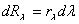(4)

Если интервалы dw и dl, входящие в выражения (1) и (4), связаны соотношением (3), т. е. отно­сятся к одному и тому же участку спектра, то величины dR_ω и dR_λ , должны совпадать:

.

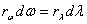Заменив в последнем равенстве dl согласно (3), получим:

,

откуда

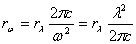
С помощью (5) можно перейти от r_λ к r_ω и на­оборот.
Пусть на элементарную площадку поверхности тела падает поток лучистой энергии dΦ _ω , обусловленный элек­тромагнитными волнами, частота которых заключена в интервале dω . Часть этого потока dΦ ′ будет поглощена телом. Безразмерная величина

(6)

называется поглощательной способностью тела. Поглощательная способность зависит от темпера­туры тела. Следовательно, а_{ω Т} есть функция частоты и температуры.

 

По определению а_{ω Т} не может быть больше единицы. Для тела, полностью поглощающего упавшее на него из­лучение всех частот, а_{ω Т} = 1. Такое тело называют абсолютно черным. Тело, для которого а_{ω Т} = а_Т = const < 1, назы­вается серым.
Между испускательной и поглоща­тельной способностью любого тела имеется определенная связь. В этом можно убедиться, рассмотрев следую­щий эксперимент. Пусть внутри за­мкнутой оболочки, поддерживаемой при постоянной температуре Т, поме­щены несколько тел (рис. 2). Полость внутри оболочки эвакуирована, так что тела могут обмениваться энергией между собой и с оболочкой лишь путем испускания и поглощения элек­тромагнитных волн. Опыт показывает, что такая система через некоторое время придет в состояние теплового рав­новесия — все тела примут одну и ту же температуру, равную температуре оболочки T. В таком состоянии тело, обладающее большей испускательной способностью r, теряет в единицу времени с единицы поверхности больше энергии, чем тело, обладающее меньшей r. Поскольку температура (а следовательно и энергия) тел не ме­няется, то тело; испускающее больше энергии, должно и больше поглощать, т. е. обладать большей а_{ω Т}. Таким образом, чем больше испускательная способность тела r_{ω Т}, тем больше и его поглощательная Способность а_{ω Т}. Отсюда вытекает соотношение:

,

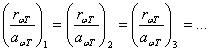где индексы 1, 2, 3 и т. д. относятся к разным телам.

Кирхгоф сформулировал следующий закон: отноше­ние испускательной и поглощательной способностей не зависит от природы тела, оно является для всех тел одной и той же, (универсальной) функцией частоты (длины волны) и температуры:

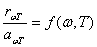(7)

Сами величины r_{ω Т}
и а_{ω Т}, взятые отдельно, могут ме­няться чрезвычайно сильно при переходе от одного тела к другому. Отношение же их оказывается одинаковым для всех тел. Это означает, что тело, сильнее поглощаю­щее какие-либо лучи, будет эти лучи сильнее и испускать (не следует смешивать испускание лучей с их отраже­нием).

Для абсолютно черного тела по определению а_{ω Т} = 1. Следовательно, нз формулы (7) вытекает, что r_{ω Т}
для такого тела равна f(ω, Т). Таким образом, универсальная функция Кирхгофа f(ω, Т) есть не что иное, как испускательная способность абсолютно черного тела.
При теоретических исследованиях для характеристики спектрального состава равновесного теплового излучения удобнее пользоваться функцией частоты —f(ω, Т). В экс­периментальных работах удобнее пользоваться функцией длины волны — φ (λ, Т). Обе функции связаны друг с другом формулой

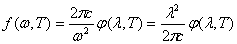, (8)

аналогичной формуле (5). Согласно (8) для того, чтобы по известной функции f(ω, Т) найти φ (λ, Т), нуж­но заменить в f(ω, Т) частоту ω через 2π с/λ и получив­шееся выражение умножить на 2π с/λ ²:

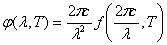(9)

Для нахождения f(ω, Т) по известной φ (λ, Т) нужно воспользоваться соотношением:

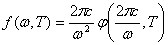(10)

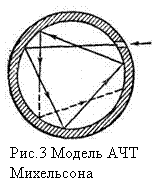
Абсолютно черных тел в природе не существует. Сажа или платиновая чернь имеют поглощательную способ­ность а_{ω Т}, близкую к единице, лишь в ограниченном интервале частот; в далекой инфракрасной области их поглощательная способность заметно меньше единицы. Однако можно создать устройство, сколь угодно близкое по своим свойствам к абсолютно черному телу.
Такое устройство представляет собой почти замкнутую полость, снабженную малым отверстием (рис. 3). Излучение, проникшее внутрь через отверстие, прежде чем выйти об­ратно из отверстия, претерпевает многократные отраже­ния. При каждом отражении часть энергии поглощается, в результате чего практически все из­лучение любой частоты поглощает­ся такой полостью. Согласно за­кону Кирхгофа испускательная спо­собность такого устройства очень близка к f(ω, Т), причем Т означает температуру стенок полости. Таким образом, если стенки полости под-церживать при некоторой температуре Т, то из отверстия выходит излучение, весьма близкое по спектрально­му составу к излучению абсолютно черного тела при той же температуре. Разлагая это излучение в спектр с помощью дифракционной решетки и измеряя болометром интенсивность различных участков спектра, можно найти экспериментально вид функции f(ω, Т) или φ (λ, Т). Результаты таких опытов приведены на рис. 4. Разные кривые относятся к различным значениям темпе­ратуры Т абсолютно черного тела. Площадь, охватывае­мая кривой, дает энергетическую светимость абсолютно черного тела при соответствующей температуре.

Кривые на рис. 4 очень похожи на кривые распре­деления молекул газа по скоростям. Правда, есть и существенное отличие. В то время как кривые распределения по скоростям для разных темпе­ратур пересекают друг друга (охватываемые ими площа­ди одинаковы), кривые спектрального распределения из­лучения абсолютно черного тела для более низких тем­ператур целиком лежат внутри кривых, соответствующих более высоким температурам (как мы увидим в следующем параграфе, площадь, охватываемая этими кривыми, пропорциональна четвертой степени температуры).
Из рис. 4 следует, что энергетическая светимость аб­солютно черного тела сильно возрастает с температурой. Максимум испускательной способности с увеличе­нием температуры сдвигается в сторону более коротких волн.
Закон Стефана — Больцмана и закон Вина

 

Теоретическое объяснение излучения абсолютно чер­ного тела имело огромное значение в истории физики — оно привело к понятию квантов энергии.
Долгое время многочисленные попытки получить тео­ретически вид функции f(ω, Т) не давали общего реше­ния задачи. Стефан (1879), анализируя эксперимен­тальные данные, пришел к выводу, что энергетическая светимость R_э любого тела пропорциональна четвертой степени абсолютной температуры. Однако последующие более точные измерения показали ошибочность его выво­дов. Больцман (1884), исходя из термодинамических со­ображений, получил теоретически для энергетической светимости абсолютно черного тела следующее значение:

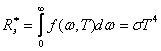(11)

где σ —постоянная величина, Т — абсолютная темпера­тура. Таким образом, заключение, к которому Стефан пришел для нечерных тел (с абсолютно черными телами он не экспериментировал), оказалось справедливым лишь для абсолютно черных тел.

Соотношение (11) между энергетической свети­мостью абсолютно черного тела и его абсолютной темпе­ратурой получило название закона Стефана — Больцмана. Константу σ называют постоянной Стефана — Больцмана. Ее экспериментальное зна­чение равно:

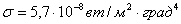(12)

Вин (1893), воспользовавшись, кроме термодинамики, электромагнитной теорией, показал, что функция спек­трального распределения должна иметь вид:

(13)

где F
— неизвестная функция отношения частоты к тем­пературе.

Согласно формуле (9) для функции φ (λ, Т) полу­чается выражение:

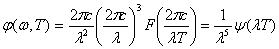(14)

где ψ (λ Т) — неизвестная функция произведения КТ.

Соотношение (4) позволяет установить зависимость между длиной волны λ _m, на которую приходится макси­мум функции φ (λ, Т), и температурой. Продифференци­руем (14) по λ:

(15)
Выражение в квадратных скобках представляет собой некоторую функцию ψ (λ T). При длине волны λ _т, соот­ветствующей максимуму функции φ (λ, T), выражение (15) должно обращаться в нуль:

.

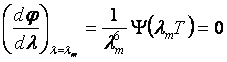Поскольку, как следует из опыта, λ _m≠ ∞, должно выполняться условие: Ψ (λ _тТ) = 0. Решение последнего уравнения относительно неизвестного λ _тТ дает для этого неизвестного некоторое число, которое мы обозначим буквой b. Таким образом, получается соотношение:

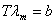(16)

которое носит название закона смещения Вина. Экспериментальное значение константы b
равно:

b=2, 90∙ 10⁷Å ∙ град=2, 90∙ 10³мк∙ град (17)

1. Тема 12: Квантовая физика

2. Курс: первый семестр: первый

3. Продолжительность лекции: 2 часа

4. Контингент слушателей: студенты

5. Учебная цель: изучение волновой оптики

6. Иллюстративный материал и оснащение: интерактивная доска

7. Подробный план:

1). Взаимодействие света с веществом.

2). Рассеяние света.

3). Поглощение света.

4). Закон Бугера-Ламберта-Бэра.

5). Оптическая плотность.

8. Методы контроля знаний и навыков: традиционные методы контроля.

9. Литература: см. в приложении.

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: