 |
Метод самосогласованного поля Хартри
|
|
|
|
Метод самосогласованного поля Хартри
Наиболее широко используемый и эффективный метод квантовой биологии.
Физическая идея метода заключается в следующем. Взаимодействие каждого электрона со всеми остальными заменяется взаимодействием с некоторым усредненным полем, создаваемым остальными электронами и ядрами.
Полная волновая функция представляется в виде произведения отдельных волновых функций электронов.
При этом предполагается, что все электроны независимы друр от друга
y=y1(1)y2(2)…yn(n)
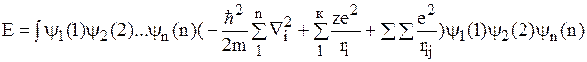
Метод Хартри-Фока дал возможность получить волновые функции большинства элементов периодической системы.
Для аналитической формы работы они не удобны, т. к. носят численный характер. При машинных работах этот недостаток устраняется. Были предприняты попытки и получены аналитические выражения, приблизительно описывающие эти численные результаты. Так же имеются приблизительные аналитические выражения, полученные как решения уравнения Шредингера различными приближенными методами.
Например, волновые функции для водородоподобных атомов могут быть представлены в виде: если
n=1 ℓ =0 m=0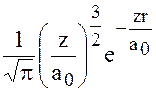 
n=2 ℓ =0 m=0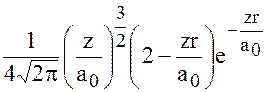 
n=2 ℓ =1 m=0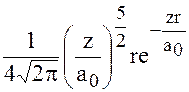 
a0-радиус первой орбиты Бора
Пусть имеется молекула с N ядрами и n электронами. тогда оператор энергии для данной молекулы должен содержать члены, описывающие кинетические энергии электронов и ядер, потенциальные энергии отталкивания электронов между собой, ядер между собой, энергию притяжения электронов и ядер.
Гамильтониан будет иметь следующий вид:
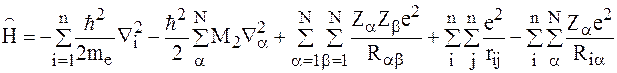
При строгом подходе волновая функция будет от электронных и ядерных координат y(r, R).
Основное осложнение вносит член Da-описывающий кинетическую энергию ядер. Из-за большой разницы в массах электронов и ядер, движение электронов происходит намного быстрее перемещения ядер, поэтому волновую функцию системы можно представить в виде
|
|
|
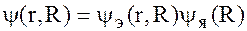, т. е.
считать, что движение электронов происходит независимо от движения ядер этой системы.
Поэтому электронную волновую функцию можно определить как собственную функцию оператора
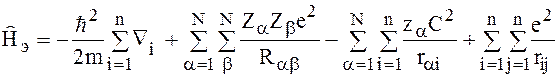
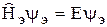
Метод молекулярных орбиталей
В методе молекулярных орбиталей (МО) полная волновая функция молекулы строится исходя из волновых функций, описывающих поведение отдельных электронов в поле, создаваемом остальными электронами и ядрами. Таким образом, метод МО отличается от метода атомных орбиталей тем, что МО являются многоцентровыми орбиталями. Поэтому основные идеи метода АО переносятся в метод МО. Подобно атомным орбиталям МО описывается одноэлектронной волновой функцией, т. е. зависит от координат только одного электрона.
Написанный оператор не зависит от спиновых переменных.
Чтобы учитывать наличие спина электронов волновая функция еще зависит от спиновых переменных и представляется в виде
j(rs)=j(r)Sz
Полная волновая функция описывается определителем
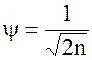
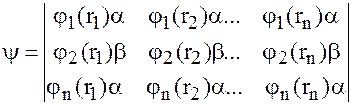
Полная энергия молекулы с этой волновой функцией определяется из обычного выражения
Ē =ò yĤ ydt
Приближение линейной комбинации атомных орбиталей.
Для получения МО можно применять метод Хартри-Фока, как и для атомов. Однако объем вычислений большой, и результат может быть получен за разумное время только для малых молекул. Хотя точность результатов является хорошей.
Для больших биологических молекул метод неприменим. Для больших молекул из приближенных методов наиболее распространенным является метод линейной комбинации атомных орбиталей (ЛКАО).
В этом методе МО аппроксимируется как линейная комбинация атомных орбиталей атомов, составляющего данную молекулу.
|
|
|
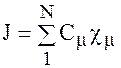, где
-заранее известная атомная орбиталь, Сm-произвольный постоянный коэффициент.
При таком представлении, если электрон находится вблизи ядра данного атома, то волновая функция для этого случая должна быть близка к атомной волновой функции данного тома, т. е. коэффициент перед этой орбиталью должен увеличиваться. Неизвестные коэффициенты находятся методом Ритца.
Среднее значение энергии определяется как
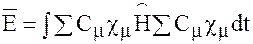
После минимизации по Сμ приходим к уравнениям
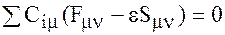m=1, 2…N, (6)
где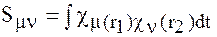 
интеграл перекрывания
Fmn- матричный элемент, сложная функция, зависящая Ĥ коэффициент Сim.
Поэтому система уравнений Рутана получается нелинейной. Она имеет нетривиальное решение если детерминант
.
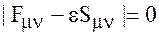Полученные величины ε из уравнения (а) подставляется в (в) и определяются сiμ . Эти итерации повторяются до тех пор, пока два последовательных значения энергии будут отличатся меньше, чем на ранее заданную величину. Объем вычислений огромен и под силу только ЭВМ.
Расчетное время возрастает при увеличении членов ряда разложения. Одновременно возрастает точность полученных результатов.
Квалификация исследователя проявляется в том, что он находит разумное сочетание точности и времени расчетов. Расчетное время возрастает пропорционально N4.
|
|
|
