Вариационный метод. Вариационный метод Ритца. Проблема одноэлектронных атомов

Вариационный метод

Точное решение уравнение Шредингера возможно только для простейших систем: атом водорода, молекулярный ион водорода. Большинство задач квантовой химии и биологии решается приближенными методами.

Среди значительного числа этих методов наиболее распространенными являются вариационный метод и теория возмущений.

Вариационный метод основывается на следующей теореме.

Если наименьшее собственное значение гамильтониана системы Ĥ равно Е₁ то ψ ₁ точная волновая функция этого состояния то для любой произвольной нормированной функция ψ выполняется соотношение

Ē =∫ ψ ^*Ĥ ψ dq≥ ∫ ψ ₁^*Ĥ ψ ₁dq=E₁ (6)

Произвольная функция ψ может быть представлена в виде ряда ортонормированных собственных функций любого эрмитового оператора, в том числе Ĥ .       

ψ =Σ С_iy_i    (7)

так как ψ нормирована

∫ ψ ^*ψ dt=Σ С_i^* С_jò y^* _iy_jdt=1 (8)

т. е. 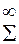С^*_iC_j =1 (9)

Подставим в (6) выражение (7)

Ē =SC^*_iC_jE_id_ji=SC²_iE_i (10)

SC²_iE₁ = Е₁ умножим выражение (9) Е₁ и полученное выражение вычтем из (10)

Ē - E₁=S С²_i(E_i- Е₁)

С²_i  всегда больше или равно 0 Е₁ наименьшее из возможных значений, следовательно, E_i- Е₁> 0 т. е. Ē - E₁≥ 0.

Из теоремы: собственное значение, соответствующее произвольной функции всегда больше или равно собственному значению точной волновой функции.

Функция y называется пробной волновой функцией. Чтобы пробная функция была ближе и точней волновой функции, и чтобы значения энергии, полученные с помощью этой волновой функции к истинному значению энергии пользуются варьируемыми параметрами С₁, С₂, С₃….

∂ Ē / ∂ С_i=0 из этого условия получаем оптимальные значения С_i.

Вариационный метод Ритца

В методе Рица пробная волновая функция y берется в виде линейной комбинации независимых функций

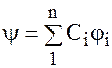, где С₁, С₂, С₃…. -варьируемые параметры

Подставив y в выражение Е=∫ ψ ^*Ĥ ψ dt, полагая y ненормированной

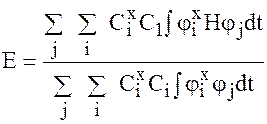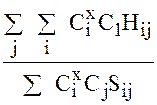= , где

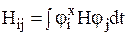- матричные элементы гамильтониана Н

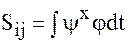-матричные элементы интегралов перекрывания

Уравнение можно представить в виде

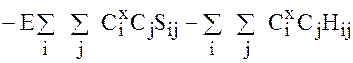
Условием минимума полученного выражения является 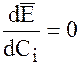, поэтому, проведя дифференцирование по C^x_i

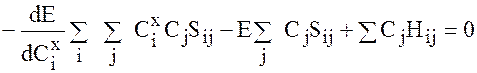
По условию 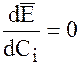, получается

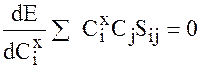
Оставшиеся члены выражения могут быть представлены в виде

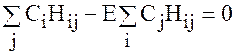
Вынося сумму за скобки, получаем выражение

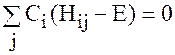(а)

Полученная система линейных однородных уравнений имеет нетривиальное решение только тогда, когда детерминант ее равняется нулю, т. е.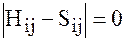

Это уравнение носит название секулярного уравнения. Решением являются значения энергии Е₁, Е₂, … Е_n

Наименьшая величина Е₁ соответствует энергии основного состояния. Остальные корни уравнения соответствуют возбужденным состояниям.

Определение волновых функций производится подстановкой полученной величины энергии в уравнение (а). Полученные постоянные величины С_i дают возможность определить волновую функцию.

Проблема одноэлектронных атомов

Оператор энергии для атома водорода имеет следующий вид

Решение уравнения находится в сферических координатах. Удастся разделить переменные. представляя y(r, q, j)=R_(r)q_(q)j_(j).

Волновая функция для водородоподобного атома имеет вид при значениях квантовых чисел n=1, ℓ =0, m=0

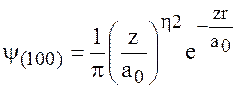
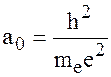
Оператор энергии для атома гелия включает новый член, описывающий взаимодействия электронов

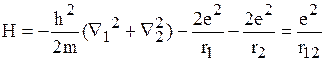
Ñ ₁²-оператор кинетической энергии электронов.

Ñ ₂²-оператор кинетической энергии ядер, 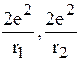-энергия взаимодействия электронов I и II с ядрами, последний член- энергия отталкивания электронов.

Наличие последнего члена создает сложности.

⇐ Предыдущая16171819202122232425Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: