Минимизация КНФ булевой функции

Если в СКНФ булевой функции произвести всевозможные операции обобщённого склеивания (xÚF)×(`xÚF)=(xÚF)×(`xÚF)×F, а затем операции поглощения F₁×(F₁ÚF₂)=F₁, то будет получена сокращённая КНФ, каждая элементарная дизъюнкция которой есть имплицента длины n или (n-1). На втором этапе выполняется операция обобщенного склеивания для имплицент длины (n-1), а в результате поглощения будут получены имплиценты длины (n-1) и/или (n-2).

Операции обобщённого склеивания и поглощения выполняются до тех пор, пока можно получать имплиценты от меньшего числа булевых переменных. Имплиценты минимальной длины булевой функции называются простыми.

Например, f(x₁;x₂;x₃;x₄)=(x₁Úx₂Úx₃Úx₄)×(x₁Ú`x<sub>2</sub>Úx<sub>3</sub>Úx<sub>4</sub>)×(x<sub>1</sub>Ú`x₂Ú`x<sub>3</sub>Úx<sub>4</sub>)×(x<sub>1</sub>Úx<sub>2</sub>Ú`x₃Úx₄)× (`x<sub>1</sub>Úx<sub>2</sub>Úx<sub>3</sub>Úx<sub>4</sub>)×(`x₁Úx₂Úx₃Ú`x<sub>4</sub>)×(`x₁Úx₂Ú`x<sub>3</sub>Ú`x₄).

· первый этап обобщённого склеивания:

f(x₁;x₂;x₃;x₄)=(x₁Úx₂Úx₃Úx₄)×(x₁Ú`x<sub>2</sub>Úx<sub>3</sub>Úx<sub>4</sub>)×(x<sub>1</sub>Ú`x₂Ú`x<sub>3</sub>Úx<sub>4</sub>)×(x<sub>1</sub>Úx<sub>2</sub>Ú `x₃Úx₄)× (`x<sub>1</sub>Úx<sub>2</sub>Úx<sub>3</sub>Úx<sub>4</sub>)×(`x₁Úx₂Úx₃Ú`x<sub>4</sub>)×(`x₁Úx₂Ú`x<sub>3</sub>Ú`x₄)×(x₂Úx₃Úx₄)× (x₁Úx₃Úx₄)×(x₁Úx₂Úx₄)× (x₁Ú`x<sub>2</sub>Úx<sub>4</sub>)×(x<sub>1</sub>Ú`x₃Úx₄)×(`x<sub>1</sub>Úx<sub>2</sub>Úx<sub>3</sub>)×(`x₁Úx₂Ú`x₄);

· первый этап поглощения:

f(x₁;x₂;x₃;x₄)=(x₂Úx₃Úx₄)×(x₁Úx₃Úx₄)×(x₁Úx₂Úx₄)×(x₁Ú`x<sub>2</sub>Úx<sub>4</sub>)×(x<sub>1</sub>Ú`x₃Ú x₄)× (`x<sub>1</sub>Úx<sub>2</sub>Úx<sub>3</sub>)×(`x₁Úx₂Ú`x₄);

· второй этап обобщённого склеивания:

f(x₁;x₂;x₃;x₄)=(x₂Úx₃Úx₄)×(x₁Úx₃Úx₄)×(x₁Úx₂Úx₄)×(x₁Ú`x<sub>2</sub>Úx<sub>4</sub>)×(x<sub>1</sub>Ú`x₃Ú x₄)× (`x<sub>1</sub>Úx<sub>2</sub>Úx<sub>3</sub>)×(`x₁Úx₂Ú`x₄)×(x₁Úx₄);

· второй этап поглощения:

f(x₁;x₂;x₃;x₄)=(x₂Úx₃Úx₄)×(`x<sub>1</sub>Úx<sub>2</sub>Úx<sub>3</sub>)×(`x₁Úx₂Ú`x₄)×(x₁Úx₄).

 

Следующий этап не уменьшает длину КНФ и числа двоичных переменных. Следовательно, получены простые имплиценты и тупиковая КНФ.

Для поиска минимальной КНФ составляется таблица простых имплицент, столбцами которой являются элементарные дизъюнкции СКНФ булевой функции - D⁽ⁱ⁾, а строками - простые имплиценты тупиковой КНФ - D_j.

Если D_j входят в число элементов D⁽ⁱ⁾, то на пересечении строки и столбца ставиться 1, в противном случае 0.

Для каждого значения D_j проверяется условие: если D_j⁽ⁱ⁾® Ú _l¹jD_l⁽ⁱ⁾º0, то D_j⁽ⁱ⁾ является ядерной имплицентой минимальной КНФ. Этому условию соответствует единственная 1 в столбце для соответствующего D_j.

Если в столбце несколько 1, то D_j⁽ⁱ⁾® Ú _l¹jD_l⁽ⁱ⁾º1. Удаляя из таблицы все ядерные имплиценты и столбцы D⁽ⁱ⁾, в которых они содержат 1, получим сокращённую таблицу неядерных имплицент КНФ, из числа которых следует выбрать набор простых имплицент с минимальным набором числа двоичных переменных.

Ядерные имплиценты и набор неядерных из числа простых имплицент КНФ, покрывающих все “1” таблицы, формирует минимальную КНФ. В таблице 1.28 представлены простые имплиценты тупиковой КНФ и элементарные дизъюнкции СКНФ для рассматриваемого примера.

таблица 1.28
Простые имплиценты Di	Элементарные дизъюнкты - Di
x1Úx2Úx3Úx4	x1Ú`x2Úx3Úx4	x1Ú`x2Ú`x3Úx4	x1Úx2Ú`x3Úx4	`x1Úx2Úx3Úx4	`x1Úx2Úx3Ú`x4	`x1Úx2Ú x3Ú`x4
x1Úx4		[1]	[1]	[1]
x2Úx3 Úx4
`x1Úx2Úx3					[1]
`x1Úx2Ú`x4Ú`x4

 

Элементами этой таблицы являются “1”, если простая имплицента входит в состав элементарной дизъюнкции СКНФ, и “0” – в противном случае. Квадратными скобками выделены те “1”, для которых выполняется условие ядерной имплиценты.

Ядерными имплицентами являются (x₁Úx₄) и (`x<sub>1</sub>Úx<sub>2</sub>Ú`x₄), которые покрывают элементарные дизъюнкции СКНФ (x₁Úx₂Úx₃Úx₄), (x₁Ú`x<sub>2</sub>Úx<sub>3</sub>Úx<sub>4</sub>), (x<sub>1</sub>Ú`x₂Ú`x<sub>3</sub>Úx<sub>4</sub>), (x<sub>1</sub>Úx<sub>2</sub>Ú`x₃Úx₄), (`x<sub>1</sub>Úx<sub>2</sub>Úx<sub>3</sub>Ú`x₄) и (`x<sub>1</sub>Úx<sub>2</sub>Ú`x₃Ú`x₄).

Из множества элементарных дизъюнкций D⁽ⁱ⁾ осталась непокрытой (`x₁Úx₂Úx₃Úx₄) и две неядерных имплиценты: (x₁×x₂×x₃) и (x₂×x₃×x₄). Следовательно, возможны два варианта минимальной КНФ:

. f^min(x₁;x₂;x₃;x₄)=(x₁Ú x₄)×(`x<sub>1</sub>Úx<sub>2</sub>Ú`x₄)× (x₂Úx₃Úx₄)

f^min(x₁;x₂;x₃;x₄)=(x₁Ú x₄)×(`x<sub>1</sub>Úx<sub>2</sub>Ú`x₄)× (`x₁Úx₂Úx₃).

Алгебра четких множеств

Если подмножества универсального множества U упорядочены отношением Í(X_i; X_j), то

а) операцию поиска верхней грани двух подмножеств называют объединением, т. е. SupX=(X_iÈX_j), где символ “È” есть оператор объединения,

b) операцию поиска нижней грани двух подмножеств называют пересечением, т. е. InfX=(X_iÇX_j), где символ ”Ç” есть оператор пересечения,

с) операцию поиска элементов универсального множества U, не принадлежащих множеству X_i, называют дополнением, т.е. ùX_i={x| xÏX_i и xÎU}, где символ “ù” есть оператор дополнения.

Множество всех подмножеств универсального множества - U вместе с двумя бинарными операциями и одной унарной представляют алгебру множеств, т. е.

A=< B (U), ù, È, Ç >,

где B (U) – носитель алгебры, а {ù; È; Ç} - сигнатура алгебры.

Операции над множествами

Для изображения исполнения отдельных операций обозначим прямоугольником универсальное множество U, а внутри него - кругами - подмножества A, B,... Заштрихованная область будет представлять результат исполнения операции. Такое изображение называют кругами Эйлера.

Объединение множеств А и В есть множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному множеству А или В, т.е.

С=(АÈВ)={x| xÎA или xÎB}.

Оператор объединения имеет вид:

С=union(A, B).

Если В=Æ, то АÈВ=АÈÆ=А. Если B=U, то АÈВ=АÈU=U.

Если АÍС и ВÍС, то

АÈВÍС.

Операцию объединения можно распространить на произвольное число подмножеств универсального множества U.

Например, если А₁, А₂,..А_nÍ U, то А₁ÈА₂È...ÈА_n=_i=1Èⁿ АⁱÍU.

 

Пример: даны множества A={a, b, c}, B={b, c, d, e}.

Найти C= (АÈВ). Ответ: C={a, b, c, d, e},

т.к. одинаковые элементы множеств записываются в формируемом множестве только один раз.

 

Пример: даны множества, которым принадлежат подмножества A={{a, b}, c}, B={{b, c, d}, c, d}. Найти C= (АÈВ).

Ответ: C={{a, b},{b, c, d}, c, d}, т.к. множества {a, b}ÎA, {b, c, d}ÎB.

Пример: даны множества несовместимых кортежей A={(a,b), (b, c)}, B={(b, c), (b, c, d), (c, d)}. Найти C= (АÈВ).

Ответ: C={(a, b), (b, c), (b, c, d,), (c, d)}.

Пример: даны отображения h¹ и h², представляющие множества совместимых кортежей. Найти h=(h¹Èh²).

Ответ: если все компоненты совместимых кортежей двух отображений имеют одинаковые значения, то формируется один кортеж (y, x₁, x₂,..x_n), при различии значений хотя бы одной компоненты формируются два кортежа (y⁽¹⁾, x₁⁽¹⁾, x₂⁽¹⁾,..x_n⁽¹⁾) и (y⁽²⁾, x₁⁽²⁾, x₂⁽²⁾,..x_n⁽²⁾).

В таблицах приведены результаты исполнения операции объединения.

h1

y

x1

x2

x3

È

h2

y

x1

x2

x3

=

h

y

x1

x2

x3

b

c

c

e

b

c

c

e

c

b

c

e

c

b

a

e

c

b

a

e

a

e

a

e

c

e

a

e

Пример: даны отношения r¹ и r₂. Найти r=(r¹Èr²).

Особенностью этой операции является исполнение дизъюнции для каждой позиции матриц смежности отношений r¹ и r², т. е.

r(x_i, x_j)=(r¹(x_i, x_j)Úr²(x_i, x_j)).

r1

x1

x2

x3

x4

r2

x1

x2

x3

x4

r

x1

x2

x3

x4

x1

x1

x1

x2

È

x2

=

x2

x3

x3

x3

x4

x4

x4

Пересечение множеств А и В есть множество, состоящее из всех элементов, которые принадлежат множеству А и множеству В: С=(АÇВ)={x|xÎA и xÎB}.

Операторная запись имеет вид: С=intersection(A, B).

 

Если В=Æ, то АÇÆ=Æ.

Если B=U, то АÇU=А.

Если СÍА и СÍВ, то СÍАÇВ.

Операцию пересечения можно раcпространить на произвольное число под- множеств универсального множества U.

Например, если А₁,...А_nÍ U,

то А₁ÇА₂Ç...Ç А_n=

_i=1Çⁿ АⁱÍU.

Пример: даны множества A={a, b, c} и B={b, c, d, e}.

Найти C= (АÇВ). Ответ: C={b, c}, т. к. b, cÎA и B.

Пример: даны множества A и B, которым принадлежат подмножества A={{a, b}, c}, B={{b, c, d}, c, d}. Найти C= (АÇВ).

Ответ: C={c}, т. к. {a, b}ÏB и {b, c, d}, dÏA.

Пример: даны множества несовместимых кортежей A={(a, b), (b, c)}, B={(b, c), (b, c, d), (c, d)}. Найти C= (АÇВ).

Ответ: C={(b, c)}, т. к. кортежи (a, b)ÏB, (b, c, d), (с, d)ÏA.

Пример: даны отображения h¹ и h². Найти h=(h¹Çh²).

Ответ: в таблицах приведены результаты исполнения операции пересечения двух отображений.

 

h1

y

x1

x2

x3

Ç

h2

y

x1

x2

x3

h

y

x1

x2

x3

b

c

c

e

=

c

b

c

e

c

b

a

e

c

b

a

e

a

e

a

e

Пример: даны отношения r¹ и r². Найти r=(r¹Çr²).

Особенностью этой операции является исполнение конъюнкции для каждой позиции матриц смежности отношений r¹ и r², т. е. r(x_i, x_j)=r¹(x_i, x_j)×r²(x_i, x_j).

В таблице приведены результаты исполнения операции пересечения.

r1

x1

x2

x3

x4

r2

x1

x2

x3

x4

r

x1

x2

x3

x4

x1

x1

x1

x2

Ç

x2

=

x2

x3

x3

x3

x4

x4

x4

 

Дополнение множества А есть множество, состоящее из всех тех элементов, которые принадлежат универсальному множеству U и не принадлежат множеству А, т.е.

ùА={x| xÎU и xÏA} 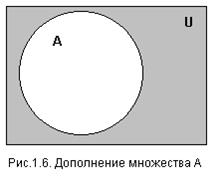Операторная запись дополнения имеет вид: ùА=complement(A).

Если существует ùА, то

АÇùА=Æ,

АÈùА=U и

ù(ùА)=А..

Пример: дано множество A={a, b, c} и универсальное множество U={a, b, c, d, e, f}. Найти C=ùА.. Ответ: C={d, e, f}.

Пример: дано множество A={{a, b}, c} и универсальное множество U={a, b, {a, b}, c, {d, e}, f}. Найти C=ùА.

Ответ:C={a, b, {d, e}, f}.

Пример: дано отображение h. Найти `h.

h
Y	a1	a2	a3	a1
X1	c2	c1	c1	c2
X2	d3	d1	d2	d1

Для поиска ùh необходимо найти множество кортежей, совместимых с кортежами h, но отличающихся значением хотя бы одной компонентой. Для этого определяют число элементов n области определения отображения (домен h) и число компонент кортежа k.

Тогда |ùh|= n ×(n -1)×(n -2)×..×(n - k +1) -|h|.

Если значения компонент кортежей не выходят за пределы своего атрибута, т. е. |Y|=3, |X₁|=2, |X₂|=3, то |ùh |=3×2×3 – 4=14.

В таблице представлены результаты вычисления кортежей отображения ùh для этого случая.

ùh

Y

a1

a1

a1

a1

a2

a2

a2

a2

a2

a3

a3

a3

a3

a3

X1

c1

c1

c1

c2

c1

c1

c2

c2

c2

c1

c1

c2

c2

c2

X2

d1

d2

d3

d2

d2

d3

d1

d2

d3

d1

d3

d1

d2

d3

Примечание: таблица размещена горизонтально.

Пример: дано отношение r. Найти `r.

Согласно правилу:

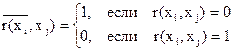
Ответ: в матрицах смежности r и `r приведены результаты исполнения этой операции.

r	x1	x2	x3	x4		`r	x1	x2	x3	x4
x1						x1
x2					Þ	x2
x3						x3
x4						x4

Операции дополнения, пересечения и объединения формируют две дополнительные операции: разности и симметрической разности.

Разность множеств А и В есть множество, состоящее из всех тех элементов, которые принадлежат множеству А и не принадлежат множеству В, т.е. С=(А\В)={x| xÎА и xÏВ},

где “\” - символ разности.

Оператор разности имеет вид: С=difference(A, B).

 

Очевидно, что С=(А\В)=(АÇ(ùВ)).

Пример: даны множества A={a, b, c} и B={b, c, d, e}.

Найти C= (А\В).

Ответ: C={a}, т.к. элементы b, сÎB.

Пример: даны множества A={{a, b}, c} и B={{b, c, d}, c, d}.

Найти C= (А\В).

Ответ: C={a, b}, т.к. элемент сÎB.

Пример: даны множества A={(a,b), (b, c)} и B={(b, c), (b, c, d),

(c, d)}. Найти C= (АÈВ).

Ответ: C={(a, b)}, т. к. кортеж (b, c)ÎB.

Пример: даны отображения h₁ и h₂. Найти h=(h₁\h₂).

Ответ: в таблицах приведены результаты исполнения этой операции.

h1

y

x1

x2

x3

\\

h2

y

x1

x2

x3

=

h

y

x1

x2

x3

b

c

c

e

b

c

c

e

c

b

c

e

c

b

a

e

a

e

a

e

Пример: даны отношения r₁ и r₂. Найти r=(r₁\r₂).

Ответ: особенность исполнения этой операции состоит в том, что
r(x_i, x_j)=(r₁(x_i, x_j)×`r<sub>2</sub>(x<sub>i</sub>, x<sub>j</sub>)). Следовательно, необходимо найти `r₂ и выполнить операцию пересечения r₁ и `r₂. В таблицах приведены результаты исполнения этой операции.

 

r1

x1

x2

x3

x4

r2

x1

x2

x3

x4

r

x1

x2

x3

x4

x1

x1

x1

x2

\

x2

=

x2

x3

x3

x3

x4

x4

x4

Симметрическая разность множеств А и В есть множество, состоящее из всех тех элементов, которые принадлежат разности (А\В) или (В\А), т. е.

С=(АDВ)=(АÇùВ)È(ВÇùА).

Оператор симметрической разности имеет вид:

С:=union(difference(A, B), difference(B, A)).

Если А=В, то (АDВ)=(АÇùВ)È(ВÇùА)=Æ.

Пример: даны множества A={a, b, c} и B={b, c, d, e}.

Найти C= (АDВ).

Ответ: C={a, d, e}, т.к. b, сÎA и b, сÎB.

Пример: даны множества A={{a, b}, c} и B={{b, c, d}, c, d}.

Найти C= (АDВ).

Ответ: C={{a, b}, {b, c, d}, d} т.к. сÎA и сÎB.

Пример: даны множества A={(a,b), (b, c)} и B={(b, c), (b, c, d),

(c, d)}. Найти C= (АDВ).

Ответ: C={(a, b), (b, c, d), (c, d)}, т. к. (b, c)ÎA и (b, c)ÎB.

Пример: даны отображения h₁ и h₂. Найти h=(h₁Dh₂).

Ответ: в таблицах приведены результаты этой операции.

 

h1

y

x1

x2

x3

D

h2

y

x1

x2

x3

=

h

y

x1

x2

x3

b

c

c

e

b

c

c

e

c

b

c

e

c

b

a

e

c

e

a

e

a

e

a

e

Пример: даны отношения r₁ и r₂. Найти r=(r₁Dr₂).

Ответ: особенность исполнения этой операции состоит в том, что

r(x_i, x_j)=(r₁(x_i, x_j) ×`r<sub>2</sub>(x<sub>i</sub>, x<sub>j</sub>)) Ú r<sub>2</sub>(x<sub>i</sub>, x<sub>j</sub>) ×`r₁(x_i, x_j).

В таблицах приведены результаты исполнения этой операции.

r1

x1

x2

x3

x4

r2

x1

x2

x3

x4

r

x1

x2

x3

x4

x1

x1

x1

x2

D

x2

=

x2

x3

x3

x3

x4

x4

x4

Законы алгебры множеств

Аксиомы общей алгебры формируют законы алгебрымножеств, если f_k=”Ú” и f_m=”×”:

· коммутативности: (AÈB)=(BÈA) и (AÇB)=(BÇA);

· ассоциативности: AÈ(BÈC)=(AÈB)ÈC; AÇ(BÇC)=(AÇB)ÇC;

· дистрибутивности: AÈ(BÇC)=(AÈB)Ç(AÈC); AÇ(BÈC)=(AÇB)È(AÇC);

· идемпотентности: AÇA=A и AÈA=A;

· поглощения: AÇ(AÈB)=A и AÈ(AÇB)=A;

· противоречия: AÇùA=Æ, AÈùA= U;

· двойного отрицания: ù(ùA)=A;

· закон де Моргана: ù(AÈB)= ùAÇùB и ù(AÇB)= ùAÈùB;

· свойства универсального и пустого множества:

AÈU=U и AÇU = A, АÈÆ=А и АÇU=A..

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: