 |
Глава 3. Основы теории графов
|
|
|
|
Теория графов находит самое широкое применение в моделировании информационных процессов, в проектировании вычислительных сетей, в программировании сложных вычислительных задач. Она представляет графическую интерпретацию сложных процессов. ”Картинка” позволяет быстро понять проблему и на интуитивном уровне разработать рациональный алгоритм решения.
Первая работа по теории графов была опубликована математиком Л. Эйлером в 1736г. в Трудах Академии наук Санкт-Петербурга в виде задачи о Кенигсбергских мостах.
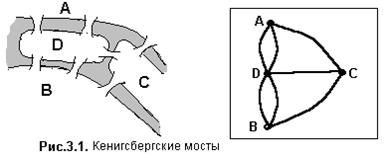
Суть задачи сводилась к следующему: мог ли житель Кенигсберга, выйдя из дома, находящегося на части суши (например, A, B, С или D), пройти по семи мостам города через реку Прегель в точности по одному разу и вернуться домой? Ответ на этот вопрос был отрицательным.
Для пояснения задачи представлена модель части города, прилегающей к реке Прегель (см. рис. 3.1), где каждый участок суши замещен точкой на плоскости, а мосты – линиями, связывающими участки суши.
Граф и его характеристики
Совокупность объектов произвольной природы и отношений между каждой парой этих объектов может быть изображена на плоскости в виде множества точек, являющихся образом множества объектов, и множества отрезков линий, соединяющих пары точек, что является образом множества отношений. Такой образ объектов и отношений принято называть графом. Множество точек, являющихся образом множества объектов, называют вершинами графа, а множество отрезков линий, являющихся образом множества отношений, - рёбрами или дугами графа.
Вершинами графа могут быть операторы программы и команды операционной системы, контактные площадки на плате компьютера и узлы компьютерной сети, события в любой сфере человеческой деятельности, а рёбрами – связи операторов программы, команд операционной системы, контактных площадок на плате компьютера, узлов в компьютерной сети, связи событий в любой сфере человеческой деятельности.
|
|
|
Граф может быть задан в двух формах:
а) G=<X, r>,
где r={ri=(xi, xj)| xi, xjÎX}Í(XÄX) есть отношения между вершинами графа,
б) G=<X; h>,
где h(xi)={xj| xjÎX} есть множество вершин графа, смежных вершине xi.
Первая форма применяется в тех случаях, когда необходимо отмечать дополнительные характеристики об отрезках линий, соединяющих вершины графа: протяжённость, загрузка, пропускная способность и т.п.
Вторая форма применяется в тех случаях, когда необходимо отмечать характеристики о вершинах графа: время исполнения команды или оператора, надёжность контактной площадки или загруженность узла компьютерной сети.
В зависимости от свойств, приписываемых различным компонентам и структурам графа, выделяют типы графов и формируют их характеристики.
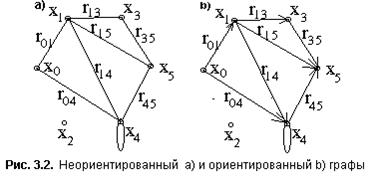
Граф называют неориентированным, если (xi, xj)=(xj, xi). Отрезок линии (xi; xj), соединяющий две вершины неориентированного графа, называют ребром.
Граф G=<X; r> называют ориентированным, если
(xi, xj)¹(xj, xi), а направленный отрезок линии (xi; xj), соединяющий две вершины, называют дугой.
На рис. 3.2. приведены неориентированный и ориентированный графы.
Любая программа или алгоритм вычислительного процесса, электронная схема или последовательность операций производственного процесса могут быть представлены ориентированным графом, а любая схема транспортной или электрической сети - неориентированным.Поскольку при описании графа используют элементы множеств вершин и отрезков линий, то для определения отношения принадлежности вершины графа отрезку линии и, наоборот, отрезка линии - вершине вводится понятие “инциденция”. Говорят, что вершина xi инцидентна ребру или дуге (xi, xj), если она является концевой вершиной данного отрезка линии, а ребро или дуга (xi, xj) инцидентна вершине xi, если отрезок линии ограничен концевой вершиной xi. Число вершин, инцидентных ребру или дуге, всегда равно 2, т.к. они являются концевыми вершинами отрезка линии, а число рёбер или дуг, инцидентных вершине xi, может быть произвольным. Число ребер, инцидентных вершине xi, называют степенью или валентностью вершины и обозначают
|
|
|
si=  .
.
Число дуг, исходящих из вершины xi, называют полустепенью вершины графа и обозначают si+=  .
.
Вершину xi, инцидентную исходящей дуге (xi, xj), называют истоком (символ ”+” отмечает вершину-исток).
Число дуг, заходящих в вершину xi, также называют полустепенью вершины графа и обозначают si-=  .
.
Вершину xi, инцидентную заходящей дуге (xj, xi)-, называют сто ком (символ ”-” отмечает вершину-сток).
Две вершины графа называются смежными, если они различны и между ними существует ребро или дуга.
Вершина xi, несмежная ни с одной вершиной графа, называется изолированной. На рис. 3.2. такой вершиной является x2 .
Два ребра называются смежными, если они различны и имеют общую вершину.
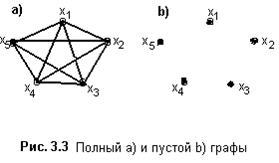
Граф называют полным, если любые две его вершины смежны между собой (см. рис. 3.3a) и пустым, если любые две его вершины не смежны (см. рис.3.3b).
Полный подграф некоторого графа называют кликой этого графа. В матрице смежности этого графа клика формирует единичный блок.
Граф называют дополнительным для графа G=<X; r>, если он опирается на множество вершин исходного графа и дополнение отношения r, т. е. ùG=<X;`r> (см. рис. 3.4).
Граф называют связным, если любые две его вершины можно соединить цепью. Для ориентированного графа выделяют сильную связность, когда любые две его вершины взаимодостижимы при наличии дуг, и слабую связность, когда любые две его вершины достижимы только при замене дуг на рёбра.

Граф называют деревом, если он связный, но без циклов, петель и кратных рёбер или дуг.
Ориентированные деревья интенсивно используют при орга- низации данных в компьютере, при синтаксическом анализе программ компиляторами, при формировании каталогов и орга- низации маршрутов.
В графе типа дерево (см. рис. 3.5) всегда  выделяют корневую вершину - J, узлы - прописные буквы латини- цы { A, B, C,..} и крону - строчные буквы латиницы { a, b, c,..}. Число дуг дерева всегда равно (n-1), где n - число вершин графа.
выделяют корневую вершину - J, узлы - прописные буквы латини- цы { A, B, C,..} и крону - строчные буквы латиницы { a, b, c,..}. Число дуг дерева всегда равно (n-1), где n - число вершин графа.
|
|
|
Вершинной связностью. графа G=<X; r> называют наи- меньшее число вершин, удаление которых приводит к несвязному графу. Например, если на рис. 3.5 удалить вершину J, то будет сформировано три дерева. Множество несвязных деревьев называют “лес”.
Реберной связностью графа G=<X; r> называют наимень- шее число ребер, удаление которых приводит к несвязному графу.
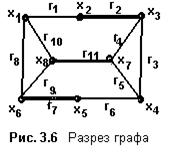
Если множество вершин графа G=<X; r> разбить на два подмножества X’ и X\X’ при условии, что X’È(X\X’)=X и X’Ç(X\X’)=Æ, то множество рёбер или дуг, одни из концевых вершин которых принадлежат множеству X’, а другие - множеству (X\X’), называют разрезом. Поиск разрезов сводится выделению множества рёбер, соединяющих эти подмножества.
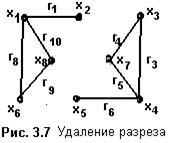
Пусть на рис. 3.6 дан граф G=<X; r>, где X={x1, x2,..x8}, а
r={r1, r2,..r11}. По условиям задачи выделено подмножество
X’={x1, x2, x6, x8}. Тогда X\X’={x3, x4, x5, x7}.
Разрезом является множество ребер {r2, r11, r7 }, которые выделены на рисунке полужирными линиями. Удаление разреза преобразует связный граф в несвязный. Так на рис. 3.7 изображены два связных подграфа графа, представленного на рис. 3.6, в результате удаления ребер разреза.
Последовательность смежных рёбер или дуг, соединяющих вершины xi и xj, называют маршрутом и обозначают m(i, j)=((xi, xk);…... (xl, xj)). Например, для неориентированного графа (см. рис. 3.2) между вершинами x0 и x5 существует шесть маршрутов, т.е. m05={(r04, r45); (r01, r14, r45); (r01, r1,5); (r04, r41, r15); (r04, r41, r13, r35); (r01, r13, r35)}.
Последовательность смежных вершин, соединяющая вершины xi и xj , называют переходом и обозначают n(i, j)=(xi,..xj). Например, для неориентированного графа (см. рис. 3.2) между вершинами x0 и x5 существует шесть переходов, т.е. n(0, 5)={(x0, x4, x5); (x0, x1, x4, x5); (x0, x1, x5); (x0, x4, x1, x5); (x0, x4, x1, x3, x5); (x0, x1, x3, x5)}.
Маршрут неориентированного графа, связывающий вершины xi и xj, называют цепью, а ориентированного - путём.
Маршрут называют открытым, если его концевые вершины различны, и замкнутым, если его концевые вершины совпадают.
|
|
|
Замкнутый маршрут неориентированного графа называют циклом, а ориентированного - контуром.
Маршрут называют простым, если при его обходе каждая промежуточная вершина встречается не более одного раза. Замкнутый простой маршрут неориентированного графа называют простым циклом, а ориентированного графа – простым контуром.
Замкнутый маршрут, который содержит только одно ребро или дугу, называют петлёй. На рис. 3.2 петля указана для x4. 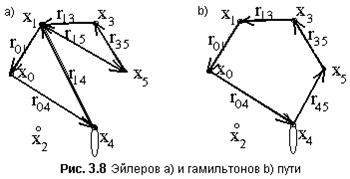
Маршрут называют эйлеровым, если он замкнут и проходит через каждое ребро графа только по одному разу. На рис. 3.8a) эйлеровым маршрутом является m(0, 0)=(r04, r14, r15, r35, r13, r01)}.
Граф G=<X; r> является эйлеровым тогда и только тогда, когда он связан и степень каждой вершины si есть четное число.
Маршрут называют гамильтоновым, если он замкнут и проходит через каждую вершину графа только по одному разу.
Таким на рис. 3.8b) является маршрут m(0, 0)=(r04, r45, r35, r13, r01)}.
Длина маршрута равна числу смежных рёбер, соединяющих вершины xi и xj , т.е. l(i, j)=Srk,l, где k¹l и i£k,l£j.
Длину минимального маршрута, соединяющего вершины xi и xj называют расстоянием. Например, расстояние между вершинами x0 и x5 графа на рис.3.8b) равно 2.
Если ребро или дуга обладают дополнительной характеристикой – протяжённостью – l(k, t), то длина маршрута равна сумме длин рёбер или дуг, его составляющих, т.е. l(i, j)=Sl(k, t), где k¹t и i£k,t£j.
Если ребро или дуга обладают дополнительной характеристикой - пропускной способностью – C(k, t), то пропускная способность маршрута равна минимальной пропускной способности ребра или дуги маршрута.
Существует несколько типов графов, сформированных на подмножествах вершин или ребер заданного графа.
Граф G’=<X’; r’> называют подграфом графа G=<X; r>, если он опирается на подмножество вершин исходного графа, т.е. X’ÍX, и инцидентных им рёбер.
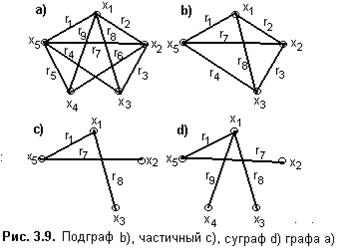
На рис. 3.9 приведен граф а) и его подграф b). Подграф задан подмножеством вершин X¢={x1, x2, x3, x5}ÍX вместе с инцидентными им ребрами r’= {r1, r2, r3, r4, r7, r8}Í.r.
Граф G’=<X’; r’> называют частичным для графа G=<X; r>, если он использует подмножество рёбер исходного графа, т.е. r’Ír, и инцидентные им вершины.
На рис. 3.9. приведен граф а) и частичный граф с). Частичный граф задан подмножеством рёбер r’={r1, r7, r8}Ír вместе инцидентными им вершинами X’={x1, x2, x3, x5}ÍX.
Граф G’=<X; r’> называют суграфом для графа G=<X; r>, если он использует подмножество рёбер исходного графа, т.е. r’Í r, и все вершины исходного графа.
На рис. 3.9. приведен граф а) и его суграф d). Суграф задан подмножеством рёбер графа r’={r1, r7, r8, r9}Ír и множеством вершин исходного графа X={x1, x2, x3, x4, x5}ÍX.
|
|
|
Суграф G’=<X’; r’>, формируемый без циклов, петель и кратных рёбер, называют остовом графа G=<X; r>.
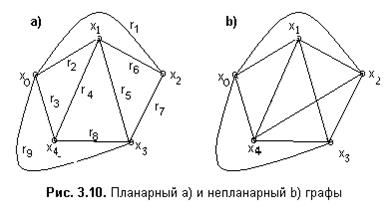
Граф называют плоским или планарным, если он может быть изображён на плоскости так, что рёбра или дуги графа не пересекаются. Плоские графы используют при проектировании печатных плат, сетей телекоммуникации и т.п.
На рис. 3.10 приведены для сравнения планарный и непланарный графы. У непланарного графа ребро (x1, x3) при любой трассировке будет пересекать ребро (x2, x4) или (x0, x2), а ребро (x2, x4) – пересекать ребро (x1, x3) или (x0, x3).
Граф G=<X;r> называют двудольным, если его множество вершин может быть разбито на два непересекающихся подмножества X’ и X\X’ так, что каждое ребро графа G соединяет две вершины из разных подмножеств. Граф является двудольным тогда и только тогда, когда все его циклы имеют четную длину.
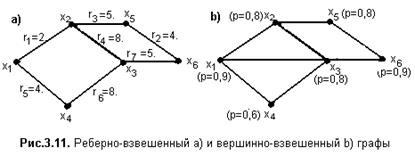
Граф G=<X;r> называют взвешенным, если его рёбра или вершины имеют дополнительные характеристики.
На рис. 3.11а). приведен реберно-взвешенный граф. Дополнительными характеристиками каждого ребра могут быть объем передаваемой информации или стоимость ее передачи, протяжённость или пропускная способность ребра. Каждому ребру графа приписана условная характеристика – вес.
На рис. 3.11b). приведен вершинно-взвешенный граф. Дополнительными характеристиками каждой вершины могут быть время исполнения команды или оператора программы, вероятность наступления события или надёжность эксплуатации узла и т.п. Каждой вершине графа приписана условная характеристика – вес.
Описание графа
Граф может быть задан списком или матричными структурами.
Списки. При описании графа списками используют модели G=<X; r> и G=<X; h>.
Первая форма - список отношений - применяется в тех случаях, когда необходимо хранить информацию о весе ребра (протяжённость, загрузка, пропускная способность линии связи и т.п.) и поиска инцидентных вершин.
В таблице 3.1 приведены характеристики графа, описанного рис.3.11а) по модели G=<X; r>.
| Таблица 3.1. | |||||||
| ri | r1 | r2 | r3 | r4 | r5 | r6 | r7 |
| (xi, xj) | (x1,x2) | (x5,x6) | (x2,x5) | (x2,x3) | (x1,x4) | (x3,x4) | (x3,x6) |
| l(ri) |
Вторая форма - список смежности - применяется в тех случаях, когда необходимо хранить информацию о весе вершины (время исполнения оператора, надёжность контактной площадки или загруженность узла и т.п.) и поиска смежных вершин.
В таблице 3.2.приведены характеристики графа, описанного рис.3.11b) по модели G=<X; h>.
| Таблица 3.2 | ||||||
| xi | x1 | x2 | x3 | x4 | x5 | x6 |
| h(xi) | x2, x3, x4 | x1, x3, x5 | x1, x4, x6 | x1, x3 | x2, x6 | x3, x5 |
| p(xi) | 0,9 | 0,8 | 0,8 | 0,6 | 0,8 | 0,9 |
При описании графа матрицами используют, прежде всего, матрицы инциденции и матрицы смежности
Матрица инциденции. Поскольку инциденцияесть отношение принадлежности элемента одного множества другому, то для графа G=<X, r> матрица инциденции ||q|| фиксирует эту принадлежность элемента множества r элементу множества X на множестве {0, 1}. Строки матрицы есть элементы множества r, а столбцы – элементы множества X. Элементы матрицы инциденции неориентированного графа определяются по формуле:
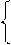 1, если ri=(xi, xj) инцидентно xj,
1, если ri=(xi, xj) инцидентно xj,
q(i. j) =
0, в противном случае.
В каждой строке матрицы количество единиц равно двум, а в каждом столбце - степени вершины - si .
В таблице 3.3. приведена матрица инциденции для неориентированного графа, представленного на рис. 3.2.
Особый интерес представляют петли на графе. Например, у вершины x4 есть петля, концевые вершины которой принадлежат x4. При задании графа с петлями рекомендуется расщеплять матрицу на две: матрицу-истоков и матрицу-стоков, т. е рассматривать две матрицы ориентированного графа.
| Таблица 3.3. | ||||||
| q | x0 | x1 | x2 | x3 | x4 | x5 |
| r01 | ||||||
| r04 | ||||||
| r13 | ||||||
| r14 | ||||||
| r15 | ||||||
| r35 | ||||||
| r44 | 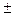 1 1
| |||||
| r45 | ||||||
| s |
Элементы матрицы инциденции для ориентированного графа определяют по другой формуле:
 +1, если ri,j исходит из вершины xi;
+1, если ri,j исходит из вершины xi;
q(i. j)= 0, если ri,j не инцидентна вершинам xi и xj;
-1, если дуга ri,j заходит в вершину xj.
В таблице 3.4 приведена матрица инциденции для ориентированного графа, представленного на рис. 3.2.
| Таблица 3.4. | ||||||
| q | x0 | x1 | x2 | x3 | x4 | x5 |
| r01 | +1 | -1 | ||||
| r04 | +1 | -1 | ||||
| r13 | +1 | -1 | ||||
| r14 | +1 | -1 | ||||
| r15 | +1 | -1 | ||||
| r35 | +1 | -1 | ||||
| r44 | ||||||
| r45 | +1 | -1 | ||||
| s+ | ||||||
| s- |
В каждой строке сумма “+1” и “-1” равна нулю, т. к. “+1” представляет вершину – исток, а “-1” вершину – сток.
При задании ориентированного графа с петлями рекомендуется расщеплять вершину с петлей на две вершины: вершину-исток и вершину-сток,
В каждом столбце матрицы число “+1” равно полустепени исхода вершины xi, т.е. si +, а число “-1” равно полустепени захода вершины xi , т.е. si -.
М атрица смежности. Поскольку смежность есть отношение между элементами одного множества, то матрица смежности ||ri,j|| есть квадратная матрица, число строк и столбцов которой равно мощности множества |X|=n.
Элементы матрицы смежности определяются соотношением
 1, если xi смежна xj;
1, если xi смежна xj;
r(i, j) =
0, в противном случае.
В таблице 3.5 представлена матрица смежности для неориентированного графа (см. рис. 3.2а).
Петля у вершины x4 формирует “1” на диагонали матрицы (xi, xj). В таблице можно выделить дополнительную строку или столбец для хранения информации о степени каждой вершины графа.
.
| Таблица 3.5 | |||||||
| r | x0 | x1 | x2 | x3 | x4 | x5 | si |
| x0 | |||||||
| x1 | |||||||
| x2 | |||||||
| x3 | |||||||
| x4 | |||||||
| x5 | |||||||
| si |
В таблице 3.6 представлена матрица смежности для ориентированного графа (см. рис. 3.2b), но при условии, что строки заданы вершинами-истоками, а столбцы - вершинами-стоками.
.
| Таблица 3.6 | |||||||
| r | x0 | x1 | x2 | x3 | x4 | x5 | si+ |
| x0 | |||||||
| x1 | |||||||
| x2 | |||||||
| x3 | |||||||
| x4 | |||||||
| x5 | |||||||
| si- |
Поэтому итоговый столбец таблицы - si+ показывает полустепени вершин-истоков, а итоговая строка - sI- - полустепени вершин-стоков.
По матрицам смежности можно сделать следующие выводы:
· каждый ненулевой элемент главной диагонали соответствует петле на графе;
· матрица смежности для неориентированного графа симметрична относительно главной диагонали;
· матрица смежности для ориентированного графа несимметрична относительно главной диагонали;
· столбец ориентированного графа, все элементы которого имеют значение “0”, соответствует вершине-истоку всего графа (см. таблицу 3.6);
· строка ориентированного графа, все элементы которой имеют значение “0”, соответствует вершине-стоку всего графа (см. таблицу 3.6).
Матрица весов. Матрица весов вершинно-взвешенного графа есть матрица-столбец, число строк которой равно числу вершин n, а позициями – значение веса вершины:
 .
.
Матрица весов реберно-взвешенного графа есть квадратная матрица, число строк и столбцов которой равно числу вершин графа. Позиции матрицы весов (xi, xj) при i¹j определяются соотношением:
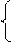 0, если i=j;
0, если i=j;
L(i, j) = li,j, если вершина xi смежна вершине xj и вес ребра li,j;
¥, если вершина xi несмежна вершине xj.
В таблице 3.7 дана матрица весов для графа на рис. 3.11а).
| Таблица 3.7 | |||||||
| L | x1 | x2 | x3 | x4 | x5 | x6 | |
| x1 | µ | µ | µ | ||||
| x2 | µ | µ | |||||
| x3 | µ | µ | |||||
| x4 | µ | µ | µ | ||||
| x5 | µ | µ | µ | ||||
| x6 | µ | µ | µ |
Матрица достижимости. Поскольку h(xi) есть множество вершин, которые смежны вершине xi, или “окрестность” вершины xi, или достижимы из xi за “один шаг”, то отображение h(h(xi))=h2(xi) есть вершины графа, достижимые из xi за “два шага” через вершины, сформированные на “первом шаге”. Отображение h(h(h(xi)))=h3(xi) есть вершины, достижимые из вершины xi за ”три шага” через вершины, сформированные на втором шаге. Так как любая вершина связного графа должна быть достижима за p£n “шагов”, то множество вершин достижимых из вершины xi за это число “шагов” может быть представлено в виде:
qp(xi)=IÈh(xi)È h2(xi) È..Èhp(xi),
где I –диагональ матрицы.
Для построения матрицы достижимости удобно использовать матрицу смежности, т.е.
||qp||=IÈ||r||È||r2||È||r3||È..È||rp.
Для возведения в степень матрицы смежности используют правило умножения булевых матриц:
ri,j2=k=1 Ú n (ri,k × rk,j),
ri,j3=k=1 Ú n (ri,k × rk,j2) и так далее.
Пример: в таблице r дана матрица смежности неориентированного графа. Определить достижимость каждой вершины графа.
Окрестностью вершины x1 является {x2, x4}, x2 – {x1, x3}, x3 – {x2, x4}, x4 – {x1, x3}.
| r | x1 | x2 | x3 | x4 | q | x1 | x2 | x3 | x4 | |
| x1 | x1 | |||||||||
| x2 | x2 | |||||||||
| x3 | x3 | |||||||||
| x4 | x4 | |||||||||
| r2 | x1 | x2 | x3 | x4 | q2 | x1 | x2 | x3 | x4 | |
| 1 | x1 | |||||||||
| x2 | x2 | |||||||||
| x3 | x3 | |||||||||
| x4 | x4 |
Ответ: любая вершина графа достижима не более, чем за “два шага”.
Пример: дана матрица смежности ориентированного графа. Определить достижимость каждой вершины графа.
| r | x1 | x2 | x3 | x4 | q | x1 | x2 | x3 | x4 | |
| x1 | x1 | |||||||||
| x2 | x2 | |||||||||
| x3 | x3 | |||||||||
| x4 | x4 |
| r2 | x1 | x2 | x3 | x4 | q2 | x1 | x2 | x3 | x4 | |
| 1 | x1 | |||||||||
| x2 | x2 | |||||||||
| x3 | x3 | |||||||||
| x4 | x4 |
| r3 | x1 | x2 | x3 | x4 | q3 | x1 | x2 | x3 | x4 | |
| x1 | x1 | |||||||||
| x2 | x2 | |||||||||
| x3 | x3 | |||||||||
| x4 | x4 |
Ответ: любая вершина графа достижима не более, чем за “три шага”.
Матрица разрезов. Если можно построить множество разрезов в виде совместимых кортежей, то можно оформить матрицу разрезов b, строками которой являются индексированные разрезы bi, а столбцами – ребра графа rj, одни из концевых вершин которых принадлежат множеству X’, а другие - множеству (X\X’),. Элементы матрицы разрезов вычисляют по формуле:
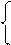 1, если j-е ребро участвует в i-м разрезе,
1, если j-е ребро участвует в i-м разрезе,
b(i, j)=
0, в противном случае.
Например, если x1ÎX’, а x4ÎX\X’ (см. рис. 3.6), то можно оформить не менее 18 разрезов, разъединяющих эти вершины. Ниже в таблице 3.8 приведена матрица только для пяти разрезов.
| Таблица 3.8 | |||||||||||
| b | r1 | r2 | r3 | r4 | r5 | r6 | r7 | r8 | r9 | r10 | r11 |
| b1 | |||||||||||
| b2 | |||||||||||
| b3 | |||||||||||
| b4 | |||||||||||
| b5 |
Матрица циклов. Если в графе существует несколько циклов, т их описание удобно сосредоточить в матрице циклов с, каждая строка которой есть индексированный цикл ci, а каждый столбец – ребро, включаемое в цикл.
Элементы матрицы циклов вычисляют по формуле:
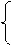 1, если j-е ребро участвует в i-м разрезе,
1, если j-е ребро участвует в i-м разрезе,
c(i, j)=
0, в противном случае.
Для графа, приведенного на рис. 3.10а) можно оформить не менее 18 циклов. Ниже в таблице 3.9 приведена матрица только для шести циклов этого графа.
Таблица 3.9
| с | r1 | r2 | r3 | r4 | r5 | r6 | r7 | r8 | r9 |
| c1 | |||||||||
| c2 | |||||||||
| c3 | |||||||||
| c4 | |||||||||
| c5 | |||||||||
| с6 |
Числа графа
Функции, заданные на множестве графов {G=<X; r>} и принимающие значения на множестве целых чисел, называют числовыми характеристиками или просто числами. Наиболее очевидными и простыми числами являются: число вершин - n, число рёбер - m, степени вершин - si(или si+/si-). Остальные числа графа требуют вычисления их значений.
Число компонент связности графа G=<X; r>. Граф называют связным, если любая пара его вершин связана цепью или путем.
Если множество вершин графа разбить на попарно непересекающиеся, непустые подмножества X={X1’, X2’,...Xk’}, т. е Xi’ÇXj’=Æ для i¹j и Xi¹Æ, то формируемые с помощью инцидентных X’i ребер r’iÍr подграфы G1=<X1’;r1’>, G2=<X2’;r2’>,…, Gk=<Xk’;rk’> являются связными, а между собой – несвязными, т. е. GiÇGj=Æ. Связный подграф Gi называют компонентой связности, а их количество - числом компонент связности k(G).
Для поиска числа компонент связности k(G) используют механизм вычисления матриц достижимости (см. 3.3).
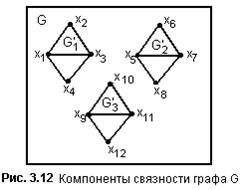
На рис. 3.12. представлен граф и его три компоненты:
G=<X; r>, где X={x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11},
G1=<X1; r1>, где X1={x1, x2, x3, x4}, G2=<X2; r2>, где X2={x5, x6, x7, x8}, G3=<X3; r3>, где X3={x9, x10, x11}.
Цикломатическое число графа G=<X; r>. Для исследования циклов в графе используют цикломатическую матрицу С(G), столбцы которой есть ребра графа, а строки c(I, j)– возможные циклы.
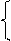 1, если j-е ребро входит в i-й цикл,
1, если j-е ребро входит в i-й цикл,
с(i, j) =
0, в противном случае.
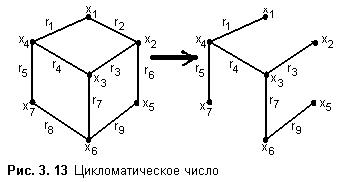
Например, для графа, приведенного на рис. 3.13, ниже представлена цикломатическая матрица, описывающая все циклы. Таких циклов - семь.
Наименьшее число рёбер, удаление которых приводит к графу без циклов и петель, называют цикломатическим числом и обозначают l(G). Цикломатическое число можно определить по формуле l(G)=m-n+k(G), где m - число рёбер, n - число вершин, k(G) - число компонент связности графа. Для графа G, приведенного на рис. 3.13, имеем n=7, m=9, k(G)=1. Следовательно, l(G)=9-7+1=3.
Связный граф, не содержащий ни одного цикла, называют деревом.
Ниже приведена матрица для семи циклов графа, приведенного на рис. 3.13.
| С(G) | r1 | r2 | r3 | r4 | r5 | r6 | r7 | r8 | r9 |
| c1 | |||||||||
| c2 | |||||||||
| c3 | |||||||||
| c4 | |||||||||
| c5 |
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|

