 |
Поиск неизвестного множества
|
|
|
|
Если одно из множеств тождества A=B содержит подмножество X, т. е. A(X) и/или B(X), то для нахождения X следует воспользоваться условием: если A=B, то (ADB)=(АÇùВ)È(ВÇùА)=Æ, и выделить алгебраические выражения известных подмножеств, элементы которых принадлежат также множествам X и ùX. Для того, чтобы (АÇùВ)È(ВÇùА)=Æ необходимо и достаточно приравнять пустому множеству алгебраические выражения известных подмножеств, элементы которых принадлежат также множествам X и ùX.
Если алгебраическое выражение известных подмножеств, элементы которого принадлежат также множеству X обозначить (...)1, т. е. ((...)1ÇХ)=Æ, то XÍù(...)1.
Если алгебраическое выражение известных подмножеств, элементы которого принадлежат также множеству ùX обозначить (...)2, т. е. ((...)2ÇùX)=Æ, то (...)2ÍX.
Алгоритм поиска:
шаг 1: если A=B, то записать выражение (АÇùВ)È(ВÇùА)=Æ;
шаг 2: в (АÇùВ)È(ВÇùА) найти алгебраические выражения известных подмножеств (...)1 и (...)2, элементы которых принадлежат также множеству X, т. е. ((...)1ÇХ), или его дополнению ùX, т. е. ((...)2ÇùХ);
шаг 3: если в (АÇùВ)È(ВÇùА) окажется алгебраическое выражение – (...)3, свободное от X или ùX, то найти его пересечение с универсальным множеством, т.е. (...)3Ç(XÈùX), и преобразовать по закону дистрибутивности в выражение ((...)3ÇX)È((...)3ÇùX);
шаг 4: если (АÇùВ)È(ВÇùА)=Æ, то
((...)1È(...)3)ÇХ=Æ,
((...)2È(...)3)ÇùХ=Æ;
шаг 5: если ((...)1È(...)3)ÇХ=Æ, то XÍù((...)1È(...)3) и
если ((...)2È(...)3)ÇùХ=Æ, то ((...)2È(...)3)ÍX.
Следовательно, ((...)2È(...)3)ÍXÍù((...)1È(...)3).
|
|
|
Дополнительными условиями можно уточнить значение X.
Пример: найти множество X по условиям (ХÈМ)=N и M и N –известные множества.
· ((XÈM)ÇùN)È(NÇù(XÈM))=Æ;
· ((XÈM)ÇùN)È(NÇùXÇùM)=Æ;
· (XÇùN)È(MÇùN)È(NÇùXÇùM)=Æ;
· (XÇùN)È(MÇùN)Ç(XÈùX)È(NÇùXÇùM)=Æ;
· XÇùN)È(XÇ(MÇùN))ÈùXÇ(MÇùN)È(ùXÇ(NÇùM))=Æ;
· (XÇ(ùNÈ(MÇùN))ÈùXÇ(MÇùNÈNÇùM)=Æ;
· (XÇùN)È(ùXÇ(MDN)=Æ;
Откуда XÇùN =Æ и ùXÇ(MDN) =Æ;
Следовательно, (MDN)ÍXÍN.
Если (ХÈМ)=N, то (ХÈМ)ÍN и NÍ(XÈM), т. е. МÇ(ùN)=Æ.
Тогда (МDN)=(N\ùM) и (N\M)ÍXÍN.
Следовательно, X=(N\M).
Пример: найти множество X по условию:
A\X=B,
AÈX=C при условии A, B, С – известные множества и BÍAÍC.
· 
AÇùX=B,
AÈX=C;
· 
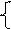(AÇùX)ÇùBÈù(AÇùX)ÇB=Æ,
(AÈX)ÇùCÈù(AÈX)ÇC=Æ;
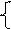· (AÇùBÇùXÈ(ùAÈX)ÇB=Æ,
AÇùCÈùCÇXÈùAÇCÇùX=Æ;
· 
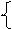(AÇùX)ÇùBÈù(AÇùX)ÇB=Æ,
(AÈX)ÇùCÈù(AÈX)ÇC=Æ;
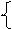· AÇùBÇùXÈùAÇBÇ(XÈùX)ÈBÇX=Æ,
AÇùCÇXÈAÇùCÇùXÈùCÇXÈùAÇCÇùX=Æ;
· 
AÇùBÇùXÈùAÇBÇXÈùAÇBÇùXÈBÇX=Æ,
AÇùCÇXÈAÇùCÇùXÈùCÇXÈùAÇCÇùX=Æ;
· AÇBÇXÈBÇX ÈAÇùBÇùXÈùAÇBÇùX =Æ,
AÇùCÇX ÈùCÇXÈAÇùCÇùXÈùAÇCÇùX=Æ;
· 
(ùAÇBÈB)ÇX È(AÇùBÈùAÇB)ÇùX =Æ,
(AÇùCÈùC)ÇXÈ(AÇùCÈùAÇC)ÇùX=Æ;
· BÇX È(ADB)ÇùX =Æ,
|
|
|
ùCÇXÈ(ADC)ÇùX=Æ;
· если BÍAÍC, то (ADB)=(A\B) и (ADC)=(A\C).
Следовательно,
BÇX È(A\B)ÇùX =Æ,
ùCÇXÈ(A\C)ÇùX=Æ.
(A\B)ÍXÍùB;
(С\A)ÍXÍC.
По условию BÍAÍC.
Тогда X = (C \ B).
Алгебра нечетких множеств
Если уиверсальное множества U содержит нечеткие помножества, то к этим подмножествам также применимы бинарные операции объединения X'=(X’iÈX’j) и пересечения X’=(X’iÇX’j) и унарная операция дополнения ùX’=U\X'. Особенностью исполнения таких операций над нечеткими множествами является поиск степени принадлежности для каждого элемента универсального множества.
Множество нечетких подмножеств универсального множества B ’(U) вместе с двумя бинарными операциями и одной унарной формируют алгебру нечетких множеств:
A’=< B ’(U), ù, È, Ç, mx’(u)>,
где B ’(U) – множество всех нечетких подмножеств универсального множества,
ù, È, Ç, - сигнатура алгебры,
mx’(u) – функция принадлежности элемента универсального множества U нечеткому подмножеству X’.
|
|
|
