Аксиомы и правила введения и удаления логических связок

Как уже отмечалось, множество формул поля интерпретации может быть очень большим. Среди формул этого поля можно выделить подмножество тождественно истинных формул. На этом подмножестве можно строить различные системы аксиом, достаточные для вывода новых формул.

Известна система из трех аксиом, использующая две логических связки “®” и “ù” или система из пяти аксиом, использующая логические связки “®” и “Ú”.

Однако наибольшей популярностью пользуется счистема из двенадцити аксиом, использующая логические связки “ù”, ”&”, “Ú” и ”®”. Эта система позволяет наиболее удобно и за меньшее число шагов организовать вывод заключения.

 

А1. F₁®(F₂®F₁);

А2. (F₁® F₂)® ((F₂® F₃))® (F₁® F₃));

А3. (F₁& F₂)®F₁;

А4. (F₁& F₂)®F₂;

А5. F₁®(F₂®(F₁&F₂));

А6. F₁®(F₁ÚF₂);

А7. F₂®(F₁ÚF₂);

А8. (F₁®F₃)®((F₂®F₃)®((F₁ÚF₂)®F₃));

А9. (F₁®F₂)®((F₁®ù F₂)®ù F₁);

A10. (F₁®F₂)®((F₁&F₃)®(F₂&F₃));

A1 1. (F₁® F₂)®((F₁ÚF₃)®(F₂ÚF₃));

А12. ùù F₁ ® F₁.

 

Для проверки истинности аксиом достаточно рассмотреть таблицы истинности для A2 и A8.

 

А2. (F₁® F₂)®((F₁®(F₂® F₃))®(F₁® F₃)).

F1	F2	F3	1®2	1®3	2®3	1®6	7®5	4®8
л	л	л	и	и	и	и	и	и
л	л	и	и	и	и	и	и	и
л	и	л	и	и	л	и	и	и
л	и	и	и	и	и	и	и	и
и	л	л	л	л	и	и	л	и
и	л	и	л	и	и	и	и	и
и	и	л	и	л	л	л	и	и
и	и	и	и	и	и	и	и	и

 

А8. (F₁® F₃)®((F₂ ® F₃)®((F₁ Ú F₂)® F₃))

 

F1	F2	F3	1Ú 2	1®3	2®3	4®3	6®7	5®8
л	л	л	л	и	и	и	и	и
л	л	и	л	и	и	и	и	и
л	и	л	и	и	л	л	и	и
л	и	и	и	и	и	и	и	и
и	л	л	и	л	и	л	л	и
и	л	и	и	и	и	и	и	и
и	и	л	и	л	л	л	и	и
и	и	и	и	и	и	и	и	и

 

Для понимания правил формирования аксиом следует рассмотреть правила введения и удаления логических связок. Это облегчит формирование промежуточных результатов и заключения.

 

 

П1. Если F₁ и F₂ имеют значение “и”, то истинной является их конъюнкция, т.е.

F₁; F₂ (F₁&F₂).

Эта запись тождественна аксиоме А5.

П2. Если (F₁&F₂) имеет значение “и”, то истинными являются формулы F₁ и F₂, т.е.

(F₁&F₂) (F₁&F₂)

F₁ и F₂.

Эта запись тождественна аксиомам А3 и А4.

П3. Если истинна хотя бы одна посылка F₁ или F₂, то истинной является их дизъюнкция, т.е.

F₁ F₂

(F₁ÚF₂) или (F₁ÚF₂).

Эта запись тождественна аксиомам А6 и А7.

П4. Если F₂ имеет значение “и”, то истинной является (F₁®F₂) при любом значении F₁, т.е.

F₂

(F₁®F₂).

Эта запись тождественна аксиоме А1.

П5. Если формула (F₁®F₂) имеет значение “и”, то истинной является формула (ùF₂®ùF₁), т.е.

(F₁®F₂)

(ùF₂®ùF₁).

Эта запись тождественна аксиоме А9 и называется законом контрапозиции.

 

П6. Если формула (F₁®F₂) имеет значение “и”, то истинной является формула ((F₁ÚF₃)®(F₂ÚF₃) при любом значении F₃, т.е (F₁®F₂) ((F₁ÚF₃)®(F₂ÚF₃)).

Эта запись тождественна аксиоме А11.

П7. Если формула (F₁®F₂) имеет значение “и”, то истинной является формула ((F₁&F₃)®(F₂&F₃)) при любом значении F₃, т. е.

(F₁®F₂)

((F₁&F₃)®(F₂&F₃)).

Эта запись тождественна аксиоме А10.

П8. Если формулы (F₁®F₂) и (F₂®F₃) имеют значение “и”, то истинной является формула (F₁®F₃), т.е

(F₁®F₂); (F₂®F₃)

(F₁®F₃).

Эта запись тождественна аксиоме А2 и называется законом силлогизм;

П9. Если формулы (F₁®F₂) и (F₂®F₁) имеют значение “и”, то истинной является формула (F₁«F₂), т.е.

(F₁®F₂); (F₂®F₁)

(F₁«F₂).

П10. Если формула (F₁«F₂) имеет значение “и”, то истинными являются формулы (F₁®F₂) и (F₂®F₁), т.е.

 

(F₁«F₂) (F₁«F₂)

(F₁®F₂) и (F₂®F₁).

Метод дедуктивного вывода

Выводом формулы В из множества формул F₁; F₂;... F_n называется такая последовательность формул, что любая F_i есть либо аксиома, либо выводима из множества предшествующих ей формул F₁; F₂;... F_n.

В этом случае формулу B называют заключением, а последовательность формул F₁; F₂;... F_n, сформированная отношением следования, представляет схему дедуктивного вывода.

Схему дедуктивного вывода записывают так:

 

F₁; F₂;... F_n |¾ B,

где символ “|¾ “ означает “верно, что B выводима из F₁;... F_n“.

Известна другая форма записи схемы:

 

F₁; F₂;... F_n

B,

где над чертой записывают множество посылок и аксиом F₁; F₂;...F_n, а под чертой - заключение В.

На языке математики схема дедуктивного вывода есть доказательство теоремы:

|¾ F₁&F₂&... &F_n®B.

Используя правила эквивалентных преобразований формулы теоремы, можно показать дедуктивный характер вывода заключения:

1) |¾(F₁&F₂&...&F_n®B);

2) |¾(ù(F₁&F₂&...&F_n )ÚB);

3) |¾(ùF₁ÚùF₂ Ú...ÚùF_nÚB);

4) |¾(ùF₁ÚùF₂ Ú...ÚùF_n-1Ú(F_n®B));

.....................................................

n) |¾(F₁®(F₂ ®...®(F_n-1®(F_n®B))...).

 

Таким образом, вывод заключения всегда логически следует из множества посылок и аксиом. Кроме того, вывод заключения опирается на два основных правила:

а) если F_i и (F_i ® F_j) выводимые формулы, то F_j также выводимая формула:

F_i; (F_i®F_j)

F_j.

Это правило называют modus ponens (m.p.) или способ прямого доказательства.

b) если ùF_j и (F_i®F_j) выводимые формулы, то ùF_i также выводимая формула:

ù(F_i®F_j)

ùF_i.

Это правило называют modus tollens (m.t.) или способ обратного доказательства.

Пример: суждение: “Сумма внутренних углов многоугольника равна 180^о (А). Если сумма внутренних углов многоугольника равна 180^о (A), то многоугольник есть треугольник (В). Следовательно, дан треугольник (В)”.

Формула этого суждения (m.p.) имеет вид:

А; A®B

B.

Пример: суждение: ”Дан не треугольник (ùB). Если сумма внутренних углов многоугольника равна 180^о (А), то многоугольник есть треугольник (В). Следовательно, сумма внутренних углов многоугольника не равна 180^о(ùA)”.

Формула этого суждения (m.t.) имеет вид:

ùB; A®B

ùA.

Пример. доказать истинность заключения:

(A Ú B); (A®C); (B®D)

(CÚD).

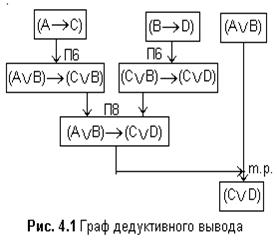
· F₁=(A®C) - посылка;

· F₂=(AÚB)®(CÚB) - заключение по F₁ и или правилу П6;

· F₃=(B®D) - посылка;

· F₄=(CÚB)®(CÚD) - заключение по F₃ и правилу П6;

· F₅=(AÚB)®(CÚD) заключение по F₂ и F₄ и правилуП8;

· F₆=(AÚВ) - посылка;

· F₇=(CÚD) - заключение по F₅ и F₆ и правилу m. p..

Так доказана истинность (CÚD).

Процесс дедуктивного вывода удобно проследить на графе, вершинами которого являются формулы, а дугами – отношения

 

Пример: доказать истинность заключения:

(A®B)&(C®D); (D&B®E); ù E

ùC ÚùA.

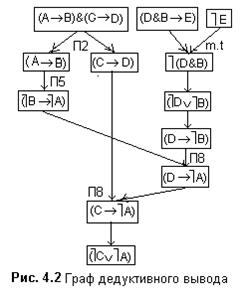
Ниже показан процесс дедуктивного вывода заключения.

· F₁=(D&B®E) - посылка;

· F₂=ùE - посылка;

· F₃=ù(D&B) - заключение по F₁ и F₂ и правилу m. t.;

· F₄=(А®В)&(С®D) - посылка;

· F₅=(A®В) - заключение по F₄ и правилу П2;

· F₆=(С®D) - заключение по F₄ и правилу П2;

· F₇=(ùB®ùA) - заключение по F₅ и правилу П2;

· F₈=(ùDÚùB) - заключение по F₃ и закону де Моргана;

· F₉=(D®ùB) - заключение по F₈;

· F₁₀=(D®ù A) - заключение по F₇ и F₉ и правилу П8;

· F₁₁=(С®ù A) - заключение по F₆ и F₁₀ и правилу П8;

· F₁₂=(ùСÚù A) - заключение по F_II.

 

Пример: доказать истинность заключения:

((A Ú B)® С); (С®(D Ú M)); (M®N); ((ù D)&(ù N))

ù A.

· F₁=((ù D)&(ù N)) - посылка;

· F₂=ùN - заключение по F₁ и правилу П2;

· F₃=(M®N) - посылка;

 

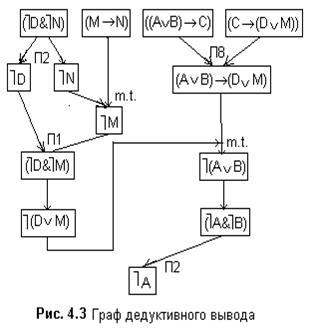
· ùM - заключение по F₂ и F₃ и правилу m.t;

· F₅=ùD - заключение по F₁ и правилу П2;

· F₆=(ùD)&(ùM) - заключение по F₄ и F₅ и правилу П1;

· F₇=ù(DÚМ) – заключение по F₆; заключение по формуле F₆ и закону де Моргана;

· F₈=((AÚB)®C) - посылка;

· F₉=(С® (DÚМ)) - посылка;

· F₁₀=((AÚB)®(DÚM)) - заключение по F₈ и F₉ и правилу П8;

· F₁₁=ù(AÚB) - заключение по F₇ и F₁₀ и правилу m.t.;

· F₁₂=(ùА)&(ùB) - заключение по F₁₁ и закону де Моргана;

· F₁₃=ùA - заключение по F₁₂ и правилу П2.

Примеры показывают, что правила вывода обеспечивают ло­гическую последовательность в преобразовании формул, каждая из которых есть либо посылка, либо промежуточный результат, либо заключение.

Принцип резолюции

Существует эффективный алгоритм логического вывода - принцип резолюции. Он основан на том, что выводимость формулы В из множества посылок и аксиом F₁; F₂; F₃;... F_n равносильна доказательству теоремы

|¾(F₁&F₂&F₃&...&F_n®B);

|¾(ù(F₁&F₂&F₃&...&F_n)ÚB);

|¾ù(F₁&F₂&F₃&...&F_n&ù B).

Из последней формулы следует, что заключение В истинно тогда и только тогда, когда формула (F₁&F₂&F₃&...&F_n&(ùB))=л. Так как все формулы связаны логической связкой конъюнкции, то это справедливо при значении “л” хотя бы одной из подформул F_i илиùB.

Для анализа формулы (F₁&F₂&F₃&...&F_n&ùB) все подформулы F_i иùB должны быть приведены к КНФ.

Два дизъюнкта КНФ, содержащие пропозициональные переменные с противоположными знаками формируют третий дизъюнкт - резольвенту, из которой будут исключены контрарные переменные. Многократно применяя эту процедуру к множеству дизъюнктов формулы (F₁&F₂&F₃&...&F_n&ùB), стремятся получить пустой дизъюнкт. Наличие пустого дизъюнкта свидетельствует о выполнении условия (F₁&F₂&F₃&...&F_n&ùB)=л. Следовательно, В является выводимой из множества заданных посылок и аксиом.

Алгоритм вывода по принципу резолюции:

Шаг 1: принять отрицание заключения, т.е. ù В;

Шаг 2: привести все формулы посылок и отрицания заключения к конъюнктивной нормальной форме;

Шаг 3: выписать множество дизъюнктов всех посылок и отрицания заключения: K = {D₁; D₂;... D_k };

Шаг 4: выполнить анализ пар множества K по правилу:

“если существуют дизъюнкты D_i и D_j, один из которых (D_i) содержит пропозициональную переменную А, а другой (D_j) - контрарную ей переменную ùА, то соединить эту пару логи­ческой связкой дизъюнкции (D_i Ú D_j) и сформировать новый дизъюнкт - резольвенту, исключив контрарные литеры А и ùА; резольвенту включить в множество К,;

Шаг 5: если в результате соединения дизъюнктов, содержащих контрарные предикаты, будет получена пустая резольвента (пустой дизъюнкт) - , то конец (доказательство подтвердило противоречие), иначе включить резольвенту в множество дизъюнктов K и перейти к шагу 4; по закону идемпотентности любой дизъюнкт и любую резольвенту КНФ можно использовать неоднократно.

 

Пример: доказать истинность заключения

(A&B®С); (C&D® ù M);(ù N® D&M)

A&B®N.

· A&B®C=ù(A&B)ÚC=(ùAÚùBÚC) – посылка (один дизъюнкт);

· C&D®ùM=ù(C&D)ÚùM=(ùCÚùDÚùM) –посылка (один дизъюнкт);

· ùN®D&M=ù(ùN)ÚD&M=(N Ú D)&(N Ú M) – посылка (два дизъюнкта);

· ù((A&B)®N)=A&B&ùN - отрицание заключения (три однолитерных дизъюнкта);

· множество дизъюнктов:

K={(ùAÚùBÚC); (ùCÚùDÚùM); (NÚD); (NÚM); A; B;ùN};

· (MÚN)ÚùN=М - резольвента;

· множество дизъюнктов:

K₁={(ùAÚùBÚC); (ùCÚùDÚùM); (NÚD); (NÚM); A; B; M; ùN};

· (ùCÚùDÚùM)ÚM =(ùCÚùD) - резольвента;

· множество дизъюнктов:

K₂={(ùAÚùBÚC); (ùCÚùDÚùM); (NÚD); (NÚM);A; B; M;ùN; (ùCÚùD)};

· (ùAÚùBÚC)Ú(ùCÚùD) =(ùAÚùBÚùD) – резольвента;

· множество дизъюнктов:

K₃={(ùAÚùBÚC); (ùCÚùDÚùM); (NÚD); (NÚM); A; B; M; ùN; (ùCÚùD); (ùAÚùBÚùD)};

· (ùAÚùBÚùD)ÚA=(ùBÚùD) - резольвента;

· множество дизъюнктов:

K₄={(ùAÚùBÚC); (ùCÚùDÚùM); (NÚD); (NÚM); A; B; M; ùN; D; (ùCÚùD); (ùAÚùBÚùD)}; (ùBÚùD) };

· (ùBÚùD)ÚB=ùD - резольвента;

· множество дизъюнктов:

K₅={(ùAÚùBÚC); (ùCÚùDÚùM); (NÚD); (NÚM); A; B; M; ùN; D; (ùCÚùD); (ùAÚùBÚùD)}; (ùBÚùD); ùD};

· ùDÚ(NÚD)=N - резольвента;

· множество дизъюнктов:

K₆={(ùAÚùBÚC); (ùCÚùDÚùM); (NÚD); (NÚM);A; B; M; ùN; D; (ùCÚùD); (ùAÚùBÚùD)}; (ùBÚùD); ùD}; N};

· NÚù N = - пустая резольвента.

Для демонстрации удобно исполь­зовать граф типа дерево, корнем которого является один из дизъюнктов отрицания заключения, а вершинами – дизъюнкты всех посылок и отрицания заключения. Узлами графа типа дерево являются резольвенты.

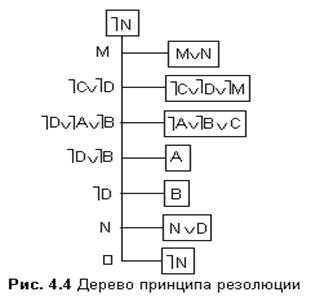
Так доказана истинность заключения (A&B®N).

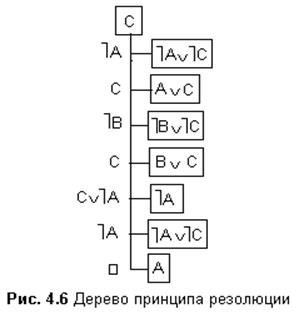
Пример: доказать истинность заключения

(A®B)&(C®D); (D&B®M);ù M

(ùAÚùC).

· (A®B)&(C®D)=(ùAÚB)&(ùCÚD) - посылка;

· D&B®M=ù(D&B)ÚM=(ùDÚùBÚM) - посылка;

· ùM - посылка;

· (ù AÚ ù C) = A &C - отрицание заключения;

· множество дизъюнктов:

K ={A; C; ùM; (ùAÚB); (ùCÚD); (ùDÚùBÚM)};

· AÚ(ùAÚB)=B - резольвента;

· множество дизъюнктов:

K ={A; C; ùM; (ùAÚB); (ùCÚD); (ùDÚùBÚM); B};

· BÚ(ùDÚùBÚM)=(ùDÚM) - резольвента;

· множество дизъюнктов:

K ={A; C; ùM; (ùAÚB); (ùCÚD); (ùDÚùBÚM); B; (ùDÚM)};

· (ùDÚM)Ú(ùCÚD)=(ùCÚM) - резольвента;

· множество дизъюнктов:

K ={A; C; ùM; (ùAÚB); (ùCÚD); (ùDÚùBÚM); B; (ùDÚM); (ùCÚM)};

· (ùCÚM)ÚùM=ùC - резольвента;

· ùCÚC=ÿ - пустая резольвента.

Так доказана истинность заключения (ùAÚùC).

 

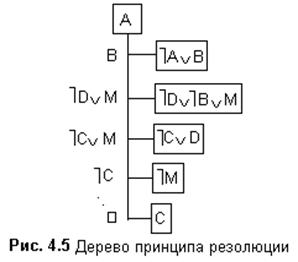
Пример: доказать истинность заключения

((ùАÚùBÚùА &ùB)®С); ((AÚBÚА&B)®ùC)

(C®ùA).

· ((ùАÚùBÚùА &ùB)®С)= (АÚC)&(BÚC) - посылка;

· (AÚBÚА&B)®ùC)= (ùАÚùC)&(ùBÚùC) -посылка;

· ù(C®ùA)=C&А – отрицание заключения;

· множество дизъюнктов:

K={(АÚC); (BÚC); (ùАÚùC); (ùBÚùC); C; А };

· СÚ(ùАÚùC)=ùА – резольвента;

· множество дизъюнктов:

K₁={(АÚC); (BÚC); (ùАÚùC); (ùBÚùC); C; А; ùА };

· ùАÚ(АÚC)=C – резольвента;

· множество дизъюнктов:

K₂={(АÚC); (BÚC); (ùАÚùC); (ùBÚùC); C; А; ùА };

· СÚ(ùBÚùC)=ùB –резольвента;

· множество дизъюнктов:

K₃={(АÚC); (BÚC); (ùАÚùC); (ùBÚùC); C; А; ùА; ùB };

· ùBÚ(BÚC)=C – резольвента;

· множество дизъюнктов:

K₄={(АÚC); (BÚC); (ùАÚùC); (ùBÚùC); C; А; ùА;ùB};

· CÚùA=(CÚùA) – резольвента;

· множество дизъюнктов:

K₅={(АÚC); (BÚC); (ùАÚùC); (ùBÚùC); C; А; ùА; ùB; (CÚùA)};

· (CÚùA)Ú (ùАÚùC)=ùА – резольвента;

· множество дизъюнктов:

K₅={(АÚC); (BÚC); (ùАÚùC); (ùBÚùC); C; А; ùА; ùB; (CÚùA)};

· (CÚùA)Ú (ùАÚùC)=ùА – резольвента;

· ùАÚA= - пустая резольвента.

 

Так доказана истинность заключения (C®ùA).

Так как резольвенты включаются в множество дизъюнктов K, то возможно их неоднократное использование в процессе вывода. Многократное использование дизъюнктов оправдано законом идемпотентности, т.к. D_i=D_i&D_i&...&D_i.

Достоинством принципа резолюции является то, что при доказательстве истинности заключения применяют только одно правило: поиск и удаление контрарных пропозициональных переменных на множестве дизъюнктов до получения пустой резольвенты.

Логика предикатов

Если объект высказывания, т.е. то, о чем говорится в предложении, не определен, то это предложение называют высказывательной функцией. Аргументами высказывательной функции являются предметные переменные и предметные постоянные, которые обозначают строчными буквами латинского алфавита {х, у,z...} и {а, в, с, ¼}соответственно. Высказывательная функция приобретет значение "и" или "л" только при подстановке вместо предметных переменных их постоянных значений.

Высказывательную функцию иначе называют предикатом (лат. praedicatum - логическое сказуемое).

Например,

а) если на множестве натуральных чисел задать высказывательные функции:

Р₁(x):= "x - простое число",

P₂(6, y):="y меньше 6",

P₃(6, y, z):="z есть частное от деления числа 6 на y",

где z и y есть предметные переменные (целые числа), а 6 – предметная постоянная (целое число), то высказываниями будут

P₁(3) = и, P₁(4) = л,

P₂(6,2) = и, P₂(6,7) = л,

P₃(6,2,3) = и, P₃(6,2,5) = л,

б) если на множестве имен индивидов, университетов и специальностей задать высказывательные функции или предикаты

P₄(x):="х - студент",

P₅(x, КГТУ):="студент х университета КГТУ",

P₆(x, y, прикладная информатика):= "студент x университета y, обучающийся по специальности "прикладная информатика””,

где x и y есть предметные переменные, а КГТУ и “прикладная информатика” – предметные постоянные, то высказываниями будут

P₄(Петров) = и, P₄(Сидоров) = л,

P₅(Петров, КГТУ) = и, P₅(Сидоров, КГТУ) = л,

P₆(Петров, КГТУ, "прикладная информатика") = и,

P₆(Сидоров, КГТУ, "прикладная информатика") = л.

Для ограничения области определения предметных переменных вводят операторы, которые называют кванторами.

Суждение, в котором утверждается или отрицается наличие каких-либо признаков или отношений у части переменных области определения, называют частным суждением. Как правило, эти суждения на естественном язы­ке выражают словами "несколько", "часть" и т.п. Для формализации таких суждений используют логическую операцию, ограничивающую область определения предиката. Оператор, ограничивающий область определения. по­лучил название квантора существования, который обозна­чают “$_x”. Предикат записывают после квантора существования в круглых скобках $_x(Р_n(x)). На естественном языке эта запись означает: “существуют такие элементы х, что Р_n(х) истинно".

Если частное суждение распространяется на несколько предметных переменных, то перед предикатом записывают кванторы существования для всех предметных переменных, по которым есть частное суждение, т.е. $_x $_y $_z...(P_n(x, y, z,...)).

Например, $_x(P₁(x)):= "cуществуют целые числа, которые являются простыми". Это условие выделяет на множестве целых чисел подмножество X = {2, 3, 5, 7, 11,..}, для которого предикат P₁(x) принимает значение “и”.

$_y(P²₂(6,y)):="существуют числа y, которые меньше 6". Это условие выделяет на множестве целых чисел подмножество Y= {1, 2, 3, 4, 5}, для которого предикат P₂(6,y) принимает значение “и”.

$_z(P³₃(6,2,z)):="существует число z, которое является частным от деления 6 на 2". Это условие выделяет на множестве целых чисел единственное число Z=3, для которого предикат P₃(6,2,z) принимает значение “и”.

Если P₇(x):="x имеет зачетную книжку", то $_x(P₄(x)&ùP₇(x)):= "существуют студенты (x), которые не имеют зачетной книжки"; $_x$_y(P²₅(x,y)&ùP₇(x)):="существуют студенты (x) некоторых университетов (y), которые не имеют зачетной книжки" и т.п..

Суждение, в котором утверждается или отрицается наличие каких-либо признаков или отношений для всех переменных области определения, называют общими суждениями. Как правило, эти сужде­ния в естественном языке отмечают словами "все", "каждый", "любой" и т.п. Для формализации этих суждений используют логическую операцию над всей областью определения предиката. Оператор этой логической операции получил название квантора всеобщности, который обозначают "_x. Предикат записывают после квантора всеобщности в круглых скобках.

"_x(Р_n(x)). На естественном языке эта формальная запись означает: “для всех х значение Р_n(х) истинно“.

Если общее суждение распространяется на несколько предметных переменных, то перед предикатом записывают кванторы всеобщности для всех предметных переменных, по которым есть общее суждение, т.е.

"_x "_y "_z... (P_n(x, y, z,...)).

Например, "_x(P₄(x)&P₇(x)):= "все студенты (x) имеют зачетную книжку";

"_x"_y(P₅(x,y)&P₇(x)):="все студенты (x) всех университетов (y) имеют зачетную книжку";

"_x(P³₆(x, КГТУ, "прикладная информатика")&P₇(x)):= "все студенты (x) университета КГТУ, обучающиеся по специальности "прикладная информатика", имеют зачетную книжку";

"_x"_z(P³₆(x, КГТУ, z)&P₇(x)):= "все студенты (x) университета КГТУ, обучающиеся на всех специальностях (z), имеют зачетную книжку";

"_x"_y"_z(P³₆(x,y,z)&P₇(x)):= "все студенты (x) всех университетов (y), обучающиеся на всех специальностях (z), имеют зачетную книжку".

Существуют предикаты, для которых область определения по различным предметным переменным ограничивают различными кванторами.

Например,

"_x$_y(P²₂(x, y)):= "для всех целых чисел x существует меньшее число y".

"_x"_y$_z(P³₃(x, y, z)):="для всех целых чисел x и y существует число z, которое является частным от деления x на y".

Предметную переменную предиката, если по меньшей мере одно ее вхождение связано квантором, называют связанной переменной. Предметную переменную предиката, если все ее вхождения в формулу свободны от квантора, называют свободной переменной.

Например,

$_y(P²₂(x,y)):="для всех целых чисел x существуют меньшие числа y". В этом примере x – свободная, а y –связанная переменные.

$x "z(P³₆(x,y,z)&ùP₇(x)):= “есть студенты университета, которые не имеют зачетной книжки”. В этом примере x и z –связанные, а y –свободная переменные.

$_x "_y (Р²₁ (x; y) ® "_z (Р₂(z)) все пред­метные переменные связаны.

"_z (Р₁(z)&$_x(Р²₂(x; z))®(Р²₂(z; y)Ú(Р²₂(x; z)) предметные переменные x и z связанные, а y – свободная.

Cвободная переменнная есть переменная вне текущей процедуры, а связанная переменная есть локальная переменная для текущей процедуры.

Если высказывательная функция содержит один аргумент, то задан одноместный предикат, если она содержит n аргументов, то n-местный предикат. Одноместный предикат, как правило, описывает наличие какого-либо признака у предмета, а n-местный предикат – наличие отношений между n предметами.

Между элементами области определения может быть задана некоторая структура или функциональные отношения. Тогда функциональный символ f(x₁, x₂,...x_n) указывает на задание этой структуры между предметными переменными и/или предметными постоянными.

Например, дату можно рассматривать как структуру, заданную на предметных переменных: число, месяц и год. В этом случае функциональным символом является “дата”, а аргументами число, месяц и год, т.е. “дата (число, месяц, год)”. Для предметных постоянных эта структура формирует выражение (например, “дата (1 января 2001)”). Описание треугольника также можно рассматривать как структуру на предметных переменных, описывающих координаты вершин треугольника. Тогда функциональным символом является “треугольник”, а аргументы этой функции следующие: вершина (координаты x₁, y₁), вершина (координаты x₂, y₂), вершина(координаты x₃, y₃).

Алгебра предикатов

Множество T ={T₁, T₂, T₃, T₄}, включающее множества предметных переменных Т₁= {x, y, z,..}, предметных постоянных Т₂= {a, b, c,...}, функциональных символов Т₃={f₁, f₂, f₃,...} и предикатных символов Т₄=(P₁, P₂, P_3,...} с заданными операциями F ={ù; &; Ú; ®; «; "; $} формируют алгебру предикатов, т.е.

A_п=< T; F >.

Любую предметную переменную и предметную постоянную в алгебре предикатов называют термом и обозначают символом t_i.

Если f_i - функциональный символ и t₁, t₂,..t_n - термы, то f_i(t₁, t₂,..t_n) также есть терм, где n –число аргументов функции, i –индекс функции.

Никаких иных термов нет.

Если P_i –предикатный символ и t₁, t₂,..t_n - термы, то F= P_i(t₁, t₂,..t_n) - элементарная формула.

Если F₁ и F₂ формулы, то (ùF₁ ); (F₁ &F₂); (F₁ÚF₂); (F₁®F₂);(F₁«F₂) также формулы.

Если F формула, a x - предметная переменная, входящая в атомы формулы F, то "_x(F)и $_x(F) также формулы.

Никаких иных формул нет.

Для формирования сложных формул используют вспомогательные символы “(“ и “)”.

Простейшими опера­циями так же, как в исчислении высказываний, являются отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.

Отрицание (ùF(t₁; t₂;¼ t_n)) есть одноместная операция, посредством которой из данной формулы F(t₁; t₂;¼ t_n) полу­чают ее отрицание.

Пример: если Р² (х; a):= "х находится на a " и a =”стол”, то выводимы формулы:

а) "_x(ù Р² (х; a)):= "для всех х верно, что х не находится на a “;

b) ù "_x(Р² (х; a)):= "не для каждого х верно, что х находит­ся на a ”;

c) ù $_x(Р² (х; a)):= “не существует х, для которого верно, что х находится на a ”.

Конъюнкция (F₁(t₁₁; t₁₂;..t_1n)&F₂(t₂₁; t₂₂;..t_2n)) есть двуместная операция, посредством которой из формул F₁ и F₂ получают новую формулу F (t₁₁; t₁₂;¼ t_1n; t₂₁; t₂₂;¼ t_2n ) с числом предметных переменных и постоянных, равным объединенному числу их в исходных формулах. Значение формулы истинно тогда и только тогда, когда истинны обе форму­лы F₁ и F₂.

Пример: если P₁(х):=“выдающийся музыкант” и

P₂(х):= "талантливый писатель”, то выводимы формулы:

а) $_x(P₁(х))&$_x(P₂(х)):= ”существуют выдающиеся музыканты и существуют талант­ливые писатели";

b) $_x(P₁(х)&P₂(х)):= ”существуют лица, являю­щиеся талантливыми писателями и выдающимися музыкантами”.

Пример: если х - предметная переменная (индивид), ‘a’ - предметная постоянная (например, Саша) и P₁ (х; a):=”х дру­жит с ‘a’”, P₂. (х; a):=“х встретил ’a’ ”, то выводимы фор­мулы:

а) $_x(P₁.(х; a)&P₂.(х; a)):= “Саша встретил друга”;

b) $_x(ù P₁.(х; a)&P₂.(х; a)):=“Саша встретил недруга”;

c) ù"_x(P₁.(х; a)&P₂.(х; a)):= “не каждый встречный есть друг Саши”;

d) $_x(P₁.(х; a)&(ùP₂.(х; a))):= “есть друзья, с которыми Саша не встречается”.

Дизъюнкция (F₁(t₁₁; t₁₂;..t_1n)ÚF₂(t₂₁; t₂₂;..t_2n)) есть двуместная операция, посредством которой из формул F₁ и F₂ получают новую формулу F (t₁₁; t₁₂;¼ t_1n; t₂₁; t₂₂;¼ t_2n ) с числом предметных переменных и постоянных, равным объединенному числу их в исходных формулах. Значение формулы ложно тогда и только тогда, когда ложны обе формулы F₁ и F₂.

Пример: если предметные переменные х, у - города России и P²₁.(х; y):= “переезд из х в у поездом”; P²₂.(х;y):= “переезд из х в у самолетом”; P²₃.(х; y):= “переезд из х в у автобусом”, то выводимы формулы:

a) "_x"_y(P²₁.(х; y)ÚP²₂.(х; y)ÚP²₃.(х; y)):= “для всех городов России возможен переезд поездом, автобусом или самолетом”;

b) ù"_x$_y(P²₁. (х; y)Úù P²₂. (х; y)Úù P²₃. (х; y)) - "не для всех городов x существуют города y, между которыми невозможен переезд автобусом или самолетом, но возможен поездом”.

Импликация (F₁(t₁₁; t₁₂;..t_1n)®F₂(t₂₁; t₂₂;..t_2n)) есть двухместная операция, посредством которой из формул F₁и F₂ получают новую формулу F(t₁₁; t₁₂;..t_1n; t₂₁; t₂₂;..t_2n ) с числом предметных переменных и постоянных, равным объединенному числу их в исходных формулах. Значение формулы ложнотогда и только тогда, когда F₁ истинно, а F₂ - ложно.

Пример: если х - предметные переменные для индивида, P₁(x):= "быть судьей", P₂(x):= "быть юристом", то выводимы формулы:

a) "_x(P₁(x)®P₂(x)):= "все судьи - юристы";

b) ù"_x(P₂(x)®P₁(x)):= "неверно, что все юристы - судьи",

Пример: если х-предметная переменная для индивида и P₁(x):="x принадлежит к большинству", а P₂(x):= "x стремится к миру", то выводима формула:

$_x(P₁(x)&P₂(x))&"_x(P₁(x)®P₂(x)):= “большинстволюдей стремится к миру".

Эквиваленция (F₁(t₁₁;t₁₂;..t_1n)«F₂(t₂₁; t₂₂;..t_2n)) есть двумест­ная операция, посредством которой из формул F₁ и F₂ получают новую формулу F (t₁₁; t₁₂;¼ t_1n; t₂₁; t₂₂;¼ t_2n ) c числом предметных переменных и постоянных, равным объединенному числу их в исходных формулах. Значение формулы истинно тогда и только тогда, когда обе формулы F₁ и F₂ имеют одно и то же значение истины или лжи.

Пример: если х - предметная переменная, Р(х) - предикат, то выводимы формула $_x(P(x))«ù"x(ùP(x)):= формула: "суще­ствует переменная х, для которой Р(х) истинно” эквивалентна формуле: “не для всех х Р(х) ложно".

Рассмотренные логические операции позволяют формализовать с помощью термов, предикатов и кванторов внутреннюю структу­ру предложения и формировать сложные суждения.

 

Пример: дано cуждение “некоторые действительные числа являются рациональными”. В этом суждении есть два предиката P₁(x):=”x - действительное число” и P₂(x):=”x - рациональное число”. Тогда формула этого суждения должна быть записана так: F=$_x(P₁(x)&P₂(x)).

Ошибочными являются эквивалентные формулы F=$_x(P₁(x)®P₂(x)) и F=$_x(ùP₁(x)ÚP₂(x)), так как первое суждение ”некоторые числа, если они действительные, то они рациональные”, не эквивалентно суждению “некоторые числа не являют

⇐ Предыдущая16171819202122232425Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: