Операция прямого произведения

r’={t’|$_x$_y(r₁(x)&r₂(y)&(t’[1]=x[1])&(t’[2]=x[2])..&(t’[n₁]=x[n₁])&

(t’[n₁+1]=y[1]) &(t’[n₁+2]=y[2]).. &(t’[n₁+n₂]=y[n₂]))}.

Кванторы существования используют потому, что каждый кортеж второго отношения должен быть приписан к каждому кортежу первого отношения.

 

Операция естественнного соединения

r’={t’|$_x$_y(r₁(x)&r₂(y)&(x(A_i)=y(A_j))&(t’[1]=x[1])&..(t’[i]=x[i]=y[j])&..

&(t’[n₁]=x[n₁])&(t’[n₁+1]=y[1])&(t’[n₁+2]=y[2])..&(t’[n₁+n₂-1]= y[n₂]))}.

 

Операция q-соединения

r’={t’|$_x$_y(r₁(x)&r₂(y)&(x(A_i)qy(A_j))&(t’[1]=x[1])&..(t’[i]=x[i])&..

&(t’[n₁]=x[n₁])&(t’[n₁+1]=y[1])&..&(t’[n₁+j]=y[j])..&(t’[n₁+n₂]= y[n₂]))}.

 

Языки реляционной логики

Основная структура языков реляционной логики также отвечает схеме

<заключение>:-

<условие>{“,”<условие>}.

<заключение> есть схема формируемого отношения, а <условия> включают перечень используемых отношений и алгебраические выражения, определяющий истинное значение формулы для свободных переменных-кортежей.

Одним из таких языков является язык SQL (Structured Query Language), используемый в системах управления реляционными базами данных.

Синтаксическую структуру запроса на языке SQL можно представить инструкцией:

 

SELECT <список атрибутов>

FROM <список отношений>

WHERE <предикат >, где

<список атрибутов>:=<АТРИБУТ>{“,”<АТРИБУТ>};

<список отношений>:=<отношение>{“,”<отношение>};

<предикат >:=<алгебраическое выражение условия>.

 

Первая строка инструкции - оператор SELECT - формирует схему формируемого отношения rel(r’), что в реляционной алгебре исполняет оператор p_rel(r₁). Вторая строка - оператор FROM – указывает список используемых отношений. Третья строка - оператор WHERE – оформляет условия для извлечения свободных переменных-кортежей из формулы F(t), что в реляционной алгебре исполняет оператор d_B(r₁). При формировании условий могут быть использованы логические связки.

Порядок атрибутов в формируемом отношении определяется порядком в <списке атрибутов>, а порядок кортежей в формируемом отношении управляется с помощью оператора ORDER BY, после которого стоит имя атрибута и ключевое слово ASC (сортировка по возрастанию) или DESC (сортировка по убыванию):

SELECT <список атрибутов>

FROM <список отношений>

ORDER BY <ИМЯ _АТРИБУТА> ASC.

или ORDER BY <ИМЯ _АТРИБУТА> DESC.

 

Пример.

SELECT A1, A2, A3 FROM r1	r’1	A1	A2	A3
	a1	b1
ORDER BY A3 ASC.		a3	b3
		a2	b2
		a4	b1
	r’	A1	A2	A3
SELECT A1, A2, A3		a2	b2
FROM r1		a4	b1
ORDER BY A3 DESC.		a3	b3
		a1	b1

 

Чтобы в результирующем отношении не было дубликатов кортежей нужно после SELECT писать ключевое слово UNIQUE.

Если используется несколько отношений, то при описании атрибута нужно указывать <имя_отношения>”.”<имя_атрибут>.

Например, SELECT r₁.A₁, r₃.A₄

Синтаксическая структура бинарных операций UNION, MINUS, (DIFFERENCE), INTERSECTION на языке SQL имеет следующий вид:

 

SELECT <список атрибутов> SELECT <список атрибутов>

FROM <отношение> FROM <отношение>

[WHERE <предикат >] [WHERE <предикат >]

UNION MINUS

SELECT <список атрибутов> SELECT <список атрибутов>

FROM <отношение> FROM <отношение>

[WHERE <предикат >]. [WHERE <предикат >].

Синтаксическая структура операции естественного соединения (JOIN) на языке SQL имеет следующий вид:

 

SELECT <список атрибутов>

FROM <отношение_1>INNER JOIN <отношение_2>

ON<отношение_1>”.”<атрибут><оператор_сравнения><отношение_2>”.”<атрибут>.

Синтаксическая структура операции q- соединения (q- JOIN) на языке SQL имеет следующий вид:

 

SELECT <список атрибутов>

FROM <отношение_1>INNER JOIN <отношение_2>

ON<отношение_1>”.”<атрибут><оператор_сравнения><отношение_2>”.”<атрибут>.

WHERE <предикат>.

Часто используют в операторе WHERE вложенные подзапросы, которые генерируют промежуточные отношения. На это указывает оператор IN, используемый для выяснения принадлежности элемента множеству.

 

SELECT<список атрибутов>

FROM <список отношений>

WHERE <предикат> IN

SELECT<список атрибутов>

FROM<список отношений>

WHERE<предикат>.

Вложенный подзапрос генерирует множество кортежей непоименованного отношения, которое было динамически создано и может отличаться от любого хранимого отношения. Поскольку это отношение непоименовано, оно может использоваться только в том месте, в котором оно появляется в подзапросе; к такому отношению невозможно обратиться по имени из какого-либо другого места запроса.

Операции, которые можно применить к подзапросу, основаны на тех операциях, которые можно применить к множеству:

x IN U – x принадлежит множеству U, т.е. xÎU;

x NOT IN U – x не принадлежит множеству U, т.е. xÏU;

При использовании оператора IN неявно применяется квантор существования, т.е. “WHERE x IN P” эквивалентно “$_x(P(x))”.

Использование оператора NOT IN – эквивалентно применению квантора всеобщности, т. е. “WHERE x NOT IN P” эквивалентно “"_x(P(x))”.

Некоторые операции языка SQL основаны на арифметических действиях с целыми числами, а именно:

COUNT (U) – количество элементов множества U, т.е. |U|.

SUM(U) – сумма всех элементов множества U;

MAX(U) – максимальный элемент множества U;

MIN(U) – минимальный элемент множества U;

AVG(U)= SUM(U)/COUNT(U) – среднее значение элемента множества U.

Операции COUNT, SUM, MAX, MIN и AVG являются встроенными функциями, их результатом является число.

Синтаксическая структура этих операций на языке SQL имеет вид:

SELECT COUNT<атрибут>|SUM<атрибут>|MAX<атрибут>|

MIN<атрибут>| AVG<атрибут>

FROM <список отношений>

WHERE <предикат>.

Нечеткая логика

Основные понятия и характеристики нечетких множеств, отображений и отношений были изложены в 1.1.2, 1.2.2 и 1.3.2, а алгебраические операции над ними в 1.7. Поэтому в настоящем разделе рассмотрены только проблемы и правила вывода в нечетком исчислении высказываний.

Нечеткое исчисление

Нечеткие высказывания есть предложения А’, степень истинности r(А’) или ложности ùr(А’) которых также принимает значение на интервале [0; 1]. Например, высказывание: “сегодня хорошая погода”. По каким признакам и кто дал такую оценку? Ведь “у природы нет плохой погоды...”.

Нечеткие предикаты есть высказывательные функции, аргументами которых являются предметные переменные и предметные постоянные. Степень истинности предметных переменных и высказывательных функций также принадлежит интервалу [0; 1].

Например, высказывание “Петров выполняет ответственное задание”. Как понимать “ответственное задание”?

Л ингвистические переменные. Как правило, нечеткими предметными постоянными и переменными являются слова и словосочетания естественного языка. Лингвистическая переменная служит для качественного описания явления, факта или события. Множество лингвистических переменных, описываемых также лингвистической переменной, называют терм-множеством и обозначают Т(x).

Так терм-множества ”возраст”, ”количество”, ”частота”, “расположение” и т. п. могут быть представлены лингвистическими переменными:

T’₁(“возраст”)={ ребенок, подросток, юноша, молодой человек, человек средних лет, пожилой человек, старик,...};

T’₂(”количество”)={ малое, среднее, большое,...};

T’₃(“частота”)={почти всегда, часто, редко, иногда, почти_никогда...};

T’₄(“расположение”)={вплотную; близко, рядом, далеко,...}.

Для того, чтобы согласовать мнения различных экспертов, степень истинности лингвистической переменной удобно определять по значению функции принадлежности этой переменной какому-то интервалу. Это позволит для каждого конкретного факта или события количественно оценивать ее значение в конкретном высказывании.

Нечеткие формулы. Для формирования сложных высказываний используют логические связки отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции. Так формируются нечеткие логические формулы.

Степень истинность сложного высказывания определяется как степень принадлежности результатов исполнении операций над нечеткими множествами:

r(ùA’)=(1 - r (A’));

r(A’&B’)=min{r(A’); r(B’)};

r(A’ÚB’)=max{r(А’); r (B’)};

r(A’®B’)=max{(1-r(А’)); r (B’)};

r(A’«B’)=min{max{(1-r(А’)); r (B’)}; max{(1-r(B’)); r (A’)}}.

Следует обратить внимание, что законы противоречия и “третьего не дано” для нечетких высказываний не выполняются.

Так для четких высказываний: r(A&ùA)=л, r(AÚùA)=и, а для нечетких высказываний:

r(A’&ùA’)=min{r(A’); (1-r(A’))}, r(A’ÚùA’)=max{r(А’); (1-r(ùA))}.

Нечеткие правила вывода. Так же как в логике четких высказываний, в логике нечетких высказываний выводима теорема:

|¾F₁’&F₁’&..& F₁’®B’.

Для нечетких высказываний это удобно пояснить на формировании заключения с помощью условного нечеткого высказывания “если A’, то B’, иначе С’”.

Очевидно, что нечеткое высказывание “если A’, то B’” можно определить как нечеткое отношение между нечеткими высказываниями A’ и B’, т. е. (А’ÄB’), а нечеткое высказывание “если не А, то С” – как нечеткое отношение между высказываниями ùA’ и С’. Объединение этих двух отношений есть формула условного нечеткого высказывания:

((A’®В’), C’) = ((А’ÄB’)È(ùA’ÄC’)).

Если даны значения степеней истинности нечетких высказываний r(A’), r(B’) и r(C’),, то истинность высказывания “если A’, то B’ иначе C’” может быть определена, как для нечетких отношений, по формуле: r((A’ ® В’), C’) = max{min{r(A’), r(B’)}; min{r(ùA’), r(C’)}}.

 

Пример: “Если сегодня вечером будет дождь, то завтра будет солнечная погода иначе завтра будет пасмурный день”.

Пусть для высказывания A’:=”сегодня вечером будет дождь” r(A’)=0,3, для высказывания B’=”завтра будет солнечная погода”- r(B’)=0,5, для высказывания C’:=”завтра будет пасмурный день”- r(C’)=0,2.

Следовательно,

r((A’®В’), C’)= max{min{r(A’), r(B’)}; min{r(ùA’), r(C’)}}=

max{min{0,3; 0,5}; min{0,7; 0,2}= max{0,3; 0,2}=0,3.

Если r(C’)=1, т.е. высказывание C’ истинно для любых значений истинности высказывания ùA’, то формула условного высказывания принимает вид, т.е. ((А’ÄB’)ÈùA’), что соответствует высказыванию “если A’, то B’”

Степень истинности такого высказывания есть

r(A’®В’)= max{min{r(A’), r(B’)}; r(ùA’)}.

Так можно определить истинность импликации по известным значениям истинности посылки A’ и заключения B’.

Пример: “Если сегодня вечером будет дождь, то завтра будет солнечная погода”.

Пусть для высказывания A’:=”сегодня вечером будет дождь” r(A’)=0,3, для высказывания B’=”завтра будет солнечная погода” принято r(B’)=0,5.

Следовательно,

r(A’®В’)= max{min{r(A’), r(B’)}; r(ùA’)}=max{min{0,3, 0,5}; 0,7}=

max{0,3; 0,7}=0,7.

Если даны множества нечетких высказываний {A’=r(u_i)/u_i} и {B’=r(v_j)/v_j} о фактах {u₁, u₂, u₃, u₄, u₅, u₆} и {v₁, v₂, v₃, v₄, v₅, v₆} то истинность r(A’®В’) необходимо определять для каждой пары (u_i, v_j) по формуле: r(A’®В’)= max{min{r(u_i), r(v_j)}; ùr(u_i)}.

 

Пример: пусть даны нечеткие высказывания

r(A’)={0,6/u₁; 0,4/u₂; 0,8/u₃; 0,2/u₄; 1,0/u₅; 0,3/u₆};

r(B’)={0,9/v₁; 0,4/v₂; 1,0/v₃; 0,7/v₄; 0,3/v₅; 0,5/v₆}

Для каждой позиции таблицы r(A’®В’) нужно вычислить значение r(u_i®v_j)=max{min{r(u_i), r(v_j)}; ùr(u_i)}.

Например, r(u₄®v₂)=max{min{0,2; 0,4}; 0,8}=max{0,2; 0,8}=0,8.

Все результаты вычислений r(u_i®v_j) сведены в таблицу.

 

	v1	v2	v3	v4	v5	v6
u1	0,6	0,4	0,6	0,6	0,4	0,5
u2	0,6	0,6	0,6	0,6	0,6	0,6
u3	0,8	0,4	0,8	0,7	0,3	0,5
u4	0,8	0,8	0,8	0,8	0,8	0,8
u5	0,9	0,4	1,0	0,7	0,3	0,5
u6	0,7	0,7	0,7	0,7	0,7	0,7

 

Основным правилом вывода, как и в обычном исчислении, является modus ponens, соглас­но которому истинность заключения r(В’) определяют по обобщенной схеме этого правила:

r(A’); r (A’®В’)

r(B’)=r(A’)·r (A’®В’),

где r(A’)·r (A’®В’) – композиция нечетких высказываний A’ и (A’®В’).

В этом случае истинность высказывания B’ определяется формулой:

r(B’)= r(A’)·r(A’®В’)=max{min{r(A’); r(A’®В’)}}.

Пример: пусть r(A’®В’) задано предыдущей таблицей, а

r(A’)={0,36/u₁; 0,16/u₂; 0,64/u₃; 0,04/u₄; 1,0/u₅; 0,09/u₆}.

Тогда истинность заключения:

r(B’)=r(A’)·r(A’®В’)={max _v1{min{0,36/u₁; 0,6/(u₁,v₁)},

min{0,16/u₂; 0,6/(u₂,v₁)}, min{0,64/u₃; 0,8/(u₃,v₁)},

min{0,04/u₄; 0,8/(u₄,v₁)}, min{1,0/u₅; 0,9/(u₅,v₁)}, min{0,09/u₆; 0,7/(u₆,v₁)}}, max_v2{min{0,36/u₁; 0,4/(u₁,v₂)}, min{0,16/u₂; 0,6/(u₂,v₂)}, min{0,64/u₃; 0,4/(u₃,v₂)}, min{0,04/u₄; 0,8/(u₄,v₂)}, min{1,0/u₅; 0,4/(u₅,v₂)}, min{0,09/u₆; 0,7/(u₆,v₂)}}, max_v3{min{0,36/u₁; 0,6/(u₁,v₃)}, min{0,16/u₂; o,6/(u₂,v₃)}, min{0,64/u₃; 0,8/(u₃,v₃)}, min{0,04/u₄; 0,8/(u₄,v₃)}, min{1,0/u₅; 1,0/(u₅,v₃)}, min{0,09/u₆; 0,7/(u₆,v₃)}}...=max_v1{0,36, 0,16, 0,64, 0,04, 0,9, 0,09}, max_v2{0,36, 0,16, 0,4, 0,04, 0,4, 0,09}, max_v3{0,36, 0,16, 0,64, 0,04, 1,0, 0,09},..= {0,9/v₁, 0,4/v₂, 0,64/v₃, 0,7/v₄, 0,64/v₅, 0,5/v₆}.

Экспертные системы

Экспертная система относится к категории интеллектуальных вычислительных систем, которая использует знания специалистов о некоторой специализированной предметной области, хранит и накапливает эти знания, предлагает и объясняет решения конкректных задач на уровне профессионала. Как правило, знания профессионала сформулированы нечетко. Поэтому алгоритмического решения такие задачи не имеют.

Идеализированная экспертная система содержит пять основных компонент: базу данных и знаний, интерфейс пользователя, подсистему логического вывода, блок извлечения и пополнения знаний и блок объяснения решения.

Интерфейс служит для взаимодействия пользователя или эксперта-профессионала с компьютером на проблемно-ориентированном языке. В интерфейсе происходит трансляция предложений этого языка на внутренний язык компьютера

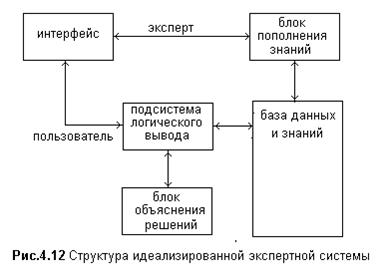
База знаний хранит и накапливает информацию о фактах, явлениях, событиях предметной области и о правилах, используемых экспертом-профессионалом при принятии решений. Правила и факты описывают на языке математической логики.

По описанию пользователем характерных признаков факта, явления или события в подсистеме логического вывода происходит отбор соответствующих правил, сравнение с характерными признаками, введенными экспертом системы. Логические методы экспертной системы имеют развитый математический аппарат для вывода новых фактов: логику предикатов и нечеткую логику. Основными процедурами вывода являются правила подстановки, унификации и заключения.

Блок объяснения решений служит для аргументации причинно-следственных связей и используемых правил решений.

Блок пополнения и корректировки базы знаний предназначен только для эксперта-профессионала, т. к. знания имеют слабо формализуемый характер по причинно-следственным связям. Поэтому самым узким местом экспертной системы является наполнение и корректировка правил базы знаний.

Одной из первых экспертных систем была система медицинской диагностики и лечения инфекционных заболеваний MYCIN. В этой системе для вывода заключения В’ по наличию одной или нескольких посылок F’ используют так называемый коэффициент уверенности КУ.

Коэффициент уверенности - это разность между мерой доверия - МДи мерой недоверия - МНД к истинности заключения:

КУ [(F’®В’): F'] = МД [(F’®В’): F’] - МНД [(F’®В’): F'],

где КУ [(F’®В’): F’] – коэффициент уверенности гипотезы (F’®В’) при ис­тинности свидетельства F’;

МД[(F’®В’): F’] - мера доверия гипотезе (F’®В’) при истинности свидетельства F’;

МНД [(F’®В’): F’] - ме­ра недоверия гипотезе (F’®В’) при истинности свиде­тельства F’.

КУ может изменяться от - 1 (абсолютная ложь) до +1 (абсолютная истина).

При наличии двух или нескольких свидетельств (F'₁ и F'₂) в системе MYCINпроисходит уточнение мер доверия и недоверия гипотезе (F’®В’) при заданных значениях истинности двух свидетельств F'₁ и F'₂ по следующему правилу:

МД [(F’®В’): F'₁, F'₂]=МД [F’₁®В’: F'₁]+

МД [F’®В’: F'₂]×(1 - МД [F’®В’: F'₁]);

МНД [(F’®В’): F’₁, F'₂]=МНД [(F’®В’): F’₁]+

МНД [(F’®В’): F'₂]×(1 - МНД [(F’®В’):F’₁]).

Смысл формулы состоит в том, что эффект второго свидетельства (F'₂) на гипотезу (F’®В’) при заданном свидетельстве F'₁ уточняет истинность гипотезы. По мере накопления свидетельств МД и МНД происходит постепенное уточнение гипотезы (F’®В’) до 1.

В последующие годы было разработано множество экспертных систем различного назначения и на различных платформах. Например, экспертная система PROSPECT EXPLORER использует нечеткую логику рассуждений в помощь геологам для обнаружения горных аномалий и выделения минералов. Гибридная экспертная система FLEX нашла применение в различных финансовых системах. Она чередует прямой и обратный методы поиска решения при нечетких формулировках вопросов и правил. Экспертная система реального времени COMDALE/C предназначена для наблюдения и контроля над процессами в условиях производства. Она обрабатывает неопределенные знания и данные и позволяет вырабатывать реклмендации в непрерывном процессе принятия решения. Оболочка экспертной системы GURU нашла применение в различных сферах человеческой деятельности. В ней предлагается широкое многообразие инструментальных средств обработки информации, объединенных с возможностями нечеткого вывода от фактов к цели и от цели к фактам.

Вопросы и задачи

4.1.1. Написать формулы суждений:

а) “подготовка специалистов высокой квалификации возможна лишь на базе всемерного развития вузовской науки, усиления связи вузов­ской, академической и отраслевой науки, обеспечения единства науч­ной и учебной работы, широкого привлечения студентов к научным ис­следованиям";

b) "хлеба уцелеют в различных климатических и погодных усло -виях тогда и только тогда, когда будут выполнены все мелиоративные работы; если хлеба не уцелеют, то фермеры обанкротятся и оставят фермы; следовательно, необходимо выполнить все мелиоративные работы";

c) “если я поеду автобусом и автобус опоздает, то я опоздаю на работу; если я опоздаю на работу и стану огорчаться, то я не попадусь на глаза моему начальнику; если я не сделаю в срок важную работу, то я начну огорчаться и попадусь на глаза моему начальнику. Следовательно, если я поеду автобусом, а автобус опоздает, то я сделаю в срок важную работу”.

4.1.2. Доказать эквивалентность формул:

а) (AÚB)&(AÚùB)=A;

b) (AÚB)&(BÚC)&(CÚA)=(A&B)Ú(B&C)Ú(C&A);

c) (AÚB)&(AÚC)&(BÚD)&(CÚD)=((A&D)Ú(B&C)).

4.1.3. Привести формулу к виду ДНФ и КНФ:

а) (((A®B)®(C®ùA))®(ùB®ùC));

b) (((((A®B)®ùA)®ùB)®ùC)®C);

c) (A®(B®C))®(A®ùC)®(A®ùB).

4.1.4. Выполнить подстановку:

a) _Аò ^B&C(АÚB);

b) _(ùB®ùA ò ^(BÚC))_Аò ^(ùB®ùA) (A®BÚC);

c) _Аò^B (A®B) ® (ùB®ùA).

4.1.5. Доказать вывод по методу дедукции и принципу резолюции:

 

а) (AÚB); (A®C); (B®D)

(C Ú D);

b) (ùAÚB); (C®ùB)

(A® ù C);

c) ((AÚB)®(C&D)); ((DÚE)®F)

(A®F).

г) (AÚB); (A®B); (B®A)

(A&B).

4.2.1. Написать формулы суждений:

a) "все судьи - юристы, но не все юристы – судьи”;

b) “Судья, являющийся родственником потерпевшего, не может участвовать в рассмотрении дела. Судья X - родственник потерпевшего. Следовательно, судья X не может участвовать в рассмотрении дела”;

c) “К уголовной ответственности привлекаются лица, совершившие тайное похищение личного имущества граждан. Обвиняемый X не совершал тайного похищения личного имущества граждан. Следовательно, обвиняемый X не может быть привлечен к уголовной ответственности”;

d) “Если иск предъявлен недееспособным лицом, то суд оставляет иск без рассмотрения. Иск предъявлен недееспособным лицом. Следовательно, суд оставляет иск без рассмотрения”.

4.2.2. Привести формулу к виду ПНФ:

a) $x("y(P₁.(x; y)))&$x("y(P₂.(x; y)));

b) $x("y(P₁.(x; y)))Ú$x("y(P₂.(x; y)));

c) $x("y(P₁.(x; y))®$x("y(P₂.(x; y)));

d) "x("y(P₁.(x; y)))®$x($y(P₂.(x; y)));

e) "x(P₁.(x)Ú(P₂.(x))®"x(P₁.(x))Ú"y (P₂.(x));

4.3. Привести формулу к виду ССФ:

a) ($x"y(P₁.(x; y))&("x$y(P₂.(x; y)));

b) ($x"y$z"w(P(x; y; z; w));

c) $x(P₁(x))&$x(P₂.(x))®$x(P₁(x)&P₂.(x));

d) "y(P₁.(x))&"y (P₂.(x))®"y(P₁.(x)&(P₂.(x));

4.2.4. Доказать выводимость заключения методом дедукции и по принципу резолюции:

a) "x(P₁.(x)®ù P₂.(x)); "x(P₃.(x)®P₁.(x))

"x(P₃.(x)®ù P₂.(x));

b) "x(P₁.(x)®P₂.(x)& P₃.(x)); $x(P₁.(x)& P₄.(x))

$x(P₄.(x)&P₃.(x));

4.3.1. Выполнить операции над отношениями r₁, r₂, r₃, r₄. Написать формулы на языке реляционного исчисления с переменными-кортежами и на языке SQL.

a) union(r₁, r₂),

b) minus(r₃, r₄),

c) intersection(r₂, r₃),

d) join(r₁, r₄, r₁.A₄=r₄.A₄).

e) select(r₃, A₅>1),

f) select(join(r₁, r₄, r₁.A₄=r₄.A₄), A₂=c₃),

g) project(join(r₂, r₃, r₂.A₄>r₃.A₅), A₁,A₃,A₅),

h) product(r₂, r₄),

 

r1

A1

A2

A3

A4

A5

r2

A1

A2

A3

A4

A5

b1

c1

d1

b2

c3

d4

b2

c2

d2

b3

c3

d3

b3

c3

d3

b4

c4

d4

b4

c4

d4

b1

c2

d3

b1

c2

d3

b3

c2

d1

b2

c3

d4

b4

c3

d2

r3

A1

A2

A3

A4

A5

r4

A1

A2

A3

A4

A5

b4

c3

d2

b3

c2

d1

b3

c3

d3

b3

c3

d3

b1

c2

d3

b1

c2

d3

b1

c2

d3

b2

c2

d2

b4

c3

d2

b1

c1

d1

b2

c3

d4

b4

c3

d2

4.3.2. По таблицам “Расписание движения самолетов из Калининграда (аэропорт Храброво)” – РАСПИСАНИЕ_1 и “Расписание движения самолетов из Москвы (аэропорт Шереметьево)” - РАСПИСАНИЕ_2 ответить на вопросы:

а) Как организовать перелет Калининград–Москва–

С.-Петербург?

b) Как организовать перелет Калиниград-Москва-Красноярск?

c) Как организовать перелет Калининград-Москва-Киев?

d) Как организовать перелет Калининград-Москва-Новоси- бирск так, чтобы в четверг принять участие в работе конференции в10.00?

e) Как организовать перелет в среду Калининград-Москва-Красноярск?

f) Как организовать перелет Калининград-Москва-Тель-Авив?

g) На каких маршрутах вылетают самолеты из Калининграда после 18.00?

h) На каких маршрутах и когда вылетают самолеты из Калининграда по вторникам?

Для каждого вопроса написать формулы реляционной алгебры и реляционного исчисления с переменными-кортежами, написать программу на языке SQL, составить результирующие таблицы.

Примечание: резерв времени при переезде в Москве из одного аэропорта в другой не менее 3 часов;

 

РАСПИСАНИЕ_1

АЭРОПОРТ НАЗНАЧЕНИЯ	ОТПРАВЛЕНИЕ (ВРЕМЯ)
НОМЕР РЕЙСА	ДНИ ВЫЛЕТА	ВРЕМЯ (МЕСТНОЕ) ВЫЛЕТА	ВРЕМЯ ПРИЛЕТА
Москва ВН	К8986	1,2,3,4,5,6.7	08.15	11.05
Москва ВН		1,2,3,4,5,6,7	16.00	18.50
Москва ДМ	К8990	2,5	13.00	15.50
Новосибирск	К8351	5,6	19.00	05.30
Новосибирск	К8353		21.00	05.45
С-Петербург	К8485*	1,3,5	09.15	12.00
С-Петербугр	ПЛ8670		13.40	16.25
С-ПетербургГ	ПЛ8672		16.00	18.45
С-Петербург	ПЛ8668		19.05	21.50

 

РАСПИСАНИЕ_2

АЭРОПОРТ НАЗНАЧЕНИЯ	НОМЕР РЕЙСА	ДНИ ВЫЛЕТА	ВРЕМЯ ВЫЛЕТА	ВРЕМЯ (местное) ПРИЛЕТА
Киев	UN201	1,2,3,4,5	09.10	09.30
Киев	UN211	1,2,3,4,5	18.30	18.50
Красноярск1	UN5111	2,4,6	20.00	04.25
Красноярск1	UN5147	1,2,3,4,5,6,7	23.35	08.15
Новосибирск	UN107		21.50	05.55
Новосибирск	UN107		22.50	05.50
Санкт-Петербург**	UN121	1,2,3,4,5	07.50	09.00
Санкт-Петербург**	UN141	1,2,3,4,5	19.00	20.15
Тель-Авив	UN311	4,6,7	19.30	22.45

4.4.1 Пусть U = { u₁, u₂, u₃, u₄, u₅, u₆, u₇, u₈ } и даны нечеткие множества

A’={1/u₁, 0,1/u₂, 0,2/u₃, 0,3/u₄, 0,4/u₅} и

B’={0,1/u₁, 0,2/u₂, 0,3/u₆, 0,6/u₇, 0,8/u₈}.

Выполнить операции объединения, пересечения, дополнения, разности и симметрической разности над нечеткими множествами.

4.4.2. Выполнить алгебраические операции над нечеткими соответствиями h₁ и h₂, заданными таблицами:

 

	h1	y1	y2	y3	y4	y5				h2	y1	y2	y3	y4	y5
	x1	0,2	0,4	0,6	0,2	0,4				x1	0,4	0,2	0,8	0,2	0,4
	x2	0,3	0,5	0,7	0,5	0,3				x2	0,5	0,7	0,3	0,7	0,5
	x3	0,2	0,5	0,4	0,5	0,2				x3	0,5	0,2	0,6	0,2	0,5
	x4	0,3	0,6	0,9	0,6	0,3				x4	0,4	0,7	0,8	0,7	0,4

 

4.4.3. Найти композицию двух нечетких соответствий h₁ и h₂, заданных таблицами:

 

h1	y1	y2	y3		h2	z1	z2	z3	z4
x1	1,0	0,8	0,2		y1	0,3	0,3	0,3	0,2
x2	0,2	1,0	0,4		y2	0,2	0,2	0,4	0,3
x3	0,0	1,0	0,3		y3	0,1	0,3	0,2	0,6
x4	0,2	0,9	0,5
x5	0,3	0,7	1,0

 

4.4.4. Выполнить алгебраические операции над r₁ и r₂:

	r1	x1	x2	x3	x4	x5				r2	x1	x2	x3	x4	x5
	x1		0,3	0,2	0,1	0,4				x1		0,2	0,8	0,2	0,4
	x2	0,3		0,7	0,5	0,3				x2	0,5		0,8	0,7	0,2
	x3	0,2	0,5		0,5	0,2				x3	0,2	0,2		0,2	0,5
	x4	0,7	0,5	0,9		0,3				x4	0,4	0,7	0,8		0,4
	x5	0,6	0,7	0,2	0,3					x5	0,1	0,1	0,5	0,4

 

4.4.5. Найти степень достижимости вершин графа через промежуточные вершины согласно матрице нечеткой смежности:

r	x1	x2	x3	x4	x5
x1		0,2	0,4	0,6	0,8
x2	0,8		0,3	0,5	0,7
x3	0,6	0,7		0,4	0,6
x4	0,4	0,5	0,6		0,5
x5	0,2	0,3	0,4	0,5

⇐ Предыдущая20212223242526272829Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: