Метод критического пути в управлении

Проектом может быть названа разработка документации на автоматизированное рабочее место и ее внедрение в систему менеджмента на предприятии или подготовка архитектурной и проектно-сметной документации на строительство и выполнение строительно–монтажных работ при большом числе соисполнителей. Каждый проект имеет большой перечень работ с указанием их продолжительности и стоимости, последовательности и согласованности исполнения.

Тогда управление проектом в заданные сроки и при заданных ресурсах позволит:

· координировать исполнение работ всеми соисполнителями;

· предвидеть возможные задержки каждой работы и проекта в целом;

· устанавливать последовательность и сроки использования ограниченных ресурсов;

· анализировать компромиссные решения по затратам и срокам исполнения.

Для управления такими проектами были разработаны метод сетевого планирования и управления (СПУ) и метод критического пути (МКП).

Ориентированный граф является единственным средством для анализа проектов, требующих выполнения большого числа взаимосвязанных операций (работ). Такой граф имеет одну вершину-исток, которая представляет начало работ по всему проекту, и одну вершину-сток, которая представляет окончание всего проекта.

Между вершинами истоком и стоком есть множество вершин-событий, фиксирующих начало и/или окончание работы или комплекса работ t(i), а множество дуг, связывающих вершины-события, есть работы. Длина дуги-работы характеризует затраты временных или иных ресурсов t(i, j).Комплекс работ отображается на графе несколькими заходящими или исходящими дугами для одной вершины-события. Но это не мультиграф, т. к. каждая дуга имеет независимую вершину-исток или вершину-сток. В графе не должно быть петель и контуров. Если две или несколько работ должны начинаться одновременно, но привязаны к различным вершинам-истокам, то между этими вершинами должно быть отмечено ожидание. Чаще всего эти вершины соединяют пунктирной линией, отмечая как бы фиктивную работу.

Метод критического пути позволяет найти такую последователоьность работ от вершины-истока до вершины-стока, которая является минимальной среди всех максимальных по продолжительности или стоимости всех работ.

Рассмотрим фрагмент сети (см. рис. 3.32), включающий в себя пять вершин-событий и шесть дуг-работ: вершина-исток – x₀ – есть начало работ по проекту в момент времени t₀, вершина-сток - х_k – есть окончание работ по проекту в момент времени t_k, дуги-работы - t₀₁ и t₀₂ – имеют начало в момент t₀. Вершина-событие х₁ есть окончание одной работы t₀₁ в момент времени t₁=t₀+t₀₁ и формирует начало комплекса работ t₁₂ и t₁₃. Вершина-событие х₂ есть окончание работ t₀₂ и t₁₂ в моменты времени t₂’=t₀+t₀₂ и t₂”=t₁+t₁₂. Работа - t_2k не может начаться пока не будут окончены работы t₀₂ и t₁₂. Поэтому начало работы t_2k можно определить по значению t₂=max{t₂’, t₂”}.

При наличии нескольких дуг-работ, заходящих в вершину-событие следует определять для каждого события сети ранний момент его наступления t^p(x_i), как наиболее позднее окончание предшествующих работ, т. е. t^p(x_i)=max{(t^p(x_j)+t_i,j)}.

Вершина-событие х₃ есть окончание работы t₁₃ в момент времени t₃=t₁+t₁₃ и определяет возможность начать работы t_3k. Так как работы t_2k и t_3k должна начаться одновременно (см. пунктирную линию), то следует найти максимальное значение времени ожидания t_ожид.=max{t₂, t₃}.

Работы t_2k и t_3k обеспечивают завершение проекта к моменту времени t_k=max{t_ожид.+t_2k, t_ожид.+t_3k}.

Следовательно, наибольшая продолжительность работ по проекту есть максимальное значение t_k.

Расчет ранних моментов наступления каждого события следует начинать с x₀,

При наличии нескольких дуг-работ, исходящих из вершины-события следует определять для каждого события сети поздний момент его наступления t^п(x_i), как наименьшее раннее окончание последующих работ, т. е. t^п(x_i)=min{(t^п(x_j)-t_i,j)}.

Расчет поздних моментов наступления каждого события следует начинать с x_k.

Для событий, связанных с ожиданием ранний и поздний моменты времени расчитываются по формулам:

t^p_ожид^.(х_i;х_j)=max{t^p(х_i); t^p(х_j)}, tⁿ_ожид^.(х_i;х_j)=min{tⁿ(х_i); tⁿ(х_j)}.

Максимально время, на которое можно задержать наступление некоторого события без задержки срока завершения всего проекта, называют резервом времени события, т. е. t⁰(х_i)=(tⁿ(х_i)-t^p(х_i)).

Максимально время, на которое можно продлить исполнение работы без задержки срока завершения всего проекта, называют резервом времени на работу, т. е. t⁰_i,j=(tⁿ(х_j)- t^p(х_i)-t_i,j).

Критический путь сетевой модели представляет последовательность работ и событий, имеющих нулевой резерв времени на события и работы, т. е.

t⁰(x_i)=0,

t⁰_i,j=(tⁿ(х_j)-t^p(х_i)-t_i,j)=0.

Для компактного графического изображения всех показателей каждого события каждую вершину-событие представим в виде круга, разбитого на четыре сектора. В каждом секторе указаны четыре показателя: индекс вершины (i), ранний момент события t^p(x_i), поздний момент события tⁿ(x_i) и резерв времени на событие t⁰(x_i). Дуги графа изображают работы, а пунктирная линия – фиктивную работу - ожидание.

Для иллюстрации возможностей сетевого управления работами по проекту рассмотрим сетевую модель (см. рис. 3.33).

Алгоритм расчета раннего момента наступления событий:

шаг 1: принять для начальной вершины графа t^p(0)=0 и p=0, где p-шаг итерации;

pi	i	j=hi	tp(j)={(tp(i)+t(i, j))}	tp(j)=maxi{(tp(i)+t(i, j))}
			tp(1)=tp(0)+t(0, 1)=3	tp(1)=3
			tp(2)=tp(0)+t(0, 2)=2
			tp(2)=tp(1)+t(0, 2)=8	tp(2)=8
			tp(3)=tp(1)+t(1, 3)=5	tp(3)=5
			tp(5)=tp(1)+t(1, 5)=10
			tp(4)=tp(2)+t(2, 4)=18
			tp(5)=tp(3)+t(3, 5)=13	tp(4)=tp(5)=18
			tp(6)=tp(4)+t(4, 6)=20
			tp(7)=tp(4)+t(4, 7)=22	tp(7)=22
			tp(6)=tp(5)+t(4, 6)=22	tp(6)=22
		k	tp(k)=tp(5)+t(5, k)=24
		k	tp(k)=tp(6)+t(6, k)=27
		k	tp(k)=tp(7)+t(7, k)=23	tp(k)=27

шаг 2: определить на шаге итерации p ранний момент наступления события j по формуле: t^p(j)=(t^p(i)+t(j, i)), где t^p(i) - события i с известным ранним моментом наступления; t(j, i) –продолжи- тельность работы t(i, j) от события, имеющего t^p(i);

а) если к вершине j подходит одна дуга (i, j), то принять t^p(j)=(t^p(i)+t(j, i)),

б) если к вершине j подходит несколько дуг {(i, j)}, то сравнить и найти максимальное значение раннего момента наступления события j по формуле: t^p(j)=max_i{(t^p(i)+t(i, j))}.

шаг 3: если p=(n-1), то конец, иначе принять p=(p+1) и перейти к шагу 2 алгоритма.

Результаты вычислений представлены таблицей.

Алгоритм расчета позднего момента наступления события:

шаг 1: принять для конечной вершины графа tⁿ(k)=t^p(k) и р=0, где р-шаг итерации;

шаг 2: определить на шаге итерации р поздний момент наступления события j по формуле: tⁿ(j)=(tⁿ(i)-t(j, i)), где tⁿ(i)-событие i с известным поздним моментом наступления; t(j, i) –продолжитель- ность работы (i, j) от события, имеющего tⁿ(i);

а) если от вершины j отходит одна дуга (i, j), то принять tⁿ(j)=(tⁿ(i)-t(j, i);

б) если от вершины j отходит несколько дуг (i, j), то сравнить и найти минимальное значение позднего момента наступления события j по формуле: tⁿ(j)=min_i{(tⁿ(i)-t(j, i))};

шаг 3: если р=(n-1), то конец, иначе принять р=(р+1) и перейти к шагу 2 алгоритма.

Результаты вычисления представлены таблицей.

pi	i	j=hi-1	tn(j)=(tn(i)-t(j, i))	tn(j)=mini{(tn(i)-t(j, i))}
	k		tn(7)=(tn(k)-t(k, 7))=26	tn(7)=26
			tn(6)=(tn(k)-t(k, 6))=22	tn(6)=22
			tn(5)=(tn(k)-t(k, 5))=21
			tn(4)=(tn(7)-t(4, 7))=22
			tn(5)=(tn(6)-t(5, 6))=18
			tn(4)=(tn(6)-t(4, 6))=20	tn(5)=tn(4)=18
			tn(3)=(tn(5)-t(3, 5))=10	tn(3)=10
			tn(1)=(tn(5)-t(1, 5))=11
			tn(2)=(tn(4)-t(2, 4))=8	tn(2)=8
			tn(1)=(tn(3)-t(1, 3))=8
			tn(1)=(tn(2)-t(1, 2))=3	tn(1)=3
			tn(0)=(tn(2)-t(0, 2))=6
			tn(0)=(tn(1)-t(0, 1))=0	tn(0)=0

Алгоритм расчета резерва времени события:

шаг 1: принять р=0, где р-шаг итерации;

шаг 2: определить на шаге итерации р индекс события i и резерв его ожидания по формуле: t⁰(i)=(tⁿ(i)-t^p(i));

шаг 3: если р=(n-1), то конец, иначе принять р=(р+1) и перейти к шагу 2.

pi
i									k
t0(i)

Результаты вычислений представлены таблицей.

Алгоритм расчета резерва временина работу:

шаг 1: принять р=0 и выделить любую дугу (i,j);

шаг 2: определить резерв времени для работы (i,j) по формуле t_i,j^0.=(tⁿ(j)- t^p(i)-t_j,i);

шаг 3: если р=m, где m-число дуг, то конец, иначе р=(р+1), выделить новую дугу (i,j) и перейти к шагу 2 алгоритма.

Результаты расчетов приведены в таблице.

pi	(i,j)	ti,j0		pi	(i,j)	ti,j0
	(0, 1)				(3, 5)
	(0, 2)				(4, 6)
	(1, 2)				(4, 7)
	(1, 3)				(5, 6)
	(1, 5)				(5, k)
	(2, 4)				(6, k)
					(7, k)

 

Произведенный анализ показывает, что

· события 1, 2, 4, 5, 6, имеют резерв времени равный нулю; cледовательно, они принадлежат критическому пути;

· работы (0, 1); (1, 2); (2, 4); (5, 6); (6, k) имеют резерв времени равный нулю; cледовательно, они также принадлежат критическому пути;

· события 3 и 7 имеют резерв времени, что позволяет ослабить внимание на исполнение работ t₁₃, t₃₅, t₄₇, t_7k или уменьшить затраты на исполнение этих работ, но не более указанных резервов;

· работы (0;2); (1;5); (4;6); (5;k) имеют резерв времени, что позволяет продлить исполнение этих работ или уменьшить затраты ресурсов, но не более указанных резервов.

Выполненные расчеты представлены на рис. 3.33. Там же показан полужирной линией критический путь, соединяющий события, имеющие нулевой резерв времени, дугами-работами, также имеющими нулевой резерв времени.

Нечеткие графы

Во многих практических задачах невозможно установить четкую принадлежность вершин графу и/или четкие отношения между его вершинами. В этом случае говорят о нечетких графах.

Графы могут быть нечетко ориентированными и нечетко неориентированными.

Нечетко ориентированные графы представляют модели систем, в которых существенным является неправление нечетких связей между элементами. К таким системам относятся нечеткие алгоритмы задач организационно-экономического управления, нечеткие системы каталогов и/или баз данных и т. п.

Нечетко неориентированные графы представляют модели систем, в которых неправление нечетких связей между элементами является несущественным.

Нечеткие графы могут быть заданы в двух формах:

а) G’=<X, r’>, где r’={m(x, x_i)/(x, x_i)| x, x_iÎX} есть нечеткое отношение между вершинами графа,

 

б) G’=<X, h’>, где h’(x)={m(x_j)/x_i | x, x_j ÎX} есть нечеткое отображение множествa вершин графа.

Вершины x и x_i графа G’ называют нечетко смежными, если для r’ имеем 0<m(x, x_i)<1, а для h’(x) имеем 0<m(x_i)<1. Чаще всего рассматривают нечеткую смежность вершин графа при 0,5£m(x, x_i) или 0,5<m(x_i).

Вершину x и дугу (x, x_i) называют нечетко инцидентными, если m(x, x_i) интерпретируется как степень инцидентности.

Матрица смежности нечеткого графа есть квадратная таблица ||r_{i j}||, строки и столбцы которой помечены вершинами графа, а в позициях матрицы указаны значения m(x_i, x_j).

Матрица инциденции нечеткого графа есть прямоугольная таблица, строки которой помечены ребрами для неориентированного графа или дугами для ориентированного, а столбцы вершинами графа. Каждая вершина графа xÎX характеризуется степенью или валентностью s_i, равной числу ребер или дуг, инцидентных данной вершине и имеющих m(x_i)>0. Для ориентированного графа определяют полустепени исхода - s⁺_i и захода -s^-_i. Каждой вершине графа приписывают максимальную степень инциденции m(x_i).

Подробное описание нечетких отображений и отношений рассмотрено в 1.3.2, а описание алгебраических операций и преобразований в 1.7.

Пример: пусть дан неориентированный граф G’=<X, r’>, где X={x₁, x₂, x₃, x₄, x₅}.

Множество нечетких отношений и отображений заданы списками: r={0,7/(x₁, x₂), 0,2/(x₁, x₄), 0,1/(x₁, x₅), 0,8/(x₂, x₂), 0,4/(x₂, x₄), 0,8/(x₂, x₅), 0,9/(x₃, x₄), 0,3/(x₃, x₅), 0,2/(x₄, x₄)} и

xi	h’xi
x1	0,7/x2, 0,2/x4, 0,1/x5
x2	0,7/x1, 0,8/x2, 0,4/x4, 0,8/x5
x3	0,9/x4, 0,3/x5
x4	0,2/x1, 0,4/x2, 0,9/x3, 0,2/x4
x5	0,1/x1, 0,8/x2, 0,3/x3

 

Иногда в нечетком графе между какими-то парами вершин есть несколько дуг или ребер. Такие графы называют нечеткими мультиграфами. Каждое ребро или дуга могут иметь различные степени инциденции с инцидентными им парами вершин m(x_i, x_j). Поэтому каждая из них участвует в анализе нечеткого графа отдельно.

Данные нечетких отношений и отбражений примера удобно представить матрицами смежности и/или инциденции, что позволит применить матричные методы в исполнении алгебраических операций.

r’	x1	x2	x3	x4	x5	s+i	m(xi)		h’	x1	x2	x3	x4	x5
x1		0,7		0,2	0,1		0,8		(x1, x2)	0,7	0,7
x2	0,7	0,8		0,4	0,8		0,8		(x1, x4)	0,2			0,2
x3				0,9	0,3		0,9		(x1, x5)	0,1				0,1
x4	0,2	0,4	0,9	0,2			0,9		(x2, x2)		0,8
x5	0,1	0,8	0,3				0,8		(x2, x5)		0,8			0,8
s-i	0,7	0,8	0,9	0,9	0,8				(x3, x4)			0,9	0,9
									(x3, x5)			0,3		0,3
									(x4, x4)				0,2
									s-i	0,7	0,8	0,9	0,9	0,8

Вопросы и задачи

3.1 Граф задан списком отношений:

ri	r1	r2	r3	r4	r5	r6
(xi; xj)	(x1; x3)	(x2; x4)	(x2; x5)	(x3; x4)	)x3; x5)	(x4; x5)

а) нарисуйте граф;

b) укажите разрез для X¢={x₁, x₂, x₄} и X\X¢={x₃, x₅, x₆};

c) нарисуйте частичный граф на рёбрах {r₂, r₄, r₆};

d) нарисуйте суграф на рёбрах {r₁, r₃, r₅, r₇};

e) нарисуйте подграф на вершинах x₂,x₄,x₅,x₆;

f) составьте матрицу инциденции и матрицу смежности.

 

3. 2 Граф задан списком отображений:

xi	x1	x2	x3	x4	x5	x6
hXi	x2	x1, x4	x4	x2, x3, x5, x6	x4	x4

а) нарисуйте граф;

b) укажите маршрут и переход из вершины x₃ в вершину x₆;

с) укажите разрез для X¢={x₁, x₂, x₄} и X\X¢={x₃, x₅, x₆};

d) cоставьте матрицу инциденции и матрицу смежности.

 

3.3 Реберно-взвешенный граф задан списком отношений:

ri	r1	r2	r3	r4	r5	r6
(xi; xj)	(x1; x3)	(x2; x4)	(x2; x5)	(x3; x4)	)x3; x5)	(x4; x5)
li

а) нарисуйте граф;

b) составьте матрицу весов.

 

3. 4. Найти число компонент связности графа

 

3.5. Найти цикломатические и хроматические числа, числа внутренней и внешней устойчивости для графов. Изоморфны ли графы?

 

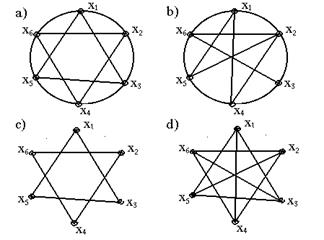3.6. Для четырех графов найти: дополнение, объединение графов a) и d), пересечение графов b) и d), композицию графов c) и d).

3. 7. Найти основные числа графа (n, m, k, d, l, g, r, e, j, f).

 

 

3.8. Найти кратчайшие пути между любой парой вершин.

 

3.9 Найти распределение максимального потока в сети. Вершина x₁ – исток, вершина x₉ – сток. На каждой дуге указано:

[величина потока - j(i, j), пропускная способность – C(i,j)].

3.10 Найти критический путь по алгоритму управления проектом (СПУ),. Продолжительности работ (длина дуги) приведены на рисунке.

 

 

 

 

⇐ Предыдущая12131415161718192021Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: