 |
Глава 6. Конечные автоматы
|
|
|
|
Теория автоматов наиболее тесно связана с теорией алгоритмов. Это объясняется тем, что автомат преобразует дискретную информацию по шагам в дискретные моменты времени и формирует результирующую информацию по шагам заданного алгоритма. Эти преобразования возможны с помощью технических и/или программных средств.
Единый подход в описании технических и программных средств определил понятие " автомат ", как математическую модель системы, обеспечивающей прием, хранение и обработку информации. Ограничение числа параметров математической модели определило другое понятие – “ конечный автомат”.
При анализе автоматов изучают их поведение при различных возмущающих воздействиях и минимизируют число состояний автомата для работы по заданному алгоритму. Такой автомат называют абстрактным.
При синтезе автоматов формируют систему из элементарных автоматов, эквивалентную заданному абстрактному автомату. Такой автомат называют структурным.
Абстрактный автомат
Абстрактным автоматом называют математическую модель дискретного устройства, имеющего один входной канал, куда поступают последовательности символов какого-то языка, один выходной канал, с которого снимают последовательности символов, возможно, другого языка и находящегося в каждый из моментов дискретного времени в каком-либо состоянии.

Слова входного языка можно представить символами множества X={x1,x2,...xn}, который называют входным алфавитом, а слова выходного языка - символами множества Y={y1,y2,...yp}, который называют выходным алфавитом.
Множество состояний автомата Q={q1,q2,...qm} называют алфавитом состояний. Понятие "состояние" автомата используют для того, чтобы установить функциональную зависимость генерируемых автоматом символов от символов входного языка при реализации автоматом заданного алгоритма. Для каждого состояния автомата qÎQ и для каждого символа входного языка xÎX в момент дискретного времени [t] на выходе устройства генерируется символ yÎY. Эту зависимость определяет функция выходов автомата - j. Для каждого текущего состояния автомата qÎQ и для каждого символа xÎX в момент дискретного времени [t] автомат переходит в очередное состояние qÎQ. Эту зависимость определяет функция переходов автомата - y.
|
|
|
Функционирование автомата есть последовательность состояний автомата (q1[[1]q2[2]q3[3]...) и выходных символов (y1[1]y2[2]y3[3]...) под влиянием последовательности символов на входе автомата (x1[1]x2[2]x3[3]...). Каждый символ входной последовательности считывается в дискретный моменты времени [t]=1, 2, 3,...Поэтому в прямых скобках. указывают моменты дискретного времени, которые называют тактами,
Математическая модель конечного автомата есть
M =<X; Y; Q; j; y>
| где X={ x1, x2,...xn } | - | - множество символов входного алфавита; |
| Y={ y1, y2,..yp } | - | - множество символов выходного алфавита; |
| Q={q1, q2,...qm} | - | - множество символов состояний автомата; |
| y: (QÄX) ®Q | - | - функция переходов автомата для отображения пары (q; x) текущего момента времени [t] в состояние q очередного момента времени [t+1]; |
| j: (QÄX) ®Y | - | - функция выходов автомата для отображения пары (q; x) текущего момента времени [t] в символ y выходного канала этого же момента времени [t]. |
Так как области определения функций переходов и выходов совпадают, то обобщенный оператор поведения автомата можно описать так:
<y, j>: (QÄX) ®(QÄY).
Функционирование автомата в дискретные моменты времени может быть описано системой рекуррентных соотношений:
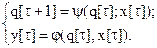
Если на входе автомата слово a = (x1x2x3...xt), то, считывая последовательно символы этого слова, на выходе автомата генерируется последовательность символов слова b по схеме:
|
|
|
b[1]=(j(q[1]; x1[1]));
b[2]=(j(q[1]; x1[1]) j(q[2]; x2[2])) = (j(q[1]; x1[1])j(q[1]; (x1[1]x2[2])));
……………………………………………..............................................
b[t]=(j(q[1];x1[1])j(q[2];x2[2])...j(q[s];xt[t])) =
= (j(q[1];x1[1])j(q[1];(x1[1]x2[2]))...j(q[1];(x1[1]x2[2]... xt[t])));
Так как на каждом i-ом такте к слову длины (i-1) приписывается справа очередной символ j(q[1]; (x1[1]x2[2]...xi[i])), то последовательность символов выходного слова можно записать так:
b= (j(q;x1)j(q;(x1x2))...j(q;(x1x2...xs)))=(j(q; a)).
Если считывание символов входного слова a выполняется последовательно слева направо, то всегда найдется такая последовательность (x1x2...xs-1)=g, для которой a = ((x1x2...xs-1)xs) =(gxs), где g =(x1x2...xs-1) –"голова" слова a, а xs –“хвост" слова a.
Поэтому если входное слово a = (gxs), то выходное слово b можно записать так
b=j(q; a) = j(y(q;g);xs
Это означает, что последний символ слова b есть результат работы автомата, начавшего работу в состоянии q и считавшего последний символ слова a, но значение этого символа зависит от всей входной последовательности g.
Длина выходного слова всегда равна длине входного слова.
Изменение состояний автомата для последовательности символов слова a = (x1x2x3...xs) может быть описано следующей схемой:
q[2] = y(q[1];x1[1]);
q[3] = y(q[2];x2[2]) = y(y(q[1];(x1[1]);x2[2]));
............................................................................................
q[t+1] =y(q[s];xt[t])=y(y..(y (y (q[1];x1[1]);x2[2]);..xt-1[t-1]);xt [t]),
где q[1] - начальное состояние автомата.
Так как за один такт автомат считывает один символ входного слова, то в последовательности состояний автомата можно не указывать номер такта, т. е. описывать так:
q[t+1] = y(y... (y(y(y(q;x1);x2);x3)...xt-1);xt).
Если входное слово a =(gxt), то изменение состояния автомата может быть описано так:
q[t+1] = y(y(q, g);xt).
Это означает, что q[t+1] есть последнее состояние автомата, начавшего работу в состоянии q и считавшего последний символ слова a в момент дискретного времени t.

Если функции переходов и выходов однозначно определены для каждой пары (q; x)Î(QÄX), то автомат называют детерминированным. В противном случае автомат называют недетерминированным или частично определенным.
Если функция переходов и/или функция выходов являются случайными, то автомат называют вероятностным.
Если у автомата задано начальное состояние q=q0ÎQ, в котором он находится всегда до приема первого символа входного слова, то автомат называют инициальным.
|
|
|
В этом случае модель автомата записывают так:
M=<X; Y; Q; j; y;q0>.
Последовательность символов в слове b и последовательность состояний автомата q однозначно определяются начальным состоянием автомата q=q0 и последовательностью символов во входном слове a.
Отображение входного слова a на выходное слово b называют автоматным отображением, то есть b=М(q0; a), а М называют автоматным оператором.
Автоматное отображение обладает свойствами:
· входное и выходное слова имеют одинаковую длину;
· yi-ый символ выходного слова зависит от всей последовательности символов входного слова, до xi-го включительно.
Типы конечных автоматов
По способу формирования функций выхода выделяют автоматы Мили и Мура.
В автомате Мили функция выходов j определяет значение выходного символа по классической схеме абстрактного автомата. Математическая модель, схема рекуррентных соотношений и функциональная схема автомата Мили не отличаются от одноименных модели, соотношений и схемы абстрактного автомата, т.е.


В автомате Мура функция j определяет значение выходного символа только по одному аргументу - состоянию автомата. Символ y[t] в выходном канале существует пока автомат находится в состоянии q[t].
Математическая модель, схема рекуррентных соотношений и функциональная схема автомата Мура имеют вид:


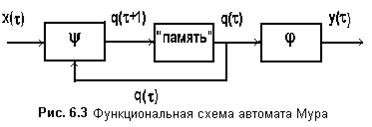
Объединение автоматов Мили и Мура представляет С-автомат:


Математические модели, опирающиеся только на два носителя алгебры, представляют особые классы автоматов.
Если X=Æ, то математическая модель и система рекуррентных соотношений абстрактного автомата имеют вид:



Особенностью такого автомата является генерация последовательности символов выходного слова только в зависимости от одного аргумента - состояний автомата. Такие автоматы называют порождающими или автономными. С помощью такого автомата генерируется последовательность управляющих команд.
|
|
|
Если Y=Æ, то математическая модель и система рекуррентных соотношений имеют вид:

q[t+1] =y(q[t];x[t]);

Особенностью такого автомата является распознавание в последовательности изменений аргументов функции переходов
(qi[t]; xi[t]) и перевод автомата в заключительное состояние qk.
С помощью такого автомата обнаруживают возмущения со стороны внешней среды или распознают последовательность входных символов. Поэтому такие автоматы называют распознающими.
Если Q=Æ, то математическая модель и система рекуррентных соотношений имеют вид:

y[t] = j(x[t]).

Особенностью функционирования такого автомата является отсутствие "памяти", т.е. на каждый символ входного алфавита автомат генерирует символ выходного алфавита без учета состояния автомата. Такие автоматы чаще всего называют комбинационными автоматами.
Описание автоматов
Автоматы удобно описывать таблицами, отражающими функции:
y: (QÄX)®Q (см. таблицу 6.1),
j: (QÄX)®Y (см. таблицу 6.2).
. таблица 6.1 таблица 6.2
| Детерминированный автомат y: (QÄX)®Q | Детерминированный автомат j: (QÄX)®Y | ||||||||||||
| qiÎQ | xiÎX | qiÎQ | xiÎX | ||||||||||
| x1 | x2 | … | xn | x1 | x2 | … | xn | ||||||
| q1 | q | q | q1 | y | y | … | y | ||||||
| q2 | q | q | q2 | y | y | … | y | ||||||
| … | … | … | … | … | … | … | … | ||||||
| qm | q | q | … | q | qm | y | y | … | y | ||||
Обычно эти таблицы совмещают в одну, которая раскрывает оператор поведения <y; j>: (QÄX)®(QÄY). В позициях таблицы 6.3 записывают пары (q[t+1]; y[t]) для автомата Мили, а позициях таблицы 6.4 только символы состояния.для каждого входного символа
| Таблица 6.3. | Таблица 6.4. | |||||||||||
| Детерминированный автомат <j, y>:(QÄX)®(QÄY) | Детерминированный автомат y: (QÄX)®Q | |||||||||||
| qÎQ | xiÎX | qÎQ | xiÎX | yÎY | ||||||||
| x1 | x2 | … | xn | x1 | x2 | … | xn | |||||
| q1 | q; y | q; y | … | q; y | q1 | q | q | … | q | y1 | ||
| q2 | q; y | q; y | … | q; y | q2 | q | q | … | q | y2 | ||
| … | … | … | … | … | … | … | … | … | … | … | ||
| qm | q; y | q; y | … | q; y | qm | q | q | … | q | ym | ||
Таблицы абстрактного автомата совпадают с таблицами автомата Мили. Поэтому таблица 6.3 описывает поведение автомата Мили. Таблица автомата Мура (см. таблицу 6.4) несколько отличается от таблицы автомата Мили, так как j: Q®Y. Значение выходного символа приписывают, как метку, состоянию автомата.
Описание С-автомата есть объединение таблиц 6.3 и 6.4. Так как в таблицах 6.3 и 6.4 определены все позиции, то такими таблицами дано описание детерминированных автоматов.
В практике часто функции переходов и/или выходов не определены для некоторых символов входного алфавита. В этом случае говорят, что автомат недетерминированный или частично определенный. При описании таких автоматов неопределенные позиции таблиц помечаются символом "*". Например, в таблицах 6.5, 6.6, 6.7 и 6.8 приведено описание недетерминированных автоматов.
|
|
|
| Таблица 6.5. | Таблица 6.6. | |||||||||||||
| Недетерминированный автомат y: (QÄX)®Q | Недетерминированный автомат j: (QÄX)®Y | |||||||||||||
| qiÎQ | xiÎX | qiÎQ | xiÎX | |||||||||||
| x1 | x2 | … | xn | x1 | x2 | … | xn | |||||||
| q1 | q | * | … | q | q1 | y | * | … | y | |||||
| q2 | q | q | … | * | q2 | * | y | … | y | |||||
| … | … | … | … | … | … | … | … | … | … | |||||
| qm | * | q | … | q | qm | * | y | … | * | |||||
| Таблица 6.7. | Таблица 6.8. | ||||||||||||||
| Недетерминированный автомат Мили <y, j>: (QÄX) ®(QÄY) | Недетерминированный автомат Мура y: (QÄX)®Q; j: Q®Y | ||||||||||||||
| qiÎQ | x iÎX | qiÎQ | x iÎX | yiÎY | |||||||||||
| x1 | x2 | … | xn | x1 | x2 | … | xn | ||||||||
| q1 | q; y | *; * | … | q; y | q1 | q | * | … | q | y1 | |||||
| q2 | q; * | q; y | … | *; y | q2 | q | q | … | * | * | |||||
| … | … | … | … | … | … | … | … | … | … | … | |||||
| qm | *; * | q; y | … | q; * | qm | * | q | … | q | ym | |||||
Поведение автомата удобно анализировать с помощью графов, вершинами которого являются элементы множества qÎQ. Тогда любая вершина-исток есть образ текущего состояния q[t], а любая вершина-сток - образ очередного состояния q[t+1]. Дуги отображают переход автомата из одного состояния в другое (q[t];q[t+1]) под воздействием x[t]ÎX. Для описания автомата с помощью графов удобно воспользоваться таблицами соединений состояний автомата. Строки и столбцы такой таблицы представляют символы qÎQ. Следовательно, число строк и столбцов таблицы равно m. Строки этой таблицы характеризуют текущее состояние, т.е. q[t], а столбцы - очередное, т.е. q[t+1].
Позиции таблицы заполняют значениями пары (x[t]/y[t]) для соответствующего перехода автомата из текущего состояния в очередное.
Таблицей 6.9 дано описание соединений состояний автомата Мили, а таблицей 6.10 - автомата Мура. Для автомата Мили на дугах графа указывают пару (входной символ / выходной символ). Для автомата Мура - только входной символ, так как выходной символ y, приписывают к вершине графа.
| Таблица 6.9. | Таблица 6.10. | ||||||||||||
| Соединение состояний автомата Мили <y; j>: (QÄX) ®QÄY) | Соединение состояний автомата Мура y: (QÄX) ® Q; j: Q®Y | ||||||||||||
| qÎQ | очередное состояние qÎQ | qÎQ | очередное qÎQ | выход yÎY | |||||||||
| q1 | q2 | … | qm | q1 | q2 | … | qm | ||||||
| q1 | x/y | x/y | … | x/y | q1 | x | x | … | x | y1 | |||
| q2 | x/y | x/y | … | x/y | q2 | x | x | … | x | y2 | |||
| … | … | … | … | … | … | … | … | … | … | … | |||
| qm | x/y | x/y | … | x/y | qm | x | x | … | x | ym | |||
При начертании графа детерминированного автомата следует соблюдать следующие условия:
· для каждого символа xÎX есть дуга, исходящая из qÎQ;
· каждый символ xÎX у каждой вершины-истока принадлежит только одной дуге;
· если между двумя вершинами существует несколько дуг, что возможно при различных символах на входе, то есть xi ¹xj, то эти дуги могут быть заменены одной дугой с указанием дизъюнктивной связи этих переходов (например, если yu¹yv, то на дуге следует указать (xi /yuÚxj /yv);.если yu=yv=y, то - (xiÚxj) /y).
Пример: дана таблица поведения детерминированного автомата Мили.
Составить таблицу соединения состояний автомата и начертить граф. Найти генерируемые автоматом слова b для различных начальных состояний, если на входе автомата задано слово a=(x1x2x3x4x4x3x2x1).
| <y, j>: (QÄX) ®(QÄY) | ||||
| qÎQ | xÎX | |||
| x1 | x2 | x3 | x4 | |
| q1 | q2; y1 | q3; y1 | q4; y1 | q1; y3 |
| q2 | q3; y3 | q4; y1 | q1; y2 | q2; y2 |
| q3 | q2; y1 | q3; y2 | q1; y1 | q2; y3 |
| q4 | q4; y2 | q1; y1 | q2; y2 | q1; y1 |
| Таблица соединений автомата Мили | ||||
| qÎQ | очередное состояние qÎQ | |||
| q1 | q2 | q3 | q4 | |
| q1 | x4/ y3 | x1/ y1 | x2/ y1 | x3/ y1 |
| q2 | x3/ y2 | x4/ y2 | x1/ y3 | x2/ y1 |
| q3 | x3/y1 | (x1/y1)Ú(x4/y3) | x2/y2 | — |
| q4 | (x2Úx4)/y1 | x3/y2 | — | x1/y2 |
В позициях таблицы значения (x/y), соответствуют переходу из состояния q[t] в состояние q[t+1].

Граф детерминированного автомата Мили.
Следует обратить внимание, что переход из состояния q3 в q2 обусловлен двумя входными символами x1 и x4, а для каждой пары (q3; x1) и (q3; x4) автомат генерирует в выходном канале соответствующий символ y1 или y3. Поэтому на дуге (q3; q2) следует указать (x1/y1Úx4/y3). Переход из состояния q4 в q1 обусловлен также двумя входными символами x2 и x4, но автомат генерирует только один символ y1. Поэтому на дуге (q4;q1) следует указать (x2Úx4) /y1.
Для поиска слов b при различных начальных условиях необходимо проследить всю последовательность изменения состояний автомата:
пусть q1=q0, тогда
a[t]: x1[1] x2[2] x3[3] x4[4] x4[5] x3[6] x2[7] x1[8]
q[t+1]: q1[1] q2[2] q4[3] q2[4] q2[5] q2[6] q1[7] q3[8] q2[9]
b[t]: y1[1] y1[2] y2[3] y2[4] y2[5] y2[6] y1[7] y1[8],
то есть b=(y1y1y2y2y2y2y1y1);
пусть q2=q0, тогда
a[t]: x1[1] x2[2] x3[3] x4[4] x4[5] x3[6] x2[7] x1[8]
q[t+1]: q2[1] q3[2] q3[3] q1[4] q1[5] q1[6] q4[7] q1[8] q2[9]
b[t]: y3[1] y2[2] y1[3] y3[4] y3[5] y1[6] y1[7] y1[8],
то есть b=(y3y2y1y3y3y1y1y1);
Таким образом при различных начальных состояниях реакция автомата на одинаковые слова различна. Это подтверждает необходимость указания начального состояния qi=q0.
Пример: дана таблица поведения детерминированного автомата Мура. Составить таблицу соединения состояний автомата и начертить граф. Найти генерируемые автоматом слова b для различных начальных состояний, если на входе автомата задано слово a=(x1x2x3x4x4x3x2x1).
| y: (QÄX)®Q; jQ®Y | ||||||||||||||
| qÎQ | xÎX | выход yÎY | ||||||||||||
| x1 | x2 | x3 | x4 | |||||||||||
| q1 | q2 | q3 | q4 | q1 | y1 | |||||||||
| q2 | q3 | q4 | q1 | q2 | y3 | |||||||||
| q3 | q2 | q3 | q1 | q2 | y2 | |||||||||
| q4 | q4 | q1 | q2 | q1 | y1 | |||||||||
Переход из состояния q3 в q2 обусловлен двумя входными символами x1 и x4. Поэтому на дуге (q3;q2) указать (x1Úx4). Переход из состояния q4 в q1 также обусловлен двумя символами x2 и x4. Поэтому на дуге (q4;q1) указать (x2Úx4).
Таблица соединений автомата Мура
| qÎQ | очередное состояние qÎQ | выход yÎY | |||
| q1 | q2 | q3 | q4 | ||
| q1 | x4 | x1 | x2 | x3 | y1 |
| q2 | x3 | x4 | x1 | x2 | y3 |
| q3 | x3 | (x1Úx4) | x2 | — | y2 |
| q4 | (x2Úx4) | x3 | — | x1 | y1 |
Для поиска слов b при различных начальных условиях необходимо проследить всю последовательность изменения состояний автомата для каждого очередного символа слова a:
пусть q1=q0, тогда
a[t]: x1[1] x2[2] x3[3] x4[4] x4[5] x3[6] x2[7] x1[8]
q[t+1]: q1[1] q2[2] q4[3] q2[4] q2[5] q2[6] q1[7] q3[8] q2[9]
b[t]: y1[1] y3[2] y1[3] y3[4] y3[5] y3[6] y1[7] y2[8],
то есть b=(y1y3y1y3y3y3y1y2);
пусть q2=q0, тогда
a[t]: x1[1] x2[2] x3[3] x4[4] x4[5] x3[6] x2[7] x1[8]
q[t+1]: q2[1] q3[2] q3[3] q1[4] q1[5] q1[6] q4[7] q1[8] q2[9]
b[t]: y3[1] y2[2] y2[3] y1[4] y1[5] y1[6] y1[7] y1[8],
то есть b=(y3y2y2y1y1y1y1y1).
Этот пример также подтверждает необходимость указания начального состояния q=q0.

Граф детерминированного автомата Мура.
Пример: дана таблица поведения недетерминированного автомата Мили. Составить таблицу соединений автомата и начертить граф. Найти генерируемые автоматом слова b для различных начальных состояний.
| <y, j>: (QÄX) ®(QÄY) | |||||
| qÎQ | xÎX | ||||
| x1 | x2 | x3 | x4 | ||
| q1 | q2; y1 | q3; * | q4; y1 | q1; y3 | |
| q2 | *; y3 | q4; y1 | q1; y2 | q2; * | |
| q3 | q2; y1 | *; * | q1; y1 | q2; y3 | |
| q4 | q4; y2 | q1; y1 | q2; y2 | *; y1 | |
Таблица cоединений недетерминированного автомата Мили
| qÎQ | очередное состояние qÎQ | |||
| q1 | q2 | q3 | q4 | |
| q1 | x4/y3 | x1/y1 | x2/* | x3/y1 |
| q2 | x3/y2 | x4/* | — | x2/y1 |
| q3 | x3/y1 | (x1/y1)Ú(x4/y3) | — | — |
| q4 | x2/y1 | x3/y2 | — | x1/y2 |

Граф недетерминированного автомата Мили.
Не определены переходы из состояния q2 для символа x1, из состояния q3 для x2 и из состояния q4 для x4 и значения символов на выходе для (q1, x2), для (q2, x4) и для (q3, x2).
Для поиска слов b, генерируемых недетерминированным автоматом Мура также необходимо проследить последовательность изменения состояний автомата для каждого очередного символа слова.
пусть q1=q0 и a= (x1x2x3x3x3x2x4x4), тогда
a[t]: x1[1] x2[2] x3[3] x3[4] x3[5] x2[6] x4[7] x4[8]
q[t+1]: q1[1] q2[2] q4[3] q2[4] q1[5] q4[6] q1[7] q1[8] q1[9]
b[t]: y1[1] y1[2] y2[3] y2[4] y1[5] y1[6] y3[7] y3[8],
то есть b=(y1y1y2y2y1y1y3y3);
пусть q1=q0 и a= (x2x2x3x4x4x3x2x1), тогда
a[t]: x2[1] x2[2] x3[3] …
q[t+1]: q1[1] q3[2] * …
b[t]: *[1] *[2] …,
то есть b=(* * … и автомат "зависает" на третьем символе слова a;
пусть q1=q0 и a= (x1x4x3x2x3x2x4x4), тогда
a[t]: x1[1] x4[2] x3[3] x2[4] x3[5] x2[6] x4[7] x4[8]
q[t+1]: q1[1] q2[2] q2[3] q1[4] q3[5] q1[6] q3[7] q2[8] q2[9]
b[t]: y1[1] *[2] y2[3] * [4] y1[5] * [6] y3[7] * [8],
то есть b=(y1*y2*y1*y3*) содержит четыре символа "*";
Пример: дана таблица поведения недетерминированного автомата Мура. Составить таблицу соединений автомата и начертить граф. Найти генерируемые автоматом слова b для различных начальных состояний.
| y: (QÄX)®Q; j: Q®Y | |||||||
| qÎQ | xÎX | yÎY | |||||
| x1 | x2 | x3 | xn | ||||
| q1 | q2 | q3 | q4 | q1 | y1 | ||
| q2 | * | q4 | q1 | q2 | * | ||
| q3 | q2 | * | q1 | q2 | y2 | ||
| qm | q4 | q1 | q2 | * | y1 | ||
| Таблица соединений автомата | |||||
| qÎQ | qÎQ | yÎY | |||
| q1 | q2 | q3 | q4 | ||
| q1 | x4 | x1 | x2 | x3 | y1 |
| q2 | x3 | x4 | * | x2 | * |
| q3 | x3 | (x1Úx4) | * | — | y2 |
| q4 | x2 | x3 | — | x1 | y1 |
Следует отметить, что не определены переходы из состояния q2 для входного символа x1, из состояния q3 для входного символа x2 и из состояния q4 для входного символа x4. Не определено также значение символа на выходе для состояния q2.
Для поиска слов b при различных начальных условиях необходимо проследить всю последовательность изменения состояний автомата для каждого очередного символа слова a:
пусть q1=q0 и a=(x2x3x2x3x3x1x2x4), тогда
a[t]: x2[1] x3[2] x2[3] x3[4] x3[5] x1[6] x2[7] x4[8]
q[t+1]: q1[1] q3[2] q1[3] q3[4] q1[5] q4[6] q4[7] q1[8] q1[9]
b[t]: y1[1] y2[2] y1[3] y2[4] y1[5] y1[6] y1[7] y1[8],
то есть b=(y1y2y1y2y1y1y1y1);
пусть q2=q0 и a=(x2x3x1x4x4x3x2x1), тогда
a[t]: x2[1] x3[2] x1[3] x4[4] …
q[t+1]: q2[1] q4[2] q2[3]* [4] …
b[t]: *1] y1[2] * [3] …,
то есть b=(* y1* …) и автомат "зависает" на четвертом символе.
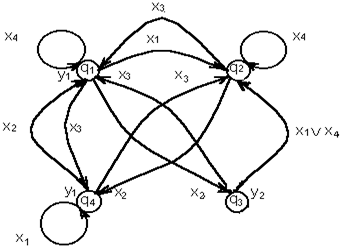
Граф недетерминированного автомата Мура
|
|
|


