 |
Глава 5. Основы теории алгоритмов
|
|
|
|
Понятие "алгоритм" принадлежит к числу основных понятий математики и занимает одно из центральных мест в вычислительной математике и проектировании разнообразных дискретных устройств.
Еще в IX веке узбекский ученый Мухаммед бен-муса аль-Хорезми разработал систему правил четырех арифметических действий над числами в десятичной позиционной системе счисления. Эти правила предписывали строгую последовательность действий над числами для получения искомого результата. Эти правила получили название "алгоритм" в честь арабского имени аль-Хорезми.
В ХХ веке в связи с развитием вычислительных машин и техники управления понятие алгоритма расширило свои границы. Так, основными объектами алгоритма стали разнообразные данные. Для уточнения понятия данные фиксируют конечный алфавит исходных символов (цифр, букв и т.п.) и правил построения алгоритмических объектов. Такими объектами стали числа и многочлены, кортежи и матрицы, графы и автоматы, слова и тексты.
Процесс преобразования алгоритмических объектов от исходных данных до искомого результата выполняется дискретно, как говорят, "по шагам". Происходящее за один шаг преобразование алгоритмического объекта носит локальный характер, т.е. преобразованию подвергается не весь объект, а лишь часть: член многочлена, компонента кортежа, столбец или строка матрицы, фрагмент графа или автомата, часть слова или текста и т.п. Процесс преобразования алгоритмического объекта, включающий в себя заданную последовательность шагов, называют алгоритмическим процессом.
В процессе развития теории алгоритмов были сформулированы основные свойства алгоритма:
· Свойство дискретности: алгоритм состоит из отдельных элементарных действий, выполняемых по шагам; множество элементарных шагов, из которых состоит алгоритмический процесс, конечно и счетно; типичным примером элементарных шагов является система команд компьютера.
|
|
|
· Свойство детерминированности: после каждого шага дается точное указание, как и в какой последовательности выполнять следующие шаги алгоритмического процесса.
· Свойство массовости: использование алгоритма допустимо для множества алгоритмических объектов заданного типа и заданного класса задач.
· Свойство результативности: обязательна остановка алгоритмического процесса после конечного числа шагов с указанием искомого результата.
Механизм алгоритмического процесса использует конечный набор элементарных объектов и конечный набор элементарных шагов. Эти наборы составляют основу алгоритмической модели. Для различных наборов элементарных действий могут быть сформированы различные алгоритмические модели.
Выделяют три основных типа алгоритмических моделей.
Первый тип — рекурсивные функции — связывает понятие алгоритма с числовыми функциями на множестве целых положительных чисел и принимающими значения на том же множестве.
Второй тип — машина Тьюринга — связывает понятие алгоритма с механическим устройством, способным выполнять дискретно элементарные действия над элементарными объектами.
Третий тип — нормальный алгоритм Маркова — связывает понятие алгоритма с классом словарных преобразований в результате замены части слова или всего слова другим.
В теории вычислительных алгоритмов доказана сводимость одного типа модели к другой, т.е. всякий алгоритм, описанный средствами одной модели, может быть описан средствами другой.
Рассмотрим подробнее реализацию алгоритмических процессов для вычисления значений числовых функций на трех типах моделей алгоритмов.
|
|
|
Рекурсивные функции
Рекурсия есть способ вычисления значения функции по известным значениям аргументов и известным значениям функции в некоторых предшествующих точках.
Если речь идет о числовых функциях, области определения и значения которых заданы на множестве целых положительных чисел, это описание рекурсии задает способ ее вычисления для заданного набора числовых значений аргументов и числового значения этой функции в некоторой исходной точке.
Числовые функции, для которых существует алгоритм вычисления их значений, называют рекурсивными функциями.
Если числовая функция определена не для всех значений аргументов, ее называют частично рекурсивной функцией.
Если для всех значений - то общерекурсивной функцией.
Любое вещественное число может быть синтаксически представлено цепочкой <целое> ". " <целое>, для которой существует только одна синтаксическая переменная — <целое>.
Следовательно, любую функцию можно свести к рекурсивной, если значения аргументов и значения функции рассматривать как значения, принадлежащие синтаксической переменной <целое>.
Для формирования механизма рекурсивных функций заданы наборы элементарных объектов - три базовые функции: константы, тождества и следования и наборы элементарных шагов – три элементарные операции: суперпозиции, рекурсии и минимизации.
Базовые функции
Функция константа. Если f={(x1, x2,... xn, у)| xiÎX; yÎY} =Cn, то любым значениям аргументов функции ставится в соответствие ее значение, равное постоянной величине — Сn. Чаще всего Cn=0.
Например,
если f ={(x1, x2, x3, у)} = C3, то для x1 = 5, x2 = 4, x3=7 и C3=0имеем у = 0.
Функция тождества или выбора аргумента. Если f = {(x1, x2,... xn, у) | xiÎX; yÎY} =J n;m, то любым значениям переменных аргумента функции ставится в соответствие ее значение, равное значению m-го независимого аргумента, где 1£ m £ n - номер независимого аргумента.
Например,
если f ={(x1, x2, x3, у)} = J3,2, то для x1 = 5, x2 = 4, x3 = 7 имеем у = 4;
если f={(x1, x2,, x3, у)} = J3,3, то для x1 = 5, x2 = 4, x3 = 7 имеем у = 7.
Функция следования. Если f ={(x, у)} = l(x), то любому значению независимой аргумента ставится в соответствие значение функции, равное числу, непосредственно следующим за числом, являющимся значением независимой аргумента.
|
|
|
Например,
если f = {(x, у)} = l(x), то для x = 5 имеем у = (х+1) = (5+1) = 6;
если f = {(x, у)} = l(x), то для x = 7 имеем у = (х+1) = (7+1) = 8.
Элементарные операции
Простейшие операции, с помощью которых из базовых функций могут быть получены рекурсивные функции, называют элементарными.
Операция суперпозиции. Если даны функция h от m независимых переменных аргумента, т.е. h = (z1, z2,...zm,, у), и m функций qi от n независимых переменных аргумента, т.е. qi = {(x1i, x2i,...xni, zij)}, то в результате подстановки функций q1, q2... qm вместо аргументов функции h может быть получена новая функция f = (x1, x2,...xn, у) от n независимых переменных аргумента, т.е.
h = (zi, z2,...zm, y);
q1 = (x1, x2,...xn, z1);
q2 = (x1, x2,...xn, z2);
...........................
qm=(x1, x2,...xn, zm)...
 |
h = (q1, q2,...qm, y) = f = (x1, x2,...xn, y).
Значения функций q1, q2,...qn, найденные для заданных значений независимых переменных x1, x2,...xn, принять за значения независимых переменных аргумента функции h и вычислить ее значение, которое принять за значение функции f = (x1; x2;... xn; y).
Например,
если h = (z, y) = l(z) и q = (х, z) = l(х), то f = (q, у) = l(l) = l2(х).
Следовательно, для x = 5 имеем z = 5+1 = 6 и у = 6+1= 7.
Оператор суперпозиции записывают так:
f =(x1, x2,...xn, y) = Smn(h(m), q1(n), q2(n),...qm(n)),
где h(m) = (z1, z2,...zm, y) и q1(n) = (x1i (n), x2i (n),...xni (n), zi).
Если заданы функции тождества (In,m) и оператор суперпозиции (Smn), то заданными являются любые операторы подстановки, перестановки и переименования любых функций.
Операция рекурсии. Если даны n-местная рекурсивная функция g и (n+2)-местная рекурсивная функция h, то можно найти (n+1)-местную рекурсивную функцию f, используя схему примитивной рекурсии:
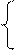f(x1, x2,...xn, 0) = g(x1, x2,...xn);
f(x1, x2,...xn, у+1) = h(x1, x2,...xn, у, f(x1, x2,...xn, у)).
Схема примитивной рекурсии имеет главный дополнительный аргумент — у, который определяет значение функции, и вспомогательный аргумент — f (x1, x2,...xn, у), который необходим для вычисления последующих значений главного дополнительного аргумента.
Оператор рекурсии записывают так:
f = (x1, x2,...xn, у+1) = R (g(n), h(n+2)),
где gi(n)=gi (x1, x2,...xn) и h(n+2)=h(x1, x2,...xn, у, f(x1, x2,...xn, у)).
При исполнении операции рекурсии x1 = a1, x2 = a2,...xn = an.
|
|
|
Значением искомой функции f для нулевого значения главного дополнительного аргумента следует считать значение функции g, а значением функции f для каждого последующего значения главного аргумента (у+1) следует считать значения функции h при предыдущих значениях главного аргумента у и при значении вспомогательного аргумента, совпадающим с предыдущим значением искомой функции.
Функции, для вычисления значений которых использовали базовые функции и операторы суперпозиции и примитивной рекурсии, называют примитивно-рекурсивными функциями.
Для вычисления функции предшествования
y - 1 при у>1; 
l-1(y)=(y 
1)=
0 при у £ 1,
по схеме примитивной рекурсии использованы функции g(х)=Ci(х)=0 и h(x, у, f (x, у))=J3,2=y, т. е.
f (x, 0)=g(x) = 0;
f (x, у+1) = h(x, у, f(x, у))= у.
Так как функции g и h не содержат в качестве аргумента независимую переменную х, то имеем:
f(0)=0;
f(1)=0;
f(2)=1;
f(3)=2...
f (i) = (i - 1).
Если i = у, то f(у) = (у - 1)=l-1(у).
Пусть у=6, тогда f(6)=6-1=5.
Таким образом, используя базовые функции константу и тождество, по схеме примитивной рекурсии может быть получено значение примитивно-рекурсивной функции предшествования:
l-1(у)= (у 
1)= R(0, у)
Для вычисления функции сложения целых чисел f+(x, y)=(x+y) по схеме примитивной рекурсии использованы базовые функции g(x)=J1,1=x и h(x, у, f(x, у)) = l(J3,3) = f(x, у)+1, т. е.
f(x, 0)=g(x) = x;
f(x, у+1)=h(x, у, f(x, у))= f(x, у)+1.
По схеме примитивной рекурсии имеем:
f(x, 0)=g(x)=x;
f(x, 1)=h(x, 0, f (x, 0))=x+1;
f(x, 2)=h(x, 1, f(x, 1))=x+2;
f(x, 3) = h(x, 2, f(x, 2)) = x+3...
f(x, i)=h(x, (i-1), f(x, (i-1)))=x+i.
Если i=у, то f+(x, у)=(x+у).
Пусть x=3, у=6, тогда f(3, 6)=3+6=9.
Таким образом, используя базовые функции тождества и следования, по схеме примитивной рекурсии может быть получено значение примитивно-рекурсивной функции сложения:
f+(x, у)= (x+y)=R(x, (f(x, у)+1)).
Для вычисления функции усеченного вычитания
x - у при x>y;
f(x, y)=(x y)=
0 при x £ y
по схеме примитивной рекурсии использованы g(x)=J1,1=x и
l-1(J3,3) = f(x, у) – 1, т. е.
f(x, 0)=g(x)=x;
f(x, 1)=h(x, 0, f(x, 0))=x-1;
f(x, 2)=h(x, 1, f(x, 1))=(x-1)-1=x-2;
f(x, 3) = h(x, 2, f(x, 2)) = (x-2)-2=x-3...
f(x, i)=h(x, (i-1), f(x, (i-1)))=(x-(i-1))-1=x-1.
Если i=у, то f(x, у)=(x-у).
Пусть х=6, y=3, тогда f(6, 3)=6-3=3.
Таким образом, используя базовую функцию тождества и примитивно-рекурсивную функцию предшествования, может быть получено значение примитивно-рекурсивной функции усеченного вычитания:
(x у)= R(x, (l-1(f(x, у)))) = f-(x, у).
Для вычисления функции умножения целых чисел 
по схеме примитивной рекурсии использованы базовая функция константа g(x)=С1=0 и примитивно-рекурсивная функция сложения h(x, у, f(x, у)) = f+(I3,1, I3,3 ) = x+f(x, у), т. е.
f(x, 0)=g(x)=0;
f(x, 1)=h(x, 0, f(x, 0))=x+0=x;
f(x, 2)=h(x, 1, f(x, 1))=(x+x)=2x;
f(x, 3) = h(x, 2, f(x, 2)) = (x+2x)=3...
f(x, i)=h(x, (i-1), f(x, (i-1)))=(x+(i-1))-x=i×x.
Если i=у, то f(x, у)=x × у.
|
|
|
Пусть х=3, y=4, тогда f(3, 4)=3 . 4=12.
Таким образом, используя базовые функции константы, тождества и примитивно-рекурсивную функцию сложения, может быть получено значение примитивно-рекурсивной функции умножения:
x×у = R (0, f+(x, f(x, у)))=f+(x, у).
Для вычисления функции возведения в степень fexp(x, y)= xy по схеме примитивной рекурсии использована базовая функция g(x)=С1=1 и примитивно-рекурсивная функция умножения
h(x, у, f(x, у)) = f * (I3,1, I3,3 ) = x×f(x, у), т. е.
f(x, 0)=g(x) = 1;
f(x, 1)=h(x, 0, f(x, 0))=x×1= x;
f(x, 2)=h(x, 1, f(x, l))=x×x=x2;
f(x, 3) = h(x, 2, f(x, 2))=x×x2 = x3...
f(x, i)=h(x, (i-1), f(x, (i-1)))=x×x(i - 1)=xi.
Если i=у, то f(x, y)=xy.
Пусть x=3, у=3, тогда f(3, 3)=33 =27.
Таким образом, используя базовую функцию константы и примитивно-рекурсивную функцию умножения, может быть получено значение примитивно-рекурсивной функции возведения в степень:
xy =R(1, f×(x, f(x, y)))=fexp(x, y).
Из приведенных примеров легко можно получить примитивно рекурсивные функции:
a) min(x, у)=x-(x-у)=f-(x, f-(x, y));
b) max(x, у)=у-(x-у)=f-(y, f-(x, y));
c) |х-у|=(х-у)+(у-х)=f+(f-(x, y), f-(y,x));
d) xvy = max(x, у);
e) х&у=min(х, у) и др.
Последовательность рекурсивного описания функции, использующая базовые функции и результаты вычисления ее значений на всех предшествующих точках с помощью операторов суперпозиции и примитивной рекурсии, называют протоколом.
Операция минимизации (поиск наименьшего корня): Если дана (n+1)-местная функция f(x1, x2,...xn, у), то значение n-местной функции j(x1, x2,...xn) можно определить, придавая вспомогательному аргументу у последовательно значения 0, 1, 2, 3,.., пока не окажется, что функция
f(x1, x2,...xn, у) в первый раз (!) стала равной нулю, т.е. f(x1, x2,...xn, у)=0.
Полученное значение вспомогательного аргумента у принять за значение определяемой функции, соответствующей заданным значениям независимых переменных аргумента (x1=a1, x2=a2,...xn=an).
Поиск значений функции j(x1, x2,...xn) выполняется с помощью m - оператора, который имеет вид:
j(x1, x2,...xn)=my(f(x1, x2,...xn, y)=0.
Пример: пусть f(x1, x2,...xn, у)=f(x1, x2, у)=x1×у-x2.
Тогда j(x1, x2)=my(f(x1, x2, у))=x1 × у-x2= 0 или j(x1, x2)= y =(x2/ x1).
Так как j(x1, x2) является рекурсивной функцией, то (x2/x1) должна иметь наименьшим общим кратным значение x1 для значения x2, что принято обозначать так: j(x1, x2)=[x2/ x1]. В противном случае j(x1, x2) - не определена. Например, если x1=3, то j(3, x2) определена только для значений x2 =3, 6, 9, 12,... и имеет значение 1, 2, 3, 4,... соответственно. Таким образом, функция j(x1, x2) является частично-рекурсивной.
Пример: пусть f (x1, x2,...xn, у)=f(x, у)=y2 -x.
Тогда j(x)=my(j(x, y))=y2-x = 0 или j(x)=y=Öx.
Так как j(x) является рекурсивной функцией, то Öx должен иметь значения только из множества целых положительных чисел, т. е. j(x)=1, 2, 3, 4,...
Если дан алгоритм вычисления функции f(a1, a2,...an, у), то значение функции j(a1, a2,...an) вычисляется следующим образом:
шаг 1: принять у=0 и вычислить функцию f(a1, a2,...an, у).
шаг 2: если f(a1, a2,...an, у)=0, то конец и значение функции
j(a1, a2,...an)=у, иначе принять у=у+1 и перейти к шагу 1.
Пример: пусть f(a1, a2,...an, у)=(x1 v x2 v x3v y) для x1=7, x2 =1, x3 =2.
По данному алгоритму имеем:
f(7, 1, 2, 0) = 7 - 1 - 2 - 0 ¹ 0;
f(7, 1, 2, 1) = 7 - 1 - 2 - 1 ¹ 0;
f(7, 1, 2, 2) = 7 - 1 - 2 - 2 ¹ 0;
f(7, 1, 2, 3) = 7 - 1 - 2 - 3 ¹ 0;
f(7, 1, 2, 4) = 7 - 1 - 2 - 4 = 0.
Следовательно, j(x1, x2,...xn) = j(7, 1, 2)=4.
Машина Тьюринга
Основные свойства алгоритма дискретности, детерминизма, массовости и результативности позволяют представить процесс вычисления какой-либо числовой функции с помощью математической машины. Эта машина за конечное число шагов из исходных числовых данных в соответствии с заданными правилами может получить искомый числовой результат.
Такая модель алгоритма была предложена английским математиком Тьюрингом в конце 30-х годов прошлого столетия, что почти на два десятилетия опередило появление электронных вычислительных машин и послужило их теоретическим прообразом.
Машина Тьюринга состоит из информационной ленты, считывающей и записывающей головки и управляющего устройства (рис. 5.1).
Информационная лента бесконечной длины представляет собой последовательность ячеек, в каждую из которых записан в точности только один символ из множества символов алфавита Vt={a1, a2...an}. Последовательность символов на ленте формирует слово a=(a1 a2... a|). Пробел между словами также является символом множества Vt. Например, # Î Vt.
С точки зрения формальных грамматик множество символов алфавита Vt есть множество терминальных символов.
Информационная лента исполняет функции внешней памяти машины Тьюринга.
Считывающая - записывающая головка обозревает одну ячейку информационной ленты, передает информацию о ее содержимом в управляющее устройство, и по указанию последнего сохраняет или изменяет содержимое ячейки.
Управляющее устройство представляет собой механизм, который на каждом шаге вычисления находится в одном из множества состояний Q = {q1, q2,...qm}. В зависимости от состояния qi и считанного символа aj управляющее устройство формирует команду на стирание или запись нужного символа в обозреваемую ячейку, перевод управляющего устройства в новое состояние и перемещение головки на соседнюю ячейку информационной ленты. Понятие "состояние" формирует "память машины Тьюринга", т.е. учет всех промежуточных состояний, которые привели машину в текущее состояние qi. Поэтому множество состояний управляющего устройства называют внутренней памятью машины Тьюринга. С позиции формальных грамматик множество символов состояний управляющего устройства есть множество нетерминальных символов. Среди всех состояний управляющего устройства следует выделить qo — начальное состояние ("старт") и qk — конечное состояние, ("стоп"), что облегчит формализацию протоколов машин Тьюринга и их композицию.
Для формализации перемещений головки относительно информационной ленты введем дополнительный алфавит D = {П, Л, С}, где П — означает перемещение головки вправо на одну ячейку информационной ленты, Л — влево на одну ячейку и С — останов.
Работа машины Тьюринга состоит в многократном повторении следующего цикла элементарных действий:
действие первое: считывание символа aj, находящегося под считывающей головкой;
действие второе: поиск команды, отвечающей текущему состоянию управляющего устройства qi, и считанному символу aj, т.е.
qj aj => q| am D;
действие третье: исполнение найденной команды, т.е. запись в обозреваемую ячейку символа am, перевод управляющего устройства в состояние qi и перемещение головки на соседнюю ячейку информационной ленты D.
Эти три действия формируют элементарный шаг алгоритмического процесса.
Последовательность команд для реализации процесса вычисления формирует протокол машины Тьюринга или программу алгоритмического процесса.
Следует отметить, что никакие две команды не могут иметь одинаковую пару текущего состояния qi и считываемого символа aj, т.е. (qi aj). Машина Тьюринга останавливается только в том случае, если на очередном шаге управляющее устройство генерирует состояние qk Результатом работы машины Тьюринга будет заключительное слово на информационной ленте
Описание машины Тьюринга
Математическая модель машины Тьюринга имеет вид:
Т =< Vt; Q; D; j; y; x >,
| где VT = {ai; a2;... an} | - символы внешней памяти; |
| Q = {qo, qi; q2;... qm} | - символы внутренней памяти; |
| D = {П; Л; С} | - символы перемещения головки; |
| j: Q Ä Vt => Vt | - функция выхода машины Тьюринга; |
| y: Q Ä Vt => Q | - функция переходов машины Тьюринга. |
| x: Q Ä Vt => D | - функция перемещения головки машины Тьюринга. |
Описание машины Тьюринга определяется записью всех слов на информационной ленте, положением головки относительно ячеек информационной ленты и текущим состоянием управляющего устройства. Такое описание называют конфигурацией машины Тьюринга:
K = a qi b,
где a — слово, расположенное слева от головки;
b — слово, расположенное справа от головки;
qi — текущее состояние машины Тьюринга.
Символ ‘а’, находящийся в ячейке под считывающей головкой, является первым символом слова b, т.е. b = (aj g).
К незаключительной конфигурации может быть применима только одна команда, которая переводит машину в новую конфигурацию. Так реализуется дискретность и детерминизм алгоритмического процесса.
Для удобства анализа вычислительных алгоритмов математик Пост предложил ограничить множество символов внешнего алфавита Vt двумя символами, т.е. Vt = {|; #}, где "|" (палочка) есть символ унарного кода числа, а "#" (диеза или решетка) есть символ пробела между числами. При этом любое целое положительное число может быть представлено на информационной ленте последовательностью палочек, как это представлено в табл. 5.1.
Таблица 5.1
| Число в десятичной системе счисления | "Слово" в унарном коде на информационной ленте |
| | =1о | |
| ||=11+1 | |
Nbsp; i ... |=1i+1 Для упорядочения составления протоколов информационную ленту ограничивают только в одну сторону, т. е. существуют левые и правые полуленты. В зависимости от используемой полуленты приняты различные схемы записи конфигураций машины Тьюринга (табл. 2). Таблица 5.2 Стандартная Информационная полулента конфигурация правая левая Начальная qn|x 1+1# |x 2+ 1#...#|x n+ 1 |x 1+1# |x 2+ 1#...#|x nqn| Конечная qk|y + 1 |yqk| Работу машины Тьюринга удобно представлять протоколом, таблицей и графом. При протокольной записи все команды должны быть записаны упорядоченным списком. На заключительном шаге должно быть получено значение заданной функции, т. е. y=f(x1, x2,...xn). Например, 1) qnai —>qiajD; 2) qiak —>qjaiD; ................................. n) q|am—>qkanC. Таблица 5.3 При табличном описании каждая строка имеет имя текущего состояния машины, а столбец–имя символа внешней памяти. Тогда элементами таблицы являются правые части команд (qjaiD). Текущее Символы vt состояние аi ак ... am qn qiajD ... qi ... qjaiD ... ... ... ... ... ... qi ... ... ... qkanC Табличная форма описания машины более компактна и позволяет применить матричные методы анализа для оптимизации структуры алгоритма. При графовом представлении вершинами графа являются состояния машины Тьюринга, а дугами — переходы в те состояния, которые предусмотрены командой. При этом на дуге указывают считываемый символ /записываемый символы в обозреваемой ячейке и команда на перемещение головки (рис. 5.2). Граф машины Тьюринга, реализующей заданный алгоритм, часто называют граф-схемой алгоритма (ГСА).
Примеры машин Тьюринга
Рассмотрим машины Тьюринга, реализующие и обеспечивающие формирование рекурсивных функций.
T1:= базовая функция Сn=0 на правой полуленте:
T1: qо|x + 1# ® qk|#.
| Протокол T1. 1) qо|®q1# П; 2) q1|®q1# П; 3) q1#®q2# Л; 4) q2 #®qk|C. | Текущее | Символы vt |
| состояние | # | |
| qо | q1 # П | — |
| q1 | q1 # П | q2 #Л |
| q2 | — | qk |C |
Пусть x = 3. Тогда для C1(3)=0 на информационной ленте машины Тьюринга будут проведены следующие преобразования:
x= 3 x= 0
#
Qn q1 q1 q1 q2 qk T2:= базовая функция Сn=1 на правой полуленте: T2: qо|x + 1#®qk||#; Протокол T2. 1) qо|®q1# П; 2) q1|®q1# П; 3) q1#®q2# |Л; 4) q2 #®qk|C. Текущее Символы vt состояние # qо q1 #П — q1 q1 #П Q2 |Л q2 — q1 |C T3:= базовая функция l(x) = х+1 на правой полуленте: T3: qo | x+1#® qk |(õ+1)+1#. Протокол T2.. 1) qo| ® q1|П; 4) q2| ® q2|Л; 2) q1| ® q1|П; 5) q2# ® q3 # П; 3) q1 # ® q2|Л; 6) q3| ® qk|C; Текущее Символы vt состояние | # qí q1 | П - q1 q1 | П q2 | Л q2 q2 | Л q3 # П q3 qk | C - Пусть х=3. Тогда для l(3)=3+1=4 на информационной ленте машины Тьюринга будут проведены следующие преобразования: x=3 #
|# ® #
|# ®#
|# ® #
|# ®#
||# ® #
||# ® #
Q0 q1 q1 q1 q1 q2 q2 q2 x=4 #
|| # ® #
|| # ®#
|| # ®#
Q2 q2 q2 q3 qk T4:= базовая функция Im,n на правой полуленте: T4: qo|1x1+1 # |2x2+1 #...#|mxm+1#...#|nxn+1#®qk|xm+1#, где |i - слово на i-м месте информационной ленты, |xi+1 – число “палочек”. Чтобы найти на информационной ленте i-е слово, следует установить счетчик |m, указывающий место слова |mxm+1 в последовательности слов. T4’: qo|m #|1x1+1#|2x2+1#...#|mxm+1#|nxn+1 ® qk|mxm+1. Текущее Символы vt Это позволит при каждом проходе вправо, отмечая один символ в слове |m, удалять очередное слово |m-1, предшествующее |mxi+1. Для организации вычисления такой функции необходимо увеличить число символов алфавита внешней памяти, что позволит уменьшить число состояний управляющего устройства и упорядочить весь процесс вычисления. Пусть Vт = {|, #, (}. Считывающая головка находится под первым символом слова счетчика |m. состояние | # ) qo q1 #П - - q1 q1 |П q2)П - q2 q2 #П q3)Л - q3 - q3 #Л q4)Л q4 q4 |Л q5 # П - q5 q6 #П - q8 #П q6 q6 |П - q7)П q7 - q7 #П q2 #П q8 - q8 #П q9 #П q9 q9 |П q10 #П - q10 q10 #П q11 #П - q11 q10 #П q12 #Л - q12 q13 |Л q12 #Л - q13 q13 |Л q14 #П - q14 qk |C - - На рис. 5. 6 приведен граф, реализующий базовую функцию Im,n. При подаче команды “старт” стирается первый символ слова |m и начинается перемещение головки вправо. После прочтения всех символов слова |m по команде q1#®q2) П ставится скобка, закрывающая оставшиеся символы слова |m, и головка перемещается на слово |x1+1. По команде q2| ®q2#П стираются все символы слова |1x1+1 и ставится закрывающая скобка q2#®q3)Л. Начинается перемещение считывающей головки влево за очередным символом слова |m-2. Так организован цикл. Затем управляющее устройство стирает второе слово, третье и т. д. пока есть символы “|” в счетчике. После стирания всех символов в счетчике по команде q5)®q8#П головка стирает закрывающую скобку, пробегает все пробелы “#”, по команде q8)®q9#П фиксирует место слова |mxm+1, пробегает все символы слова |mxm+1 и продолжает удалять все слова справа от слова |mxm+1по командам q10|®q10#П и q11|®q10#П. Если при чтении ленты в соседних ячейках будут символы “#”, то конец и головка возвращается на первый символ слова |mxm+1 по командам: q11#®q12#Л, q12#®q12#Л, q12|®q13|Л, q13|®q13|Л, q13#®q14#П и q14|®qk|C. T5:= функция предшествования l-1(x) = х-1 на правой полуленте: T5: qí | x+1 # ® qk | (õ +1) - 1 #. Протокол T5: 1) qо|®q1|П; 5) q3|®q3|Л; 2) q1|®q1|П; 6) q3#®q4#П; 3) q1 #®q2#Л; 7) q4|®qk|C. 4) q2|®q3#Л; Текущее Символы vt состояние | # qо q1 | П - q1 q1 | П q2 # Л q2 q3 # Л - q3 q3 | Л q4 # П q4 qk | C - T6 копирование m раз слово |x+1 на правой полуленте: T6: qо|x+1# ® qk|1x +1#|2x+1 #..#|mx+1#. Для того, чтобы выполнить m копий, необходимо занести на информационную ленту счетчик., т.е. изменить начальную конфигурацию машины, определяющий число копий |m: T6: qо|m #|x+1# ® qk|1x +1 # |2x+1 #..#|mx+1#. При каждом проходе вправо в слове |m удаляется один символ, затем выполняется обычное копирование слова |x +1, маркируя каждый переносимый символ командой q2|®q3(П и закрывая слово |x+1 командой q3#q4(П. После переноса всех символов слова |x +1 головка возвращается на самый левый символ слова |m и стирает его. Пусть Vт.={|, #, (,)}. Текущее Символы vt состояние | # ( ) qо q1 #П - - q8 #П q1 q1 |П q2)П - q2)П q2 q3 (П - q2)П q2)П q3 q3 |П q4)П - q4)П q4 q4 |П q5 |Л - - q5 q5 |Л - q6 (П q5)Л q6 q3 (П - - q7)Л q7 q7 |Л q7 #П q7 (Л q7)Л q8 q9 |Л - q8 (П q8)П q9 qk |C q9 #П q9 |Л q9 #Л Процесс продолжается до тех пор, пока не будут удалены все символы в слове 1m. После этого следует удалить все вспомогательные символы "("и")" и поставить головку машины в начало первого слова |x+1. Множество команд представлены таблицей, а работа машины показана графом на рис. 5.6. T7:= перестановка слов на правой полуленте: T7: qо|x+1# |y+1# ® qk|y +1# |x+1#. Протокол T7: 1)qо| ®q1(П; 12)q4)®q4)Л; 2)q1| ®q1|П; 13)q5|®q1(П; 3)q1# ®q2)П; 14)q5)®q6)П; 4)q1) ®q2)П; 15)q6|®q6|П; 5)q2| ®q2|П; 16)q6)®q7# Л; 6)q2# ®q3)П; 17)q7|®q7|Л; 7)q2) ®q3)П; 18)q7(®q7#Л; 8)q3| ®q3|П; 19)q7)®q7#Л; 9)q4 # ®q4|Л; 20)q7#®q8#П; 10)q4| ®q4|Л; 21)q8# ®q8 #П; 11)q4(®q5(П; 22)q8|®qk|C. Текущее состояние Символы vt | # ( ) qо q1 (П - - - q1 q1 |П q2)П - q2)П q2 q2 |П q3)П - q3)П q3 q3 |П q4 |Л - - q4 q4 |Л - q5 (П q4)Л q5 q1 (П - - q6)П q6 q6 |П - - q7 #Л q7 q7 |Л q7 #П q7 #Л q7 #Л q8 qk |C q8 #П - - T8:= сравнение длины двух слов на правой полуленте: T 8(1): qo1x+1 #|y+1®qk1|(x - y) при x > y; T8(2): qo1x+1 #|y+1®qk3| при x = y; T8(3): qo |x+1 #|y+1 ®qk2| (y - x) при x < y. В таблице приведен набор команд, реализующих поставленную задачу, а ниже - граф, иллюстрирующий работу алгоритма. таблица Продолжение таблицы Тек-е сост-е Символы vt Тек-е сост-е Символы vt | # ) | # ) qо q1 #П - q4 q4 |Л q5 #П q4)Л q1 q1 |П q2)П q2)П q5 q1 #П - q8 #П q2 q2 |П q3 #Л - q6 q6 |Л q7 #П - q3 q4 #Л - q6 #Л q7 qk1 |C - - q8 qk2 |C qk3 |C - T9:= устранение пробелов между словами на правой полуленте: Т9:qo|x1+1##...#|x2+1# ®qk|x1+1# |x2+1#. Для реализации алгоритма необходим алфавит Vt = {|, #,)}. После просмотра символов первого слова ставится “)” для ограничения переноса символов второго слова. текущее состояние Символы алфавита Vt Последний символ второго слова также замещается “)” для ограничения движения вправо. После переноса всех символов второго слова устраняются “)”, и считывающая головка возвращается на первый символ первого слова. | # ) qo q1 |П - - q1 q1 |П q2)П - q2 q3 |П q2 #П q7 #Л q3 q3 |П q4 #Л q4 #Л q4 q5)Л - - q5 q5 |Л q5 #Л q6)П q6 q6 |П q2 |П - q7 q7 |Л q7 #Л q8 #Л q8 q8 |Л q9#П - q9 qk|С - - T10:= поиск последнего слова на правой полуленте: T10: qo|x1+1#|x2+1#... # |xm+1 ® |x1+1#|x2+1#... # qk|xm+1. Поиск крайнего правого слова на информационной полуленте завершается после нахождения не менее двух рядом стоящих #. Затем считывающая головка возвращается на первый символ последнего слова. На рис. 5.12 представлен граф алгоритма. Текущее состояние Символы Vt | # qo q1|П - q1 q1|П q2#П q2 q1|П q3#Л q3 q4|Л q3#Л q4 q4|Л q5#П q5 qk|C - T11:= вычисление усеченного вычитания. qk1|x-y#, если x>y; Т11: qo|x+1# |y+1# ® qk2|, если x£y. Для вычисления на машине Тьюринга усеченного вычитания можно использовать машины Т8 и Т1, изменив команды машины Т8: q8|®qk2|C и q8#®qk3|C на команды машины Т1:q8|®q8#П, q8#П®q8#П (состояния q1 и q2 машины Т1 есть, соответственно, q8 и q9 машины T11). Текущее Символы vt состояние | # ) qо q1 #П - q1 q1 |П q2)П q2)П q2 q2 |П q3 #Л - q3 q4 #Л - q6 #Л q4 q4 |Л q5 #П q4)Л q5 q1 #П - q8 #П q6 q6 |Л q7 #П - q7 qk1 |C - - q8 q9#П q9#П - q9 - qk2|C - Т12:= вычисление предиката: qk||, если Р(x, y):= “истина”, Т12: qo|x+1# |y+1#...® qk|, если Р(x, y):= “ложь”. Для этого можно использовать машины Тьюринга Т8, Т1 и Т2.
Композиция машин Тьюринга
Для графического изображения основных операций алгоритма приняты обозначения блоков, показанные на рис. 5.15
Последовательное и/или параллельное соединение различных блоков позволяет организовать вычисление любых частично-рекурсивных функций. Общую схему соединения нескольких блоков от “начало” до “конец” называют блок-схемой алгоритма.
О ператор суперпозиции. Если даны m-местная функция h=(z1, z2,...zm, у) и m n-местных функций gi=(x1, х2,....хn, zi), где 1£ i £m, которые вычислимы по Тьюрингу, то функция f=(x1, х2,...хn, у) также вычислима на машине Тьюринга.
Рассмотрим машину Тьюринга только для одного случая, когда n=1 и m=1. Тогда f=(x, y)=S11 h((z, y), g(x, z)).
Для того, чтобы вычислить по заданным значениям x функцию у=f(х), необходимо и достаточно вычислить значение z=g(х), а по ее значениям вычислить y=h(z)=h(g(х))=f(x).
Таким образом, если h=(z, у) и g=(х, z) вычислимы по Тьюрингу, то их суперпозиция h(g(х))=f(х)=у также вычислима.
Весь процесс вычисления опирается на две машины Тьюринга:
шаг 1: вычислить для х значение z=g (х):
Tg: qí|x+1®qk|g (x+1) +1.
шаг 2: вычислить для z=g(х) значение y=h(g(х)):
Th : qí|g (x+1) +1®qk|h (g (x+1)) +1.
Вычисленное значение функции h есть значение искомой функции, т.е. y=f(x)=h(g(x)).
Если каждый шаг вычислительного процесса представить отдельной машиной Тьюринга, то их последовательное соединение исполняет оператор суперпозиции.
Если п ¹ 1и m ¹ 1, то необходимо вычислять m функций gi,, каждая из которых опирается на n независимых переменных xi, а затем значения этих функций использовать в качестве независимых переменных zi функции h.
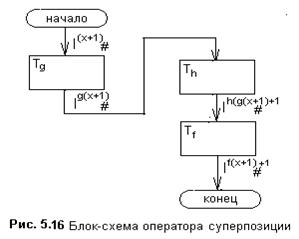
Алгоритм вычисления оператора суперпозиции :
шаг 1: вычислить для заданных значений x1, х2,...хn функции
gi (x1, х2,...хn), где I £ i £ m:
Tg:qо|x1+1 #|x2+1#...#|xn+1® qk|g1(x1+1, x2 +1,.. xn+1)+1#..|gm (x1+1, x2+1,... xn+1) +1;
шаг 2: вычислить для полученных значений gi (x1, х2,...хn) функцию
h(g1, g2,...gn):
Th:qо|g1(x1+1, x2+1,.. xn+1) +1 #...|gm(x1+1, x2+1,.. xn+1) +1®
® qk|h(g1+1, g2 +1,.. gm+1)+1.
Вычисленное значение функции h есть значение искомой функции у=f(x1, х2,...хn)=h(gi(x1, х2,...хn), g2(x1, х2,...хn),...gm(x1, х2,...хn)).
Оператор рекурсии. Если даны n-местная функция g(x
