Последовательное соединение автоматов

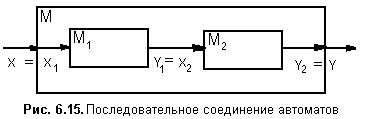
Пусть автоматы М₁ и М₂ соединены, как показано на рис. 6.15.

При этом X=X₁, Y₁=X₂, Q = (Q₁ÄQ₂) и Y=Y₂.

 

 

Функционирование автомата M может быть описано системой:

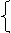q[t+1]=(q₁[t+1]; q₂[t+1])=(y₁(q₁[t]; x₁[t]); y₂(q₂[t]; j₁(q₁[t]; x₁[t])));

y[t]=j(q[t]; x[t])=j₂(q₂[t]; j₁(q₁; x₁).

По данным таблиц 6.27, 6.28 и 6.29 составим таблицу поведения автомата М (см. таблицу 6.30).

Последовательное соединение автоматов - некоммутативная операция. При смене мест автоматов М₁ и М₂ меняется структура автомата М и его поведение.

Пусть М1 находился в состоянии q11, а на его вход подан сигнал x11. М1 формирует на выходе сигнал y11=x21 и переходит в состояние q12.. М2 находился в состоянии q21, по сигналу x21 переходит в состояние q21 и формирует на выходе сигнал y21. Следовательно, автомат М переходит из состояния q1=(q11; q21) в состояние q3=(q12; q21) и генерирует на выходе сигнал y21.	таблицу 6.30
Автомат М
qÎQ	xÎX
x11	x12
q1	q3; y21	q1; y22
q2	q4; y21	q1; y22
q3	q6; y21	q3; y21
q4	q6; y21	q4; y21
q5	q5; y21	q1; y21
q6	q6; y21	q2; y21

Параллельное соединение автоматов

Параллельное соединение автоматов возможно в четырех вариантах (см. рис. 6.16).

Различие схем заключено в формировании входных и выходных сигналов.

Для схем а) и с), множество сигналов на входе автомата М определяется парой входных сигналов автоматов М₁ и М₂, то есть сигнал на входе есть вектор x_i= (x_1j; x_2k)Î(X₁ÄX₂) (см. таблицу 6.31).

Для схем а) и b) множество сигналов на выходе автомата М определяется парой выходных сигналов автоматов М₁ и М₂, то есть сигнал на выходе есть вектор y_i= (y_1j; y_2k)Î(Y ₁ÄY₂) (см. таблицу 6.32).

Для схем b) и d) сигналы на входе автомата М равны входным символам автоматов М₁ и М₂ при условии X₁=X₂=X.

Для схем с) и d) значения сигналов на выходе автомата М определяются оператором g, то есть y=g(y_1i, y_2j).

.

Таблица 6.31

x1	x2	x3	x4	x5	x6
(x11; x21)	(x11; x22)	(x11; x23)	(x12; x21)	(x12; x22)	(x12; x23)

 

Таблица 6.32

y1	y2	y3	y4	y5	y6
(y11;y21)	(y11;y22)	(y12;y21)	(y12;y22)	(y13;y21)	(y13;y22)

 

Система рекуррентных соотношений для схемы а) есть:

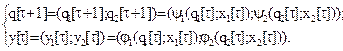
Это позволяет вычислить каждую позицию таблицы 33 поведения автомата М.

Например, если дано q₁=(q₁₁, q₂₁) и x₄=(x₁₂, x₂₁), то

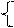q=(y₁(q₁₁, x₁₂); y₂(q₂₁, x₂₁))= (q₁₁, q₂₁)= q₁;

y=(j(q₁₁, x₁₂); j(q₂₁, x₂₁))= (y₁₃, y₂₁)=y_5.

(см. таблицы 27-29, 31, 32).

Таблица 6.33
текущее состояние	символы входного алфавита xÎX
x1	x2	x3	x4	x5	x6
q1	q3; y1	q4; y1	q3; y2	q1; y5	q2; y5	q1; y6
q2	q4; y1	q4; y1	q3; y2	q2; y5	q2; y5	q1; y6
q3	q5; y1	q6; y1	q5; y2	q3; y1	q4; y1	q3; y2
q4	q6; y1	q6; y1	q5; y2	q4; y1	q4; y1	q3; y2
q5	q5; y1	q6; y1	q5; y2	q1; y3	q2; y3	q1; y4
q6	q6; y1	q6; y1	q5; y2	q5; y3	q2; y1	q1; y4

Для схемы b) на входе автомата М есть x₁=x₁₁=x₂₁, x₂=x₁₂=x₂₂. Тогда система рекуррентных соотношений есть:

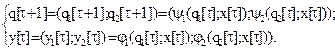
Это позволяет вычислить каждую позицию таблицы 34 поведения автомата М.

Например, если дано q₁=(q₁₁, q₂₁) и x₅=(x₁₂, x₂₂), то

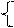q=(y₁(q₁₁, x₁₂); y₂(q₂₁, x₂₂))= (q₁₁, q₂₂)= q₂;

y=(j(q₁₁, x₁₂); j(q₂₁, x₂₂))= (y₁₃, y₂₁)=y_5.

(см. таблицы 27-29, 31, 32).

Таблица 6.34

текущее состояние	символы входного алфавита xÎX
x1	x5
q1	q3;y1	q2;y5
q2	q4;y1	q2;y5
q3	q5;y3	q1;y1
q4	q6;y3	q4;y1
q5	q5;y1	q2;y1
q6	q6;y1	q2;y1

Для схемы с) выход автомата М формируется функцией

y=g(y_1i; y_2j).

Рекуррентные соотношения для такого автомата M есть:

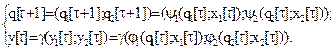
Оператор g формируется поставленной задачей.

Это позволяет вычислить каждую позицию таблицы 35 поведения автомата М.

Например, если дано q₁=(q₁₁, q₂₁), x₅=(x₁₂, x₂₂) и если аргумент функции g содержит символ y₂₁, то на выходе автомата М – формируется символ от автомата М₁, если - y₂₂, то - символ от автомата М₂, то

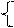q=(y₁(q₁₁, x₁₂); y₂(q₂₁, x₂₂))= (q₁₁, q₂₂)= q₂;

y=g(j(q₁₁, x₁₂); j(q₂₁, x₂₂))= (y₁₃, y₂₁)=y_13.

Таблица 6.35

текущее состояние	символы входного алфавита xÎX
x1	x2	x3	x4	x5	x6
q1	q3;y11	q4;y11	q3;y22	q1;y13	q2;y13	q1;y22
q2	q4;y11	q4;y11	q3;y22	q2;y13	q2;y13	q1;y22
q3	q5;y11	q6;y11	q5;y22	q3;y11	q4;y11	q3;y22
q4	q6;y11	q6;y11	q5;y22	q4;y11	q4;y11	q3;y22
q5	q5;y11	q6;y11	q5;y22	q1;y12	q2;y12	q1;y22
q6	q6;y11	q6;y11	q5;y22	q5;y12	q2;y11	q1;y22

Для автомата по схеме d) сигнал на входе формируется также как для автомата по схеме b), а сигнал на выходе также как для автомата по схеме с).

Система рекуррентных соотношений есть: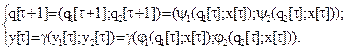

Например, если дано q₁=(q₁₁, q₂₁), x₅=(x₁₂, x₂₂) и если аргумент функции g содержит символ y₂₁, то на выходе автомата М – формируется символ от автомата М₁, если - y₂₂, то - символ от автомата М₂:

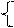q=(y₁(q₁₁, x₁₂); y₂(q₂₁, x₂₂))= (q₁₁, q₂₂)= q₂;

y=g(j(q₁₁, x₁₂); j(q₂₁, x₂₂))= (y₁₃, y₂₁)=y_13.

Таблица 6.36

текущее состояние	символы входного алфавита xÎX
x1	x5
q1	q3;y11	q2;y13
q2	q4;y11	q2;y13
q3	q5;y12	q1;y11
q4	q6;y12	q4;y11
q5	q5;y11	q2;y11
q6	q6;y11	q2;y11

 

Обратная связь автоматов

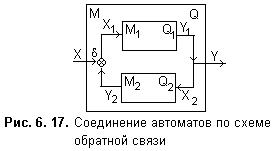
Автоматы М₁ и М₂ соединены так, как показано на рис. 6.17. При этом в обратной связи чаще всего применяют автомат Мура, поведение которого есть: 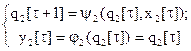при j₂=1.

Пусть таблицей 6.37 дано описание автомата Мура.

Таблица 6.37

текущее состояние	символы yÎY	Выход М2
y11=y1=x21	y12=y2=x22	y13=y3=x23
q21	q21	q22	q21	y21
q22	q22	q22	q21	y22

 

Для автомата М имеем Q=(Q₁ÄQ₂), Y₁=X₂=Y и d:(XÄY₂)®X₁.

Система рекуррентных соотношений для описания автомата М: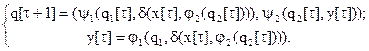

Оператор d: (XÄY₂)®X₁ формируется поставленной задачей.

Пусть он задан таблицей 6.38.

Таблица 6.38

символ xÎX	символ y2iÎY2
y21	y22
x1	x11	x12
x5	x12	x11

 

Поведение автомата М описано таблицей 6.39

В таблице символом "*" обозначены позиции, для которых нет элементов в области определения оператора d.

Например, согласно таблице 6.38, если q₁=(q₁₁, q₂₁) и x₁₁=(x₁, y₂₁) или x₁₁=(x₅, y₂₂), то

q=(y₁(q₁₁, x₁₁); y₂(q₂₁, y₁₁=x₂₁))= (q₁₂, q₂₁)= q₃;

y=j₁(q₁₁; x₁₁))=y₁₁ ,

или

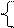q=(y₁(q₁₁, x₁₁); y₂(q₂₁, y₂₂))=(q₁₂, *)= *;

y=j1(q₁₁; x₁₁)=y₁₁ (см. таблицы 27-29, 31, 32).

Таблица 6.39
текущее состояние	аргумент функции d(x;j2(q2))
(x1; y21)	(x1; y22)	(x5; y21)	(x5; y22)
q1=(q11; q21)	q3; y11	*; y11	q1; y13	*;y13
q2=(q11; q22)	* y11	q1; y11	*; y13	q4; y13
q3=(q12; q21)	q6; y12	*; y11	q3; y11	*; y11
q4=(q12; q22)	*; y12	q4; y11	*; y11	q6; y11
q5=(q13; q21)	q5; y11	*; y11	q1; y11	*; y11
q6=(q13; q22)	*; y11	q2; y11	*;y11	q6; y11

Всякий автомат в синхронном режиме может быть реализован сетью, состоящей из комбинационных автоматов и элементов задержки. Автомат Мура формирует задержку на один такт

Сумма автоматов

При асинхронном режиме работы автоматов M₁ и M₂ внутренние состояния сети принадлежат множеству Q=(Q₁ÈQ₂).

Таблица 6.40

текущее состояние	символы входного алфавита xÎX=(X1ÈX2)
x11	x12	x21	x22	x23
q11	q12;y11	q11;y13	—	—	—
q12	q;y12	q12;y11	—	—	—
q	q;y11	q11;y11	q;y21	q22;y21	q;y22
q22	—	—	q22;y21	q22;y21	q;y22

 

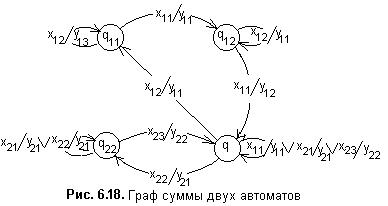
Для того, чтобы из двух автоматов сформировать сеть, необходимо определить заключительное состояние q_k первого в очереди автомата, начальное состояние q₀ следующего в очереди автомата и соединить эти состояния. В таблице 6.40 таким состоянием является q, принадлежащее двум автоматам.

⇐ Предыдущая25262728293031323334Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: