Контроль двух параллельно работающих элементов

Метод контроля по допуску на определяющий параметр в упрощенном виде можно распространить для контроля двух параллельно работающих взаимно резервируемых объектов. Сравнению подлежат выходные параметры у ₁и у ₂объектов (рис. 2.3). Разность этих параметров сравнивается с допуском Dу ₀. Если ïD у ï– ïD у ₀ï > 0, то выдается сигнал отказа.

 

Рис. 2.3 Схема контроля взаимно резервируемых объектов

 

Этот метод можно расширить, если в качестве второго объекта использовать физическую модель, которая моделирует передаточную функцию контролируемой части объекта. Кроме того, данный подход можно использовать и для проведения тестового диагностирования, если на вход диагностируемого объекта и модели подавать тестовое воздействие.

Контроль одинаковых объектов, работающих параллельно

В современных сложных системах управления и контроля широкое распространение имеет многократное резервирование наиболее ответственных агрегатов, т.е. имеет место несколько параллельно работающих каналов. Выходной сигнал каждого канала является средним значением сигналов трех независимых датчиков. Для получения среднего значения используется схема-кворум элемента (рис. 2.4).

 

Рис. 2.4 Контроль параллельно работающих объектов
на основе схемы-кворум элемента

 

Применение этой схемы также позволяет вести контроль за техническим состоянием параллельно работающих объектов. На входы каждого из N сумматоров, установленных за объектами контроля, подаются выходные сигналы у_i от объектов контроля и результат Y, получаемый на выходе сумматора С. На выходе каждого из N сумматоров получается разность e_i = у_i – Y,которая усиливается соответствующим усилителем. При равных коэффициентах усиления К

или

.

Преобразовывая это выражение относительно Y при условии, что
К >> 1, получим следующее выражение:

.

Из этого соотношения следует, что на выходе сумматора С в схеме кворум-элемента имеется среднее значение выходных сигналов контролируемых блоков. Контроль за техническим состоянием блоков ведется по значениям e _i. Если одно из значений превышает допуск, то этот канал неисправен. После отказа и выключения i -гo канала схема продолжает работать и контролировать состояние N– 1 каналов.

Логические методы контроля (знаковые)

Если объект контроля обладает линейной функцией преобразования входного сигнала в выходной, то знак приращения определяющего выходного параметра должен совпадать со знаком приращения входного параметра. В этом случае применяется правило знаков:

– если отклонение +D х (–D х) вызывает появление отклонения
+D у (–D у), то объект исправен;

– если отклонение –D х (+D х) вызывает появление отклонения
+D у (–D у), то объект неисправен.

Приведенные выше методы применимы в простейших случаях, когда можно выделять определенные параметры диагностирования. Если количество диагностируемых параметров велико и их связь с параметрами технического состояния неявна, то такие методы неприменимы. В этих случаях решение задач диагностики требует создания специальных математических (диагностических) моделей.

2.3 Контрольные вопросы к главе 2

1. На чем основаны физические методы диагностирования?

2. Назовите основные физические методы неразрушающего контроля.

3. На чем основаны виброакустические методы контроля и диагностики?

4. Нарисуйте схему контроля по допуску на определяющий параметр.

5. В каком случае возможно применение логических методов контроля?

 

ГЛАВА 3 МАТЕМАТИЧЕСКИЕ МОДЕЛИ
В ТЕХНИЧЕСКОЙ ДИАГНОСТИКЕ

 

Основные понятия

 

Решение задач технической диагностики требует анализа множества состояний, в которых объекты могут находиться в период эксплуатации, классификации этих состояний, выбора диагностических параметров и признаков, установления связи между конкретными значениями диагностических параметров (признаков) и конкретным техническим состоянием объекта, разработки решающего правила и алгоритма постановки диагноза. Решать эти задачи можно двумя путями: экспериментально или теоретически. Экспериментальный путь наиболее достоверен, поскольку в реальных условиях эксплуатации оценивается связь между диагностическими параметрами (признаками) и параметрами технического состояния. Следует отметить, что чисто экспериментальный путь решения задач диагностики невозможен.

Для решения указанных проблем теоретическим путем необходимо иметь формализованное описание связи между параметрами технического состояния и диагностическими параметрами или признаками, т.е. необходимо разрабатывать математические (диагностические) модели диагностируемых объектов.

Формализованное описание (математическая модель) объекта диагностирования может быть представлено в различной форме:

– в аналитической (в виде дифференциальных или алгебраических уравнений);

– в табличной форме (в виде таблицы состояний);

– в графической (в виде графов причинно-следственных связей);

– в форме логических соотношений и т.д. [1, 5, 7, 8, 10, 15, 19, 26, 27, 28].

Математические модели могут быть заданы в явном или неявном виде.

Явная модель объекта диагностирования включает в себя совокупность формализованных описаний всех оговоренных нормативной документацией технических состояний, которые подлежат диагностированию.

Неявная модель объекта технического диагностирования содержит формализованное описание одного технического состояния и правила получения описаний других технических состояний на основе заданного. Причем чаще всего математическая (диагностическая) модель определяет исправное состояние. Модели для других технических состояний получают на основе модели исправного состояния и правил, связывающих конкретную неисправность с параметрами технического состояния.

В общей постановке математическую модель объекта технической диагностики можно охарактеризовать следующим образом [17]. Пусть имеется объект, у которого техническое состояние описывается внутренними параметрами Z. На вход объекта подаются внешние возмущения X (входные параметры). На выходе объекта наблюдается отклик в виде выходных (диагностических) параметров Y. В самом общем случае соотношение между указанными параметрами устанавливают, вводя понятие оператор объекта диагностирования А (z, х). При этом математическая модель будет иметь следующий вид:

Y = A (Z, X). (3.1)

Вводя индексы i для разных состояний: 0 – исправное, i – i -e неисправное состояние; и индексы j для различных внешних возмущений, уравнение (3.1) можно переписать в виде системы уравнений:

Y ₀ ^j = A (Z ₀, X_j); Y _i ^j = А (Z_i, X_j), (3.2)

где i = 1... k; j = 1... m.

Система уравнений (3.2) состоит из k + 1 уравнений и представляет из себя явную математическую модель объекта диагностирования. Для упрощения записи внутренние параметры Z (параметры технического состояния) включают в оператор, и систему уравнений (3.2) при любом внешнем возмущении X записывают в виде

Y ₀ = A ₀(X); Y_i = A_i (X). (3.3)

Такой способ задания математической модели является весьма общим. Выбор конкретной формы оператора и есть выбор конкретной математической модели объекта диагностирования. Этот выбор зависит от физических свойств диагностируемого объекта, определяется условиями диагностической задачи и принятыми методами ее решения.

Объекты диагностирования в зависимости от своих свойств делятся на дискретные и непрерывные.

Объект считается непрерывным,если его оператор преобразует совокупность входных сигналов X, определенных на непрерывном (несчетном, континуальном) множестве, в совокупность выходных сигналов Y, принимающих значения на таких же множествах.

Объект считается дискретным,если он имеет оператор, который преобразует совокупность входных величин X, принимающих значение на конечных (счетных) множествах, в совокупность выходных величин Y, принимающих значения на таких же множествах.

Объект называется гибридным,если его оператор осуществляет преобразование непрерывного входного сигнала X в дискретный выходной сигнал Y или наоборот.

Для дискретных объектов разделение технических состояний, в которых он может находиться, на классы не представляет затруднений. Так как значения диагностических параметров и параметров технического состояния счетные, то счетным будет и количество классов технического состояния. Для непрерывных объектов при разделении технических состояний на классы возникают затруднения, связанные с непрерывностью диагностических параметров и бесконечным числом технических состояний.

Практически диагностическую задачу при бесконечном числе технических состояний решить невозможно. Поэтому в любом случае выделяется конечное множество технических состояний, которые требуется диагностировать. Таким образом, при практическом решении диагностической задачи оператор А (z, x) для непрерывных объектов заменяется гибридным, реализующим на выходе конечное множество значений диагностических признаков.

Для перехода от непрерывного множества технических состояний, которые есть на самом деле, к дискретному множеству технических состояний, которые можно диагностировать, вводится понятие «элементарная проверка объекта» [16, 17]. Элементарная проверка объекта (ЭПО) – это процедура подачи на объект отдельного (рабочего или тестового) воздействия и снятия с объекта соответствующего ответа (реакции). Поясним это понятие.

Пусть объект диагностики имеет точки контроля, которые позволяют наблюдать за входными X, внутренними Z и диагностическими Y параметрами. В соответствии с определением каждому входному возмущению X_j из множества входных возмущений X будет соответствовать элементарная проверка p _j из множества проверок П(p _j Î П), т.е. X_j → p _j в техническом состоянии s_i, из множества S (s_i Î S), входное воздействие на объект X соответствует этой проверке. Внутренние параметры Z и оператор А определяются техническим состоянием s_i из множества S (s_i Î S). Выходные диагностические параметры Y соответствуют результату j -й проверки, т.е. Y_i^j ® R_i^j. Тогда операторное выражение (3.3) в понятиях ЭПО для j -й проверки объекта, находящегося в i -м техническом состоянии, запишется следующим образом:

R_i^j = A_i (p _j), (3.4)

где j = 1... n; i = 0, 1... k.

Для исправного состояния это выражение часто записывается в виде

R^j = A (p _j). (3.5)

Выражения (3.4) и (3.5) определяют модель в явном виде. Если имеются зависимость вида (3.5) и правила, позволяющие из множества проверок П и состояний S получать совокупность выражений вида (3.4), то объект диагностирования задан неявной моделью.

Представленные модели объектов диагностики в операторном виде используются для формального описания диагностических задач в общей постановке, но они непригодны для решения конкретных диагностических задач. Для выполнения диагностирования на практике необходимо иметь математические (диагностические) модели в конкретном виде, т.е. необходимо для каждой практической задачи конкретизировать вид оператора А.

Наиболее простой формой представления оператора А в случае явной модели является табличная форма. Таблица строится следующим образом. Пусть каждому отказу (неисправности) объекта соответствует s_i неисправное состояние из множества S (i = l... n). Исправное состояние обозначим s ₀. Примем, что столбцы таблицы соответствуют возможным состояниям s_i Î S, а строки – проверкам p_jÎП. В клетку таблицы на пересечении i -гo столбца и j -й строки записывается результат R _i ^j проверки p_jобъекта диагностирования, находящегося в техническом состоянии s_i. Совокупность результатов образует множество R (R _i ^j Î R), число элементов этого множества г = n (k + l). Такая таблица называется таблицей состояний объекта диагностирования. Она эквивалентна выражениям (3.4) и (3.5).

Таблица 3.1

Таблица состояний объекта диагностирования

p\ s	s 0	s 1	…	s i	…	sk
p1	R 1	R 11		R 1 i		R 1 k
…
p j	R j	R j1		Rj i		Rjk
…
p n	R n	R n1		Rn i		Rnk

 

Анализ этой таблицы позволяет сформулировать свойства множества проверок П, необходимые для решения задач технического диагностирования.

Первое свойство:множество проверок П обнаружит любое неисправное состояние объекта диагностирования из множества S, если для каждого состояния s_i Î S найдется хотя бы одна проверка p_jÎП, такая, что R^j ¹ R^j_i. Это свойство эквивалентно тому, что столбец таблицы с s ₀ отличается от каждого из остальных с s_i. Такая таблица называется проверяющей или контролирующей.

Второе свойство:множество проверок П различают все состояния из множества S, если для каждой пары технических состояний s_i и s_m найдется хотя бы одна проверка p _j, такая, что R^j_i ¹ R^j_m. Это свойство таблицы эквивалентно тому, что все столбцы, определяющие различные состояния, попарно различимы. Такая таблица называется разделяющей.

Если таблица обладает только первым свойством, то она позволяет решать только задачи контроля. Если таблица обладает обоими свойствами, то она позволяет решать задачи диагностики.

Исходной информацией для составления таблицы состояний могут быть: структурные, функциональные, принципиальные схемы, причинно-следственные связи между параметрами технического состояния, входными и диагностическими параметрами. Одним из наиболее часто используемых способов построения таблицы состояния является построение этих таблиц на основе функциональных моделей [16, 17].

Функциональная модель

 

Если объект диагностики можно представить как несколько взаимосвязанных частей, имеющих самостоятельное функциональное значение, то в качестве математической (диагностической) модели применяется так называемая функциональная модель, пользуясь которой можно составить таблицу состояний.

Функциональная модель представляет собой графическое изображение объекта, в котором каждая выделенная часть (функциональный элемент) обозначается в виде прямоугольника со значком Q_i и этот прямоугольник имеет несколько входов x_j, но только один выход у_i (рис. 3.1).

 

Рис. 3.1 Элемент функциональной модели

 

Количество входов определяется числом внешних воздействий на конкретный элемент. Связи между элементами обозначаются линиями со стрелками, указывающими направление прохождения сигнала. Считается, что в объекте может выходить из строя только один функциональный элемент. При этом i -е неисправное состояние идентифицируется с отказом i -го блока. В этой ситуации запись состояния s представляется в виде вектора S, в котором количество координат соответствует количеству блоков. Значения координат задаются в соответствии со следующими правилами: если блок исправен, то координата равна 1, а если блок неисправен, то координата равна 0. Например, если объект диагностики имеет пять блоков, то исправное состояние запишем вектором S ₀ (l1111), при неисправном первом блоке техническое состояние запишется следующим вектором S ₁ (01111).

Под проверкой p _j понимается операция по оценке выходных сигналов всех блоков объекта при нахождении его в состоянии s_i. При наличии в объекте диагностики n функциональных блоков общее количество технических состояний равно n + 1 (n неисправных и одно исправное), а количество проверок равно n.

При формальном описании результатов j -й проверки R_i^j отдельного элемента функциональной схемы при нахождении объекта в i -м состоянии принимаются следующее правила:

1. Результат принимается равным 1, если блок исправен и на его входы подаются допустимые воздействия.

2. Результат принимается равным 0, если на входы блока подаются допустимые воздействия, а он неисправен.

3. Результат принимается равным 0, если блок исправен, но хотя бы на один его вход подается недопустимое воздействие.

Пользуясь таким представлением, можно задать все множество технических состояний объекта, множество проверок, множество результатов и составить таблицу состояний.

Рассмотрим пример построения таблицы состояний объекта диагностики, который можно представить функциональной моделью, состоящей из шести элементов (рис. 3.2).

 

Рис. 3.2 Пример функциональной шестиэлементной модели

 

Для такой модели количество элементарных технических состояний равно семи. Исправное состояние можно представить шестимерным вектором S ₀ (111111), при отказе блока Q ₁ техническое состояние представим вектором S ₁ (011111) и т.д. Поскольку в объекте шесть блоков, то для проверки функционирования каждого блока необходимо проверить его выходной сигнал. Следовательно, количество необходимых проверок равно шести. Будем считать, что при проведении каждой из проверок
p _j (j = 1...6) на вход модели подаются входные воздействия x ₁ и х ₂, которые принимают только допустимые значения. В то же время выходные сигналы блоков y_i (i = 1...6) могут принимать как допустимые, так и недопустимые значения. Допустимое значение выходной сигнал принимает в случае, если блок исправен и на его входы подаются допустимые воздействия. Недопустимое значение выходной сигнал принимает в двух случаях: если блок исправен, но на его входы подаются недопустимые сигналы, или если входные сигналы принимают допустимые значения, но блок неисправен.

С учетом этого и пользуясь изложенными выше тремя правилами, результат элементарной проверки блоков объекта, находящегося в i -м техническом состоянии (отказ i -гo блока), будем принимать равным 1, если сигнал на выходе проверяемого блока принимает допустимое значение, и равным 0, если сигнал на выходе проверяемого блока принимает недопустимое значение. Например, при отказе блока Q ₂ нулевые значения примут результаты R ²₂, R ²₃, R ²₆, поскольку при проведении элементарных проверок p₂, p₃, p₆ для блоков Q ₂, Q ₃, Q ₆ выходные сигналы примут недопустимые значения. Воспользовавшись приведенными выше рассуждениями, составим таблицу 3.2 состояний для объекта, функциональная модель которого изображена на рисунке 3.2.

Таблица 3.2

Таблица состояний для шестиэлементного объекта

p \ s	S 0	S 1	S 2	S 3	S 4	S 5	S 6
p1
p2
p3
p4
p5
p6

 

Полученная таблица является как проверяющей, так и разделяющей, т.е. позволяет решать задачи контроля и диагностики.

Непременным условием применения функциональной модели является наличие у всех элементов (блоков) объекта диагностирования одного выхода. В реальных условиях выходной сигнал некоторых блоков объекта контроля может характеризоваться несколькими параметрами. В этом случае считается, что блок имеет несколько выходных сигналов, каждый их которых характеризует соответствующий параметр. В такой ситуации применяют так называемое «расщепление» выходов. Рассмотрим применение этого приема на примере.

На рисунке 3.3 изображена схема системы электроснабжения самолета.

 

Рис. 3.3 Схема системы электроснабжения

ППО – привод постоянных оборотов; СГС – синхронный генератор самолетный; РН – регулятор напряжения; РЧ – регулятор частоты; БЗУ – блок защиты и управления; П_дв – частота вращения коробки приводов двигателя; П_ППО – частота вращения генератора; U и f – напряжение и частота на выходе генератора; I _в – ток возбуждения генератора; I_f – управляющее воздействие по частоте на ППО; U – напряжение, подаваемое в самолетную сеть.

Выходной сигнал генератора характеризуется двумя параметрами: напряжением и частотой. При составлении функциональной модели проводится «расщепление» выходного сигнала генератора по следующим правилам.

Правило первое. Если выходной сигнал характеризуется несколькими параметрами, то выходной сигнал «расщепляется» на количество сигналов, равное количеству параметров.

Схема системы электроснабжения с «расщепленным» выходным сигналом генератора представлена на рисунке 3.4.

 

Рис. 3.4 Схема с «расщепленным» выходным сигналом генератора

 

В соответствии с этой схемой один из блоков (генератор) объекта диагностирования имеет два выхода, что не может быть в функциональной модели. Для приведения в соответствие количества выходов блоков с требованием функциональной модели пользуются вторым правилом.

Правило второе. Если i -й блок имеет несколько выходов, то на функциональной модели он заменяется несколькими блоками, имеющими только один выход. Число блоков равно числу выходов «расщепляемого» блока.

С учетом этого правила предыдущую схему представим следующим образом (рис. 3.5).

Рис. 3.5 Схема с «расщепленным» выходом генератора

 

Приведенная схема соответствует требованиям функциональной модели, что позволяет изобразить модель в принятых ранее обозначениях (рис. 3.6).

 

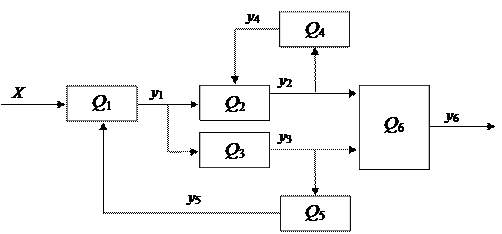
Рис. 3.6 Функциональная модель системы электроснабжения самолета

 

Пользуясь этой моделью, можно составить таблицу состояний (таблица 3.3). Таблица состояний заполняется исходя из следующих соображений. При исправном состоянии всех блоков сигналы на их выходах будут принимать допустимые значения, т.е. результаты всех проверок будут равны 1. При отказе первого блока на выходе всех блоков сигналы будут принимать недопустимые значения, т.е. результаты всех проверок будут равны 0. При отказе блока № 2 недопустимые значения выходных сигналов будут у блоков № 2, № 4 и № 6, т.е. результаты проверок этих блоков будут равны 0. Для остальных блоков результаты проверок будут равны 1. На основе подобных рассуждений заполняется вся таблица.

Таблица 3.3

Таблица состояний системы электроснабжения

p \ S	S 0	S 1	S 2	S 3	S 4	S 5	S 6
p1
p2
p3
p4
p5
p6

 

Представленная таблица является проверяющей, т.е. она решает только задачу контроля. Для технических состояний S ₁, S ₃, S ₅, а также для состояний S ₂, S ₄ результаты элементарных проверок совпадают. Следовательно, для выбранного набора проверок эти состояния неразличимы между собой.

Для того, чтобы исправить это положение, необходимо изменить структуру модели и элементарных проверок. Изменение структуры обеспечим путем разрыва обратных связей между блоками Q ₄ и Q ₂, а также между блоками Q ₅ и Q ₁. Структуру проверок изменим путем введения дополнительных внешних воздействий х ₄ и х ₅, которые будут подаваться на входы блоков, соответственно, Q ₂ и Q ₁ вместо выходных сигналов у ₄ и у ₅ от блоков Q ₄ и Q ₅. При таких заменах модель будет выглядеть следующим образом (рис. 3.7).

 

Рис. 3.7 Функциональная модель системы электроснабжения
с разорванными обратными связями

 

При выполнении всех проверок будем считать: входные воздействия х, х ₄ и х ₅ принимают только допустимые значения. Проведя те же рассуждения, что и при построении таблицы 3.3, получим несколько другую таблицу (таблица 3.4).

Таблица 3.4

Таблица состояния системы электроснабжения
с разорванными обратными связями

p \ S	S 0	S 1	S 2	S 3	S 4	S 5	S 6
p1
p2
p3
p4
p5
p6

 

Представленная таблица становится различающей и позволяет решать задачи диагностики. На практике задачу изменения структуры объекта диагностирования путем разрыва обратных связей и подачи на вход проверяемых блоков допустимых воздействий можно решить, например, применяя специальные средства диагностики.

Таким образом, можно сделать следующее важное замечание: если в функциональной диагностической модели (схеме) имеются обратные связи, охватывающие несколько блоков, то в таблице состояний отказы этих блоков неразличимы. Различие отказов этих блоков возможно только при изменении структуры объекта или при введении дополнительных проверок.

В некоторых случаях при выполнении дополнительных проверок для формирования признаков состояния можно использовать различные уровни выходных параметров проверяемых блоков. Так, для выходного напряжения генератора можно сформулировать два признака:

– напряжение генератора находится в пределах допуска:

® u _min £ у ₂ £ u _max;

– на выходе генератора отсутствует перенапряжение:

® у ₂ £ u _max.доп.

Если на выходе генератора наблюдается большая величина выходного напряжения, т.е. выходной параметр принимает недопустимое значение, то это является признаком отказа регулятора напряжения, ведущего к значительному увеличению тока возбуждения генератора и, как следствие, к перенапряжению на выходе генератора.

Функциональную модель применяют тогда, когда объект состоит из ярко выраженных функциональных блоков. В тех случаях, когда объект диагноза не имеет явно выраженных блоков, построение функциональной модели может оказаться невозможным.

В реальных условиях существуют объекты, для которых аналитические и другие виды зависимостей между параметрами технического состояния и диагностическими параметрами неизвестны, а известно только, что один параметр влияет на другой. Т.е. имеется информация о том, что существуют причинно-следственные связи между параметрами, событиями или явлениями. В таких ситуациях построение таблицы состояний возможно на основе построения и анализа графа причинно-следственных связей.

3.3 Модели на основе графов
причинно-следственных связей

 

Графом причинно-следственных связей называется ориентированный граф, вершины которого отображают собой параметры, события или явления, а дуги, соединяющие эти вершины, отражают причинно-следственные связи между соответствующими параметрами, событиями или явлениями. Стрелки на дугах направлены от причины к следствию.

С помощью графа причинно-следственных связей можно анализировать и объекты, представленные в виде функциональных моделей. В этом случае граф будет иметь вершины, которые соответствуют входным параметрам модели и выходным параметрам блоков модели. Дуги графов будут соответствовать связям между блоками, а также между входными параметрами и блоками модели.

В качестве примера построим граф причинно-следственных связей для функциональной модели, изображенной на рисунке 3.2. В вершинах графа (рис. 3.8) в данном случае помещают входные параметры х ₁ и х ₂ системы и выходные параметры блоков у_i (i = 1...6).

 

Рис. 3.8 Граф причинно-следственных связей для шестиэлементной модели

Вершины с параметрами х ₁ и х ₂ называются начальными или корневыми вершинами графа. Вершины с параметрами у ₃ и у ₆ называются висячими вершинами графа.

Данный пример показывает, что граф более конкретно отражает связь между параметрами, событиями или явлениями, помещенными в вершины графа. По нему четко видно, что если параметр в вершине графа принимает недопустимое значение, то такое же недопустимое значение принимает параметр, связанный с ним причинно-следственной связью (дугой).

Используя полученный граф, можно производить все те же операции, что и по функциональной модели: строить таблицу состояний; выбирать набор проверок (признаков) для проверяющей и различающей совокупностей. Рассмотренный пример является частным, поскольку в вершинах графа находятся измеряемые параметры. Возможности графов намного шире, они определяются тремя основными положениями:

1. Путем построения графов причинно-следственных связей можно устанавливать зависимости не только между параметрами, но и между событиями, которые определены логическими высказываниями.

Например, «Значение параметра (предположим T_Г *) не выходит за пределы заданной для него области допустимых значений». Такие события можно помещать в вершины графа и дугами устанавливать между ними связи. Если истинность этого высказывания (т.е. нахождения параметра в норме) условиться представлять единицей, то ложность этого события (т.е. выход параметра за допуск) можно представлять нулем. Такое описание истинного и ложного событий совпадает с тем описанием, которое было принято раньше для функциональных моделей. Это и является предпосылкой для построения на основе графа причинно-следственных связей таблицы состояний.

2. При построении графа причинно-следственных связей можно в вершины графов проставлять не все входные, внутренние и выходные параметры (события или явления), которые происходят в объекте, а только те из них, которые доступны для измерения или регистрации.

3. Для функциональных моделей принято, что неисправностью объекта является любая неисправность, приводящая к появлению недопустимого значения параметра на выходе одного из блоков. Количество неисправностей системы совпадает с количеством имеющихся блоков. При построении графа причинно-следственных связей количество диагностируемых состояний (дефектов) можно искусственно уменьшить путем задания конкретного перечня неисправностей, которые требуется обнаружить. Такое задание неисправностей в виде списка равносильно тому, что неисправности, не внесенные в список, маловероятны или невозможны. Уменьшение числа неисправностей при решении практической диагностической задачи уменьшает число параметров, подлежащих измерению и, как следствие, уменьшает объемы проверяющей и особенно различающей совокупностей.

В качестве примера, иллюстрирующего особенности применения графов для задач диагностики, рассмотрим построение таблицы состояния с использованием графа причинно-следственных связей для системы смазки редуктора, схема которой изображена на рисунке 3.9.

 

Рис. 3.9 Схема системы смазки редуктора

 

Будем считать, что выходными параметрами, характеризующими техническое состояние всего редуктора, являются величины температур трех основных подшипников редуктора Т ₁, Т ₂, Т ₃ Смазка редуктора (в том числе и подшипников) осуществляется маслом, циркуляция которого обеспечивается шестеренчатым насосом, который имеет нагнетающую (НС) и откачивающую (ОС) секции и создает в напорной магистрали давление Р _н. Стабилизацию температуры масла в баке Т _б обеспечивают прокачкой масла через радиатор. Расход масла через радиатор зависит от положения перепускного клапана. Если клапан закрыт (обозначим это событие К ₃), то все масло при откачке проходит через радиатор и температура масла в баке падает. Если клапан открыт (обозначим это событие К _о), то происходит увеличение температуры масла в баке. Кроме температуры масла будем контролировать и его уровень в баке Y _б.

Для определения вершин графа составим список недопустимых событий для данной системы:

1. Превышение температуры подшипников предельно допустимого значения Н, т.е. Т ₁ > Н; Т ₂ > Н; Т ₃ > Н.

2. Давление масла в нагнетающей магистрали ниже нормы Н₁, т.е. Р _н < Н₁.

3. Уровень масла в баке ниже минимально допустимого Н₂, т.е. Y _б < Н₂.

4. Температура масла в баке выше максимально допустимой Н₃, т.е. Т _б > Н₃.

5. Температура масла в баке ниже минимально допустимой Н₄, т.е. Т _б < Н₄.

6. Перепускной клапан постоянно закрыт, т.е. имеется событие К ₃.

7. Перепускной клапан постоянно открыт, т.е. имеется событие К_о. Перечисленные события определяют вершины графа. Для устан

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: