 |
Определение количества информации
|
|
|
|
С точки зрения диагностики, важно определять не саму энтропию системы, а то количество информации, которое приобретается о состоянии системы в результате измерения некоторого комплекса (набора, вектора) признаков.
Рассмотрим следующий пример. Пусть объектом диагностики является маслосистема, которая может находиться либо в исправном А 1, либо в неисправном А 2 состояниях. Для диагностирования системы проводятся измерение температуры t м или давления Р м масла.
Очевидно, что до выполнения измерений дать ответ о состоянии системы весьма затруднительно. Можно предположить, что исправное и неисправное состояния являются равновероятными, т.е. Р (А 1) = Р (А 2) = 0,5. Таким образом, с учетом изложенного выше, можно определить начальную энтропию системы до проведения измерений Н нач(А), которая равна
.
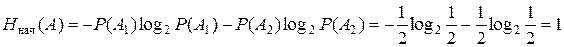Пусть для температуры предельное значение составляет 90°С. Из опыта эксплуатации установлено, что при температуре масла t м < 90°C в 60% случаев масляная система находится в исправном состоянии, т.е. при t м < 90°С Р (А 1) = 0,6, а Р (А 2) = 0,4. Следовательно, если в процессе измерения установлено, что температура масла меньше 90°С, то энтропия системы равна
.
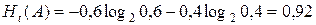Количество информации о состоянии системы А, которое мы получили по результатам измерения температуры IA (t м), определим как разность начальной энтропии H нач(а) и значения энтропии, которую имела система после измерения температуры Нt (А):
I a(t м)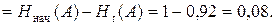 
Для этой же системы известно, что если давление масла в системе превышает две атмосферы, то вероятность нахождения системы в исправном состоянии равна единице, а в неисправном – нулю, т.е. при Р м > 2 атм P (A 1) = 1, а Р (А 2) = 0. Поэтому если в процессе измерения установлено, что давление масла в системе превышает две атмосферы, то энтропия системы равна
|
|
|
НР (А) = –1 log21 – 0 log2 0 = 0.
Как и в предыдущем случае, количество информации о состоянии системы А, которое мы получили по результатам измерения давления IА (Р м), определим как разность начальной энтропии H нач(A) и значения энтропии, которую имела система после измерения давления H Р(А):
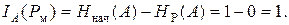
В общем случае задача определения количества информации ставится таким образом. Пусть имеется система (объект диагностики) А, которая может находиться в одном из состояний Ai (где i = 1... N). В каждом из этих состояний объект может находиться с определенной вероятностью P (Ai). С этим объектом связан комплекс (система, вектор) диагностических признаков К. Этот комплекс (вектор) задается своими компонентами (координатами), число которых равно n. Другими словами, объект диагностики описывается в n -мерном пространстве диагностических признаков. В процессе диагностирования, после проведения соответствующих измерений и обработки диагностических параметров, определяются конкретные значения (реализации) диагностических признаков по всем n координатам. В свою очередь, этот комплекс, состоящий из n реализаций диагностических признаков, определяет некоторую j -ю реализацию вектора диагностических признаков Kj, принадлежащую множеству К. Математически эти рассуждения можно записать следующим образом:
,
где К * – экспериментально полученная реализация вектора диагностических признаков К; Kj – экспериментально полученная конкретная j -я реализация вектора диагностических признаков; Кjs – экспериментально полученная реализация диагностического признака по s -й координате, соответствующая j -й реализации вектора диагностических признаков Кj; s = 1,..., n; j = 1,..., m.
В диагностическом смысле задача оценки количества информации формулируется так: необходимо определить количество информации, которое получается о состоянии системы А, после измерения всех реализаций вектора диагностических признаков, входящих во множество К. В такой постановке количество информации записывается следующим образом:
|
|
|
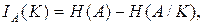(4.2)
где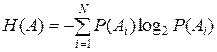 
– начальная энтропия объекта диагностики, которая определяется по априорным данным; Н (А / К) – энтропия системы А после того, как стали известны все реализации вектора диагностических признаков из множества К.
Вычисление начальной энтропии при известных вероятностях Р (Аi) не вызывает затруднений. Рассмотрим второй член в правой части выражения (4.2), который называется условной энтропией. Эта условная энтропия вычисляется таким же образом, как и начальная энтропия, только вместо вероятности появления события Аi подставляется условная вероятность нахождения системы в состоянии Аi при наблюдении всех реализаций вектора признаков Kj из множества К, т.е.
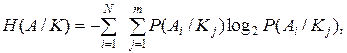
где Р (Ai / Kj) – условная вероятность нахождения объекта диагностирования в состоянии Аi при условии, что вектор диагностических параметров получит реализацию Kj; i = 1... N – номер технического состояния (диагноза); j = 1... m – номер реализации вектора диагностических признаков.
После подстановки начальной и условной энтропии в выражение (4.2) и соответствующих преобразований выражение для количества информации, получаемого при обследовании всех диагнозов Аi по всем реализациям вектора диагностических признаков Kj, будет иметь вид
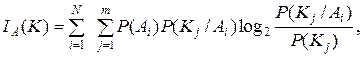(4.3)
где P (Kj / Ai) – условная вероятность появления j -й реализации вектора признаков Кj при нахождении системы в Аi состоянии; Р (Кj) – вероятность появления j -й реализации вектора признаков Кj при нахождении объекта диагностики во всех возможных состояниях.
Используя известные из теории вероятностей соотношения между вероятностями совместного появления событий и условными вероятностями появления событий:
,
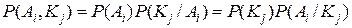выражение (4.3) для количества информации можно представить в другом виде:
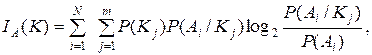(4.4)
или
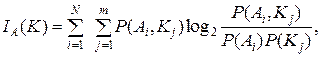(4.5)
где Р (Ai / Kj) – вероятность нахождения объекта в диагнозе Аi при условии, что в ходе процесса диагностирования была получена реализация вектора диагностических признаков Кj; P (Ai, Kj) – вероятность совместного появления следующих событий: нахождение объекта в диагнозе Аi и получение в процессе диагностирования реализации диагностических признаков Кj.
|
|
|
При анализе выражения (4.5) можно сделать вывод, способствующий физическому пониманию расчетных формул, предназначенных для оценки величины получаемой информации. Так, если система признаков выбрана неправильно, то она оказывается не связана с техническим состоянием. Говоря по-другому, все диагнозы объекта и все реализации векторов диагностических признаков являются независимыми событиями, т.е. P (Ai, Kj) = P (Ai) P (Kj). Тогда, как следует из выражения (4.5), IA (K) = 0. Следовательно, в такой ситуации знание диагностических признаков не дает никакой информации о техническом состоянии объекта диагностики.
При необходимости определить количество информации, получаемое об отдельном состоянии Аi при обследовании по всем реализациям вектора признаков Kj, в предыдущих выражениях необходимо опустить суммирование по i (i = 1... N). Тогда мы получим три выражения для определения IАi (K):
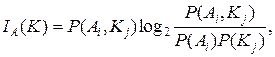(4.6)
или
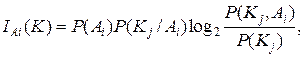(4.7)
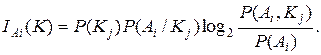(4.8)
Если необходимо определить количество информации IАi (Кj), которое получают о состоянии системы Ai при измерении в процессе диагностирования конкретной реализации вектора диагностических признаков Кj, то в предыдущих выражениях надо вообще опустить суммирование:
(4.9)
или
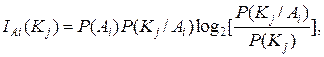(4.10)
или
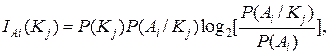(4.11)
Итак, последние выражения для IAi (Kj) определяют ожидаемое количество информации о состоянии Ai, получаемое при появлении в ходе процесса диагностирования конкретной реализации вектора диагностических признаков Кj.
В общей постановке вектор диагностических признаков может содержать любое число компонент, т.е. объект диагностирования может быть определен в пространстве диагностических признаков любой размерности. Следовательно, количество диагностических признаков, являющихся компонентами вектора, может изменяться от одного до бесконечности. Поэтому полученные выражения могут быть применены и к случаю, когда вектор диагностических признаков содержит только один компонент, т.е. Kj = kj. Тогда, если в выражениях (4.9), (4.10) и (4.11) заменить Kj на kj, то они будут определять количество информации, получаемое о состоянии Аj при обследовании по конкретному признаку kj.
|
|
|
|
|
|
