Методы оптимизации диагностических тестов

 

Таблица состояний является удобной формой задания оператором объекта диагностирования. Однако она может содержать избыточное количество проверок, в которых используется большое количество признаков. Поэтому возникает задача выбора минимального количества проверок и признаков, достаточных для решения задач контроля и диагностики.

Пусть в результате анализа объекта диагностирования была составлена функциональная модель и заполнена таблица состояний (таблица 3.6).

Таблица 3.6

Таблица состояний с избыточным числом проверок

p \ S	S 0	S 1	S 2	S 3	S 4	S 5	S 6	S 7
p1
p2
p3
p4
p5
p6
p7
p8
p9
p10
p11
p12

 

Отсутствие одинаковых столбцов в таблице свидетельствует о том, что выбранный набор элементарных проверок (признаков) позволяет различать все восемь состояний, т.е. таблица является проверяющей и различающей. Однако этот набор проверок является избыточным и необходимо провести оптимизацию их количества. Оптимизация тестов и выбор минимального количества проверок (признаков) осуществляется в несколько этапов.

Первый этап

Выполняется оценка проверок (признаков) на их информативность. На этом этапе отбрасываются те признаки или проверки, которые в строке имеют все нули или все единицы. Т.е. отбрасываются проверки (признаки), которые не различают состояния, занесенные в таблицу. В нашей таблице такой проверкой является проверка p₁₂.

Второй этап

Просматриваются все проверки (признаки) на предмет их тождественности отображения состояния, т.е. просматривается таблица на предмет наличия одинаковых строк. Из тождественных признаков выбираются, как правило, те, которые проще всего измерить. В нашей таблице одинаковые строки соответствуют проверкам p₁ и p₁₀, а также p₈ и p₁₁. Следовательно, из представленного в таблице комплекса проверок следует исключить проверки p₁₀, p₁₁, p₁₂, как неинформативные.

Полученная в результате таблица также является проверяющей и различающей. Однако и эта совокупность проверок все еще остается избыточной. Если бы объект контроля был идеально приспособлен для диагностики, то минимальное число проверок J, необходимое для распознавания N состояний, определялось соотношением J = log₂ N. В нашем случае для разделения восьми технических состояний выполняется девять проверок, что явно не соответствует этому соотношению. Поэтому проводится третий этап оптимизации, который может выполняться различными методами [15, 16, 20].

Наиболее часто используют метод определения минимального набора проверок (признаков) с помощью общей различающей логической функции и табличный метод минимизации теста по максимальному числу вхождений проверок в различающую функцию.

Первый метод является математически строгим, позволяет выбрать оптимальный тест, но он достаточно трудоемок. Поэтому рассмотрим более простой и наглядный табличный метод.

Табличный метод минимизации теста по максимальному числу
вхождений проверок в различающую функцию

Перепишем таблицу 3.6, исключив из нее неинформативные проверки p₁₀, p₁₁, p₁₂. Полученная в результате исключения этих проверок таблица представлена ниже (таблица 3.7).

Таблица 3.7

Таблица состояний с избыточным числом проверок

p \ S	S 0	S 1	S 2	S 3	S 4	S 5	S 6	S 7	W
p1
p2
p3
p4
p5
p6
p7
p8
p9

 

Пусть в j -й строке результаты проверки p _j примут значение, равное единице, m_j раз, а значение, равное нулю, n_j раз.

Под числом вхождений проверок (признаков) данной строки W_j понимают произведение количества нулей на количество единиц:

W_j = m_jn_j. (3.6)

В последнем столбце таблицы 3.7 приведены значения числа вхождений, подсчитанные для соответствующих проверок (строк). Максимальное число W = 16 для трех проверок π₅, π₇, π₈. В тест следует выбрать одну из этих проверок. Выбирается тот признак или проверка, которые проще измерить. Например, возьмем проверку под номером пять.

Далее таблица перестраивается таким образом, чтобы она разделялась на две части. В левой половине этой таблицы собираются все состояния, у которых результат пятой проверки равен единице (S ₀, S ₅, S ₆, S ₇), а в правой половине все состояния, для которых результат равен нулю (S ₁, S ₂, S ₃, S ₄) (таблица 3.8).

Таблица 3.8

p \ S	I = 1	I = 2
S 0	S 5	S 6	S 7	S 1	S 2	S 3	S 4	W
p5
p1									0 + 3 = 3
p2									3 + 3 = 6
p3									0 + 3 = 3
p4									3 + 0 = 3
p6									3 + 4 = 7
p7									4 + 4 = 8
p8									3 + 3 = 6
p9									3 + 3 = 6

 

На втором шаге также считается количество вхождений для каждой проверки (строки) как сумма вхождений проверок, подсчитанных для первой и второй половин таблицы 3.8:

W = (n_jm_j)₁ + (n_jm_j)₂. (3.7)

Полученные значения приведены в последнем столбце таблицы 3.8. Максимальное значение числа вхождений имеет проверка под номером семь p₇. Перестроим таблицу 3.8 по p₇ таким образом, чтобы новая таблица 3.9 делилась на четыре части и чтобы в каждой из новых частей были собраны состояния, где p₇ равна только единице или только нулю.

Таблица 3.9

p \ S	I = 1	I = 2	I = 3	I = 4
S 0	S 5	S 6	S 7	S 3	S 4	S 1	S 2	W
p5
p7
p1
p2
p3
p4
p6
p8
p9

 

На третьем шаге количество вхождений для каждой проверки определяется как сумма вхождений, подсчитанных для каждой из четырех частей таблицы:

W = (n_jm_j)₁ + (n_jm_j)₂ + (n_jm_j)₃ + (n_jm_j)₄. (3.8)

Максимальное число вхождений имеет проверка p₆. В результате проверки p₅, p₇, p₆ не различают только два состояния S ₆ и S ₇. Из приведенных таблиц следует, что для их разделения необходимо выполнить проверку p₂. Таким образом, мы получаем минимальный тест для разделения восьми технических состояний, в которых может находиться объект, представленный в таблице 3.6. В этот тест следует ввести проверки p₅, p₇, p₆ и p₂. При этом исходную таблицу 3.6 следует преобразовать к окончательному виду (таблица 3.10).

Таблица 3.10

p \ S	S 0	S 1	S 2	S 3	S 4	S 5	S 6	S 7
p2
p5
p6
p7

 

Из всего вышеизложенного можно построить дерево алгоритма определения технического состояния объекта диагностики, представленного в таблицах 3.6, 3.10 (рис. 3.12).

Рис. 3.12 Алгоритм определения состояния объекта

 

И функциональная модель, и граф причинно-следственных связей, в конечном итоге, определяют математическую модель объекта в виде таблицы состояний. Задание оператора объекта диагностирования в табличной форме достаточно удобно. Однако в ряде случаев (например, когда параметры определены на непрерывном множестве) такое представление оператора невозможно. В таких ситуациях математическая модель может быть представлена в виде аналитических зависимостей между входными возмущениями, параметрами технического состояния и диагностическими параметрами.

В технической диагностике математические (диагностические) модели объектов, устанавливающие связь между входными возмущениями, параметрами технического состояния и диагностическими параметрами (признаками) в виде аналитических зависимостей (уравнений) называются аналитическими моделями. Эти аналитические модели (зависимости) чаще всего могут быть представлены в виде алгебраических или дифференциальных уравнений. Познакомимся с некоторыми подобными моделями.

 

3.5 Аналитические модели в виде
дифференциальных уравнений

 

Наиболее часто аналитические модели в виде дифференциальных уравнений применяются в вибрационной диагностике. Это связано с тем, что вибрация (упругие механические колебания) механизмов – это их реакция на действие приложенных возмущающих сил, а основным математическим аппаратом для анализа вибрации (упругих механических колебаний) технических устройств является аппарат дифференциальных уравнений [1, 4, 7].

Вибрационное (колебательное) поведение технических систем описывается дифференциальным уравнением (системой уравнений), у которого (как правило) в правой части находится аналитическое выражение, определяющее зависимость возмущающих сил от времени. В левую часть этого уравнения (системы уравнений) помещены производные по времени перемещений точек механизма с коэффициентами, характеризующими инерционные (массовые), упругие (жесткостные) и демпфирующие (рассеивающие) свойства этого механизма. Отсюда следует, что анализ виброакустических процессов для целей диагностики позволяет выявить такие неисправности, которые приводят к изменению действующих на механизм возмущающих сил или к изменению инерционных, жесткостных и демпфирующих свойств этого механизма (например, разбалансировку роторов, нарушение соосности роторов, возникновение трещин, неисправности подшипниковых узлов и т.п.). Поясним это на простейшем примере.

Представим диагностируемый механизм в виде простой одномассовой колебательной системы (рис. 3.13), где F (t) – возмущающая внешняя сила; M – масса системы; C – коэффициент жесткости системы; H – коэффициент демпфирования в системе; X (t) – перемещение центра масс под действием возмущающей силы.

 

Рис. 3.13 Простейшая одномассовая колебательная система

Колебания центра масс этой системы описываются следующим дифференциальным уравнением:

. (3.9)

Общее решение этого уравнения, описывающее зависимость перемещения центра масс от времени, записывается в следующем виде:

, (3.10)

где х _св(t) определяет свободные колебания центра масс, a x _b(t) – вынужденные.

Для того, чтобы в ходе решения уравнения (3.9) получить конкретные аналитические зависимости от времени свободных и вынужденных колебаний, необходимо определить в конкретном аналитическом виде зависимость от времени возмущающей силы [5, 14]. Представляя сами колебания и действие сил в виде ряда Фурье, примем, что возмущающая сила, действующая на систему, является гармонической, т.е. F (t) = F ₀ sin(w t), где F ₀ – амплитуда возмущающей силы; w – частота возмущающей силы. С учетом этого выражение (3.9) можно переписать в виде

. (3.11)

Решая это уравнение, получим, что свободные колебания являются затухающими и определяются выражением

, (3.12)

где 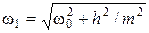– частота свободных колебаний; – собственная частота колебаний системы.

Необходимо отметить, что в реальных системах m >> h, поэтому свободные колебания механических систем совершаются с частотой, практически равной собственной частоте системы (т.е. w₁» w₀). Воспроизвести свободные колебания в реальных условиях можно путем тестового воздействия на объект коротким импульсом возмущающей силы, т.е. ударом.

При возбуждении системы (см. рис. 3.13) ударом она будет совершать свободные колебания с частотой, равной собственной частоте системы. Амплитуда колебаний будет зависеть от соотношения между амплитудой силы и жесткостью системы. Скорость затухания колебаний будет определяться величиной соотношения демпфирования и массы в системе. Отсюда следует, что обнаружить неисправность объекта путем анализа его свободных колебаний можно в том случае, если эта неисправность вызовет изменение частоты свободных колебаний или скорости их затухания, т.е. если неисправность повлияет на динамические (жесткостные, демпфирующие, массовые) характеристики системы.

Если поведение системы описывается уравнением (3.11) и на нее постоянно действует гармоническая сила, то через определенный интервал времени свободные колебания затухнут, и система будет совершать только вынужденные колебания. Эти колебания будут также гармоническими, а их аналитическая зависимость определяется выражением

(3.13)

где Х ₀ – амплитуда вынужденных колебаний; w – частота вынужденных колебаний.

Частота вынужденных колебаний равна частоте возбуждающей силы, а амплитуда колебаний зависит от амплитуды возбуждающей силы и коэффициента динамичности b:

. (3.14)

Коэффициент динамичности зависит только от характеристик системы и для нашего случая определяется следующим соотношением:

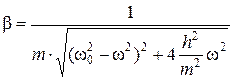. (3.15)

Максимальное значение коэффициент динамичности принимает при равенстве частоты возбуждающей силы собственной частоте системы: w = w₀. Такое явление называется резонансом, и говорят, что система совершает резонансные колебания. Как следует из соотношения (3.15), амплитуда резонансных колебаний зависит от величины возбуждающей силы и демпфирующих свойств системы.

Приведенные соотношения свидетельствуют о том, что диагностика объектов путем анализа вынужденных колебаний возможна в том случае, если неисправности вызывают изменение возбуждающей силы (ее величины или частоты) или изменение динамических свойств самого объекта (массы, жесткости, демпфирования).

Представленные выше зависимости выходного сигнала (колебаний) описывают только одно техническое состояние механизма (исправное), для получения описаний неисправных состояний необходимо установить зависимости между параметрами силы (входным воздействием) и дефектами или зависимости между массой, жесткостью, демпфированием и дефектами, т.е. для вибрационной диагностики характерно задание неявных моделей.

Реальные механизмы обладают бесконечным числом собственных форм и частот колебаний, для их диагностирования по вибрационным параметрам на практике можно применить следующий прием [7]. Для каждой собственной формы и частоты колебаний реального механизма устанавливается соответствие с гипотетической одномассовой системой, и реальный механизм рассматривается как набор одномассовых систем. Любые механизмы с определенными допущениями можно представить набором одномассовых систем. Сложное входное возмущение можно представить в виде ряда Фурье, что позволяет анализировать реакцию механизма на отдельное гармоническое возмущение.

При таком подходе основная задача – это правильно определить основные (определяющие) собственные формы и частоты диагностируемого механизма. Исправное техническое состояние будет описываться характерными только для исправного объекта амплитудно-частотным составом возмущающей силы и динамическими свойствами (инерционными, жесткостными, демпфирующими) выбранных определяющих форм колебаний. Для задания неисправных технических состояний необходимо установить зависимости амплитудно-частотного состава возмущающей силы и динамических свойств определяющих форм колебаний от конкретных неисправностей механизма.

При более общем подходе реальную механическую (колебательную) систему можно представить как многомерную систему с m входами и n выходами (рис. 3.14), где F_j – внешняя возмущающая сила, действующая на j- й вход системы; X_i – перемещение механической системы на i -м выходе.

 

Рис. 3.14 Упрощенное представление диагностируемого объекта
в виде многомерной колебательной системы

В этом случае оператор А представляет собой систему дифференциальных уравнений с n степенями свободы.

[M]· [X″] + [H] ·[X′] + [C] ·[X] = [F]. (3.16)

Если система имеет n уравнений, то симметричные матрицы [M], [H], [C]имеют размерность и описывают соответствующие инерционные, демпфирующие и жесткостные свойства системы, а векторы [X] и [F] имеют размерность n и описывают координаты системы и возмущающие силы. Отметим, что и в этом случае диагностическая модель является неявной, что характерно для задач вибрационной диагностики.

Рассмотрим в качестве примера, как изменятся вибрационные характеристики стержня или пластины, которыми можно смоделировать вал или лопатку, при появлении трещины. Представим себе балку на шарнирных опорах или с защемленным концом, у которой появилась трещина (рис. 3.15).

 

Рис. 3.15 Схема балки с трещиной

 

Будем считать, что балка совершает колебания по первой (определяющей) форме, которая на рисунке изображена пунктирной линией. При колебаниях «берега» трещины будут то сжиматься (при сжатии), то разжиматься (при растяжении). Очевидно, что при сжатии материал ведет себя как сплошной. При растяжении, поскольку «берега» трещины раскрываются, жесткость балки уменьшается, т.к. трещина не работает на растяжение. Таким образом, изделие с трещиной имеет различные жесткости в направлениях сжатия и растяжения. Ранее отмечалось, что жесткость определяет динамические свойства (собственную частоту) системы. Следовательно, у изделия с трещиной изменится собственная частота системы, поскольку она определяется соотношением жесткости и массы (см. (3.16)).

Так как мы рассматриваем колебания балки по первой (определяющей) форме колебаний, то смоделируем ее одномассовой системой с соответствующими параметрами (собственная частота системы должна быть равна собственной частоте исследуемой балки). Для упрощения рассмотрения не будем учитывать демпфирование в системе. Одномассовая система, моделирующая балку без трещины при принятых допущениях, представлена на рисунке 3.16. Свободные колебания этой системы описываются дифференциальным уравнением следующего вида: mх ″ + Сх = 0, которое преобразуется в выражение

(3.17)

где w₀ = – собственная частота системы.

 

Рис. 3.16 Жесткость системы без трещины

 

Определим начальные условия для момента времени t = 0. Будем считать, что для начального момента времени координата центра тяжести массы равна нулю (х = 0), а его скорость имеет конечное значение V ₀ (x '= V ₀). Уравнение свободных колебаний без демпфирования при наличии в начальный момент скорости определяется следующим уравнением:

. (3.18)

Из этого уравнения следует, что при отсутствии трещины свободные колебания совершаются с частотой, равной собственной частоте системы.

Изменим систему, изображенную на рисунке 3.16, таким образом, чтобы она отражала изменение динамических характеристик при появлении трещины. Наличие трещины учтем добавочной пружиной С _доб
(рис. 3.17). С _доб – жесткость, которая учитывается только при сжатии
(при х < 0); С ₀ – жесткость неповрежденного участка; С _доб – жесткость вала, которая добавляется при закрытии трещины.

 

Рис. 3.17 Жесткость системы, имитирующей трещину

 

Жесткость С ₀ работает и на растяжение, и на сжатие. Она моделирует жесткость неповрежденного участка вала. В первом приближении можно считать, что отношение добавочной жесткости к основной жесткости равно отношению длины трещины _тркхарактерному размеру изделия (например, лопатки) _лоп в направлении трещины: 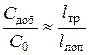. Следовательно, в реальной ситуации С _доб << С ₀. Введем следующие обозначения:

; ; С = С ₀ + С _доб; .

В силу С _доб << С ₀ имеем w» w_осн.

С учетом принятых обозначений и допущений свободные колебания системы, изображенной на рисунке 3.17, будут описываться следующими уравнениями:

(3.19)

При задании начальных условий t = 0; х = 0; х ' = V ₀ можно получить решение этих уравнений. Решение будет периодической функцией с периодом Т» p/w. Время будет изменяться в интервале от p/w до p/w_ОСН. Решение дифференциальных уравнений (3.19) в указанном временном интервале будет иметь следующий вид:

(3.20)

Функция, заданная уравнениями (3.20), несимметрична относительно начала координат. Справа и слева от начала координат несколько отличаются амплитуды и частоты колебаний. Применим к функции x (t)разложение в ряд Фурье, что позволит представить ее в виде суммы отдельных гармонических составляющих:

,

где , коэффициенты ряда Фурье a_i и b_i определяются известными соотношениями:

Из анализа последних трех выражений следует, что свободные колебания системы, изображенной на рисунке 3.17, не являются гармоническими и содержат несколько составляющих. Например, для значения i = 1 будем иметь a ₁ = 0, b ₁ = V ₀/w. Для значения i = 2, соответственно, получим следующие значения:

а ₂ = 0; b ₂ = .

Отсюда отношение амплитуд второй и первой гармонических составляющих будет выражаться следующим уравнением:

Обобщая полученные результаты, можно сделать следующие выводы:

1. При появлении трещины свободные колебания системы становятся негармоническими, в сигнале присутствуют высшие гармоники, в частности вторая гармоника.

2. Отношение амплитуды второй (верхней) гармоники к амплитуде первой (основной) гармоники равно 1/3 отношения размера трещины к характерному размеру изделия.

3. Основная частота свободных колебаний изделия с трещиной меньше частоты свободных колебаний изделия без трещины, поскольку w₀ < w_осн.

В заключение следует отметить, что аналитические модели в виде дифференциальных уравнений применяются не только в вибрационной диагностике. Они используются также, например, в методах диагностирования по температурным полям.

Кроме дифференциальных уравнений аналитические модели могут быть представлены алгебраическими уравнениями.

 

3.6 Аналитические модели на основе
алгебраических уравнений

 

Если связь между входным возмущением, внутренними параметрами объекта диагностирования и выходными диагностическими параметрами представлена в виде алгебраического уравнения или системы алгебраических уравнений, то мы имеем аналитическую модель алгебраического вида. В зависимости от физического характера объекта диагностирования алгебраические уравнения могут быть линейными или нелинейными. В простейшем случае при описании объекта диагностики подобными моделями задается система линейных алгебраических уравнений, в которых количество уравнений равно числу неизвестных параметров технического состояния или числу диагнозов (т.е. числу выбранных для диагноза технических состояний).

Рассмотрим случай представления моделей в виде системы линейных алгебраических уравнений. В общем виде

. (3.21)

В этом уравнении X, Z, Y, соответственно, вектор входных возмущений, действующих на объект, вектор внутренних параметров объекта, вектор выходных диагностических параметров. Матрицы А, В, С являются матрицами коэффициентов уравнения.

При проведении диагностирования, как правило, располагают значениями диагностических параметров (т.е. известен вектор [Y]), по которому необходимо определить значения входных или внутренних параметров (т.е. определить векторы [X] или [Z]). С точки зрения математического решения задачи диагностики, между векторами входных параметров [X] и вектором внутренних параметров [Z] нет различия. Поэтому векторы [X] и [Z] можно объединить в общий вектор [R], который называется вектором влияющих факторов, и тогда уравнение (3.21) примет вид

. (3.22)

Вектор [Y] с компонентами y_i называют еще вектором отклика системы на вектор возмущающих факторов [R] с компонентами r_j.

Большинство линейных моделей, приведенных к окончательному виду, разрешены относительно выходных диагностических параметров (откликов) и описываются системой уравнений вида (3.20). Каждое отдельное уравнение в этой системе представляет собой зависимость одного отклика от нескольких влияющих факторов.

В большинстве случаев для задач диагностики имеют значение не абсолютные величины параметров, а отклонение этих параметров от нормы. Поэтому, с учетом линейности системы уравнений, заданных выражением (3.22), его предпочтительнее переписать в виде

, (3.23)

где [DY] – вектор отклонений диагностических параметров (откликов); [DR] – вектор отклонений влияющих факторов.

Линейность модели позволяет представить отклонения в относительном виде, что является особенно удобным:

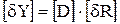. (3.24)

Вектор [dY] есть вектор относительных отклонений откликов (диагностических параметров), который задается своими компонентами d у_i. Вектор [dR] есть вектор относительных отклонений влияющих факторов, который задается своими компонентами d r_j.

Матрица [D] называется матрицей коэффициентов влияния. Каждая строка такой матрицы содержит коэффициенты, которые показывают во сколько раз (на сколько процентов) изменится данный отклик (выходной диагностический параметр) при изменении одного из возмущающих факторов на 1%.

Матрицу [D] удобно представлять в табличном виде (таблица 3.11). Такая таблица называется таблицей коэффициентов влияния и выглядит следующим образом. В заголовках столбцов указываются относительные отклонения влияющих факторов d r_j. В заголовках строк указываются относительные отклонения откликов (диагностических параметров) d y_i.

Таблица 3.11

Общий вид таблицы коэффициентов влияния

d уi \ d rj	d r 1		d ri		d rm
d у 1	d 11		d 1 j		d 1 m
d у 2	d 21		d 2 j		d 2 m
d у i	di 1		dij		dim
d уn	dn 1		dnj		dnm

 

В клетке, лежащей на пересечении i -й строки и j -гo столбца, записывается соответствующий коэффициент влияния d_ij, который показывает, на сколько процентов изменится i -й отклик при изменении j -гo влияющего фактора. Такая таблица похожа на таблицу состояния, однако в этой таблице размещены не нули или единицы, а коэффициенты влияния.

Использование таблицы коэффициентов влияния уже позволяет решать задачи определения технического состояния. Например, зная изменение откликов, оценить изменение влияющих факторов, которые непосредственно связаны с параметрами технического состояния.

На практике диагностические задачи чаще всего формулируются следующим образом: по известным измеренным значениям диагностических параметров (откликов) у_i определить техническое состояние (поставить диагноз). Если считать, что влияющий фактор r_j, определяет какую-либо неисправность, а все отклики (диагностические параметры) могут быть измерены, то предыдущее выражение (3.24) может быть представлено в виде, позволяющем напрямую решать сформулированную выше задачу:

. (3.25)

Матрица [D]^–1 является обратной для матрицы коэффициентов влияния [D] и называется диагностической. Диагностическую матрицу также можно представить в виде таблицы, где заголовками столбцов являются отклонения измеряемых параметров d y_i, а заголовками строк – диагнозы технического состояния, определенные отклонениями влияющих факторов d r_j. Данная таблица также похожа на таблицу состояний, и ее можно использовать для решения задач диагностики.

Отметим также, что в этом классе моделей могут использоваться алгебраические выражения, в которых несколько откликов связаны с несколькими факторами, и они не разрешены относительно откликов, например, следующего вида:

[C][dY] = [A][dR],

где [С] и [А] – матрицы коэффициентов влияния, соответственно, для откликов и для влияющих факторов. Эту систему уравнений можно решать путем последовательной подстановки или в матричном виде:

[dY] = [C]^–1 [A][dR].

Сделав подстановку [D] = [С]^–1[А], получим выражение, соответствующее формуле (3.24). Таким образом, соответствующими преобразованиями и в этом случае можно получить искомую матрицу коэффициентов влияния или диагностическую матрицу.

Мы рассмотрели случай представления модели в виде системы линейных алгебраических уравнений. Однако модель может быть представлена в виде системы нелинейных алгебраических уравнений. Если первоначальные алгебраические уравнения, описывающие объект, представлены в нелинейном виде, необходимо произвести их линеаризацию. Линеаризацию проводят в зависимости от вида нелинейности функции. Ниже рассмотрим несколько наиболее часто встречающихся вариантов.

1. Пусть алгебраическое уравнение, связывающее отклик у с факторами r_j,имеет вид

, (3.26)

т.е. в виде произведения функций.

При задании функции в таком виде для линеаризации проводится сначала логарифмирование, а затем дифференцирование исходного выражения.

После логарифмирования выражения (3.26) получим следующее уравнение:

.

После дифференцирования получим

Каждый член в правой части уравнения умножим и разделим на абсолютное значение соответствующего влияющего фактора. Например, первый член будет иметь вид