Диагностический вес признака

 

Последний вывод о том, что данные соотношения справедливы как для случая измерения комплекса признаков, так и для случая измерения отдельного диагностического признака или параметра, является весьма существенным. На его основе вводится ряд важнейших для практики понятий. Одним из таких понятий является диагностический вес признака.

В технической диагностике понятие диагностического веса признака вводится как величина, которая определяется следующим выражением:

. (4.12)

Данное выражение является эквивалентом количества информации, которое мы получаем о состоянии A_i после измерения признака k_j.

Рассмотрим некоторые свойства диагностического веса признака.

1. Если вероятность появления состояния А_i после измерения признака k_j больше вероятности появления этого состояния без измерения признака (т.е. P (A_i / k_j) > Р (А_i)), тогда Z_Aj (k_j) > 0.

2. Если условная вероятность появления состояния А_i равна обычной вероятности (т.е. P (A_i / k_j) = P (A_i)), тогда Z_Ai (k_j) = 0. Такая ситуация означает, что появление состояния А_i и появление признака k_j являются независимыми событиями.

3. Если условная вероятность появления состояния А_i меньше обычной вероятности (т.е. P (A_i / k_j) < Р (А_i), тогда Z_Ai (k_j) < 0. Такая ситуация свидетельствует о том, что появление признака k_j есть отрицание появления состояния A_i.

Учитывая предыдущие выражения (4.9) и (4.10), диагностический вес можно записать следующим образом:

(4.13)

или

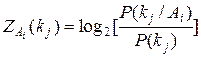. (4.14)

Определяемые этими соотношениями диагностические веса признаков называются независимыми (безусловными) диагностическими весами. При определении диагностических весов признаков по этим соотношениям предполагается ситуация, в которой обследование по признаку k_j не зависит от обследования по другим признакам.

Если производится обследование объекта диагностики по двум признакам k ₁ и k ₂ последовательно друг за другом и результаты обследования по k ₂ зависят от результатов обследования по k ₁, то вводится понятие условного диагностического веса.

Пусть в процессе диагностического обследования провели сначала оценку признака k ₁ и получили его реализацию k _{l s} . После этого провели оценку признака k ₂ и получили его реализацию k _{2 j}. Под условным диагностическим весом j -й реализации признака k ₂ понимается величина, определяемая следующим выражением:

, (4.15)

где P (k _{2 j} / A_i, k _{1 s}) является условной вероятностью появления (реализации) признака k _{2 j} при условии, что произошло событие, заключающееся в совместном появлении диагноза A_i и s -й реализации первого признака (т.е. k _{1 s}); P (k _{2 j} / k _{1 s}) – условная вероятность появления j -й реализации второго признака k _{2 j} при условии, что вначале была получена s -я реализация первого признака k _{1 s}.

Величина, определенная соотношением (4.15), показывает количество информации, получаемое о состоянии A_i по j -й реализации второго признака k _{2 j} при условии, что до этого уже была получена s -я реализация первого признака k _{1 s}. При этом диагностический вес признака k ₁ определяется по одной из вышеприведенных формул – (4.12), (4.13), (4.14), т.к. оценка этого признака производится в начале диагностического процесса и его значение не зависит от результатов оценки других признаков.

При необходимости определить количество информации, которая получается в результате двух последовательных исследований по признакам k ₁ и k ₂, вводится понятие суммарного диагностического веса:

. (4.16)

Эта величина показывает количество информации, получаемой о состоянии А_i при последовательном обследовании по признакам k ₁ и k ₂ и получении при этом соответственно реализаций этих признаков k _{1 s} и k _{2 j}.

Для практики диагностики бывает важно оценить информативность диагностического признака, имеющего несколько разрядов. Количество информации о диагнозе (состоянии) А_i, получаемое при обследовании по всем реализациям признака k_j, имеющего m разрядов, называется диагностической ценностью обследования по признаку . Эта диагностическая ценность обследования С_Аi () определяется следующим выражением:

(4.17)

где k_js – значение признака k^m_j, которое он приобретает при попадании в s -й разряд; (k_jS) – диагностический вес признака k_j разряда s для состояния A_i; P (k_jS / A_i) – условная вероятность появления k_j признака в разряде s для состояния А_i.

Диагностическую ценность обследования по m -разрядному признаку можно использовать:

1) для оценки эффективности применения при диагностировании выбранного диагностического m -разрядного признака.

2) для оптимизации числа разрядов признака проиллюстрируем последний вывод на примере.

Пусть имеется некоторый диагностический параметр у, который может изменяться от нуля до единицы, т.е. 0 £ у £1. Обследование большого числа объектов показало, что все значения у в данном диапазоне равновероятны, но для объектов с диагнозом А ₁ они лежат в пределах от 0,5 до 0,75. Требуется определить оптимальное количество интервалов, при котором обследование по данному признаку давало бы максимум информации, т.е. признак будет обладать максимальной диагностической ценностью.

Рассмотрим несколько вариантов разбиения интервала 0 £ у £1.

1. Разобьем этот интервал на два разряда: 0 – 0,5 и 0,5 – 1 и сформируем диагностический признак k ₁. Примем, что этот признак принимает значение k ₁₁ при попадании параметра у в первый интервал, т.е. при 0 £ у £0,5, или значение k ₁₂ при попадании параметра у во второй интервал, т.е.
при 0,5 £ у £ 1.Сучетом изложенного выше вероятности появления этих значений признаков (безотносительно к диагнозу) равны: P (k ₁₁) = P (k ₁₂) = 0,5. В то же время вероятности появления этих признаков при нахождении объекта в состоянии А ₁ различны, а именно P (k ₁₁ / A ₁) = 0 и P (k ₁₂ / A ₁) = 1.

В соответствии с формулой (4.17) диагностическую ценность двухразрядного признака k ₁ вычислим следующим образом:

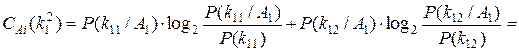
2. Разобьем интервал изменения диагностического параметра у на четыре разряда: 0…0,25; 0,25...0,5; 0,5...0,75; 0,75...1. Будем считать, что при попадании параметра в указанные разряды признак k ₁ принимает, соответственно, значения k ₁₁, k ₁₂, k ₁₃, k ₁₄. Как и в предыдущем случае, вероятности появления этих значений безотносительно к диагнозу равны между собой, т.е. P (k ₁₁) = P (k ₁₂) = P (k ₁₃) = P (k ₁₄) = 0,25. Условные вероятности появления указанных значений признака k ₁ при нахождении объекта в диагнозе А ₁ равны: P (k ₁₁ / А ₁) = 0, P (k ₁₂ / А ₁) = 0 и P (k ₁₄ / А ₁) = 0, а P (k ₁₃ / А ₁) = 1. Воспользуемся соотношением (4.17) для определения диагностической ценности обследования по четырехразрядному признаку k ₁:

Очевидно, что в этом выражении из четырех слагаемых только одно с Р (k ₁₃ / A ₁) = 1 не будет равно нулю. Таким образом,

.

3. Если произвести увеличение разрядности признака до восьми и выполнить аналогичные рассуждения, то вычисленное значение диагностической ценности обследования по полученному восьмиразрядному признаку также будет равно двум: .

Рассмотренный пример позволяет сделать очень важный вывод.

С увеличением числа разрядов диагностическая ценность обследования по заданному признаку будет возрастать и достигнет максимума. При дальнейшем увеличении разрядности величина диагностической ценности не будет меняться, а трудоемкость обследования будет увеличиваться.

Подводя итог данного раздела, отметим, что основные положения, изложенные в нем, являются весьма важными при разработке методов и средств диагностики и их следует использовать при формировании диагностических признаков и выборе их разрядности.

На конечном этапе диагностическая задача сводится к необходимости применения формализованных методов распознавания (классификации) диагнозов, основанных на математической обработке числовых данных, полученных в процессе измерения диагностических признаков или параметров. Эти методы в технической диагностике получили название «методы распознавания (разделения, классификации) диагнозов». Ниже рассмотрены некоторые подобные методы, наиболее часто используемые на практике.

 

4.5 Контрольные вопросы к главе 4

 

1. Чем определяется диагностическая ценность признака?

2. Чему равна энтропия системы в целом?

3. Чему равно количество информации о состоянии системы, полученное по результатам измерения?

4. Когда вводится понятие условного диагностического веса?

5. Как изменяется диагностическая ценность обследования по заданному признаку с увеличением числа разрядов?

ГЛАВА 5 МЕТОДЫ РАСПОЗНАВАНИЯ
В ТЕХНИЧЕСКОЙ ДИАГНОСТИКЕ

Основные понятия

 

В общем случае задача распознавания диагнозов формулируется следующим образом [2, 3, 11, 17].

Технический объект (система) может находиться в n состояниях, т.е. для этого объекта может наблюдаться совокупность диагнозов
D = (D ₁, D ₂,..., D_i,..., D_n), где i = l... n.

Каждое техническое состояние (диагноз D_i) описывается комплексом признаков К = (K ₁, K ₂, …, K_j,..., K_L), где j = 1... L. Каждый j -й признак обладает m_j разрядами.

Требуется построить решающее правило, с помощью которого объект, предъявленный для диагностики технического состояния, по полученному комплексу m_j -разрядных признаков мог быть отнесен к одному из возможных диагнозов D_i.

Для наглядности описания задач распознавания диагнозов удобно дать им геометрическую интерпретацию. При этом учтем, что в зависимости от свойств объекта диагностики, законов изменения параметров технического состояния, законов изменения диагностических параметров и, следовательно, диагностических признаков существуют два подхода к решению задач распознавания диагнозов: детерминистский и вероятностный.

Детерминистский подход имеет место в том случае, если каждый диагноз может быть описан конкретным набором диагностических признаков, которые принимают строго определенные значения. При этом данный набор значений признаков имеет место только для данного диагноза. С детерминистскими методами мы уже сталкивались на примере составления таблицы состояния.

Дадим геометрическую интерпретацию задачам распознавания диагнозов для детерминистского подхода. Пусть в результате оценки технического состояния определены конкретные значения диагностических признаков, т.е. получено, что объект диагностирования характеризуется комплексом признаков К = (К ₁, К ₂,..., K_j,..., K_l). Пусть признак K_j определяет значение j -й координаты некоторого вектора в L -мерном пространстве. Тогда набор признаков (К ₁, К ₂,..., K_j,..., K_l) определяет вектор, соединяющий начало координат и точку с соответствующими координатами в L -мерном пространстве. При таком представлении каждому диагнозу будет соответствовать строго определенная точка в L -мерном пространстве признаков. Предыдущие рассуждения будут справедливы и для случая, если в качестве координат L -мерного пространства использовать понятие «диагностический параметр». Поэтому описания диагнозов в L -мерном пространстве диагностических признаков или диагностических параметров эквивалентны.

Отметим, что поскольку практически значения параметров получаются с учетом погрешностей измерений, то для каждого диагноза, как в пространстве параметров, так и в пространстве признаков, мы будем иметь не точку, а некоторую область. Но главной особенностью детерминистской постановки задачи является то, что области различных диагнозов не пересекаются. Например, на рисунке 5.1 изображен случай (сплошные линии), когда объект диагностики может находиться в двух диагнозах D ₁ и D ₂, а его техническое состояние описывается двумя признаками (параметрами) К ₁ и К ₂.

 

Рис. 5.1 Представление областей диагнозов в пространстве признаков

 

Таким образом, при детерминистском подходе задача разработки решающего правила сводится к разделению пространства признаков (или параметров) на области диагнозов.

При детерминистском подходе для описания постановки диагностической задачи можно воспользоваться понятиями теории вероятностей. В случае перехода к понятиям теории вероятностей трактовка будет следующей. Если мы имеем набор признаков, принявших определенное значение, то вероятность диагноза, в область которого попала точка, определенная этим набором признаков, равна единице.

Такая трактовка предполагает, что каждый признак принимает конкретное значение только при одном диагнозе. При других диагнозах он принимает другое значение.

К сожалению, детерминистская постановка диагностической задачи зачастую невозможна, т.к. на диагностические параметры (а следовательно, и на сформированные на их основе диагностические признаки) воздействует огромное количество случайных факторов (изготовление элементов систем в пределах допусков, внешние условия работы, точность измерения и т.п.). В результате диагностические признаки (параметры) имеют существенный разброс значений даже для случая, когда объекты находятся в одном и том же диагнозе. Поскольку диагностический признак обладает существенным разбросом, то он становится величиной, которая только с некоторой вероятностью определяет появление конкретного диагноза.

В такой ситуации используется вероятностный подход к решению задач технической диагностики. При использовании вероятностных методов постановка задач распознавания диагнозов формулируется следующим образом.

1. Имеется технический объект, который может находиться в одном из n диагнозов D = (D ₁, D ₂,..., D_i,..., D_n). Появление конкретного диагноза D_i в данный момент времени случайно и определяется соответствующей вероятностью P (D_i).

2. Известна совокупность признаков К = (К ₁, К ₂,..., K_j,..., K_L), каждый из которых является случайной величиной, и возможность его появления характеризуется вероятностью Р (К_j).

3. Требуется сформулировать правило, с помощью которого можно по заданному комплексу признаков отнести объект к одному из диагнозов. То есть определить вероятность нахождения объекта в i -м диагнозе (появления события D_i) при условии, что экспериментально получен конкретный набор значений признаков К * = (, ,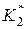..., ,..., ), где – конкретная реализация случайной величины K_j.

В геометрической интерпретации ситуация, соответствующая вероятностному подходу означает, что области диагнозов пересекаются, как это показано на рисунке 5.1 пунктирной линией для диагноза D ₁.

Вероятностные методы распознавания являются более общими. Поэтому ниже подробно рассмотрены наиболее широко используемые методы, относящиеся к этому классу.

Метод Байеса

 

Томас Байес (1702–1761) – английский священнослужитель и математик. Фундаментальные исследования в области теории вероятности изложены в «Эссе о решении проблем в теории случайных событий». Для практического применения формулы Байеса требуется огромное количество вычислений, поэтому расчет байесовских методов совпал с компьютерной революцией.

Процесс распознавания основан на сопоставлении признаков характеристик исследуемого объекта с признаками характеристик других известных объектов, в результате чего делается вывод о наиболее правдоподобном их соответствии. То есть этот метод основан на вычислении условной вероятности появления такого события, как диагноз D_i, при появлении конкретной реализации комплекса признаков К * [2, 3, 10].

Рассмотрим первоначально основные положения этого метода на простейшем случае, когда имеется диагноз D_i и один бинарный признак K_j, встречающийся при появлении этого диагноза.

Определим некоторые понятия:

1. P (D_i) – априорная (доопытная) вероятность появления диагноза D_i. Эту вероятность определяют по статистическим данным на начальном этапе применения метода, исходя из следующих соображений. Если при обследовании N объектов диагноза установлено, что из них N_i имеют диагноз D_i, то вероятность появления этого диагноза определяется соотношением

.

2. P (K_j / D_i) – априорная условная вероятность появления признака K_j у объектов, имеющих техническое состояние (диагноз) D_i. Эта вероятность также определяется на начальном этапе по имеющимся статистическим данным. Если из N обследованных объектов N_i, находилось в диагнозе D_i, а из них N_ij объектов имели признак K_j, то условная вероятность появления признака К_j, у объектов с диагнозом D_i вычисляется следующим образом:

.

3. P (K_j) – априорная условная вероятность появления признака K_j у всех объектов независимо от их состояния. То есть если из N объектов независимо от их технического состояния у N_j был обнаружен признак K_j, то эта вероятность определяется следующим образом:

.

Для случая, когда при постановке диагноза используется один простой признак, формула Байеса будет иметь вид

. (5.1)

Для принятия решения о диагнозе при использовании набора (комплекса) признаков применяется обобщенная формула Байеса, которую можно получить из следующих соображений. Если диагностирование проводится по комплексу признаков, то в результате обследования мы получаем конкретную реализацию каждого j -го признака К * _j и, следовательно, конкретную реализацию комплекса признаков К * в целом. В этом случае формула Байеса предстанет в виде

(5.2)

где Р (D_i / K *) – условная вероятность нахождения объекта диагностики в диагнозе D_i при условии, что в ходе обследования была получена конкретная реализация К * комплекса признаков К; Р (К *) – вероятность появления конкретной реализации К * комплекса признаков К у всех диагностируемых объектов, независимо от их технического состояния; Р (К * / D_i) – условная вероятность появления конкретной реализации К * комплекса диагностических признаков К для объектов, находящихся в диагнозе D_i.

Следует отметить, что метод Байеса обладает рядом недостатков:

1. Для реализации данного метода необходим большой объем экспериментальных начальных данных, которые можно получить только из результатов эксплуатации.

2. Для метода характерны большие погрешности при распознавании редких диагнозов из-за грубости оценок вероятности появления этих диагнозов.

3. Отсутствует однозначный критерий для выбора порогового значения вероятности Р (D_i / K * _s), по которому принимается решение по диагнозу.

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: