 |
Шестнадцать шишек. Классики. Грузим корабль. Высшая математика. Элементарно, Ватсон!
|
|
|
|
Шестнадцать шишек
Перед ведущим станции на столе шестнадцать шишек (или любых других предметов) Комиссар и вызвавшийся доброволец – Компьютер, играют в широко известную игру: можно по очереди забирать из кучки одну, две или три шишки. Проигрывает тот, кому достанется последняя.
Первым всегда делает ход ребенок, ибо комиссару хорошо известен алгоритм этой игры: десятая шишка должна быть твоя, а перед ней – шестая, а перед шестой – вторая. (Т. е. если ребенок случайно взял вторую, то у комиссара есть шанс завладеть шестой, а если и шестая мимо, то надежда на десятую все еще остается. )
Изначально на кону 70 сантиметров. За каждую проигранную партию из этой суммы вычитаются все те же 5 сантиметров. Игра продолжается до тех пор, пока Компьютер не выиграет. Дело в том, что если ребенок умный, то уже после второй-третьей партии он начинает нащупывать алгоритм и вскоре выигрывает. Ну а если неумный, то вполне возможно, что его правую ладонь украсит цифра «ноль».
Классики
Комиссар предлагает одному из подошедших вспомнить детство, т. е. игру в классики. На асфальте рисуется примерно вот такой рисуночек. (Или опять же совершенно, совершенно другой)
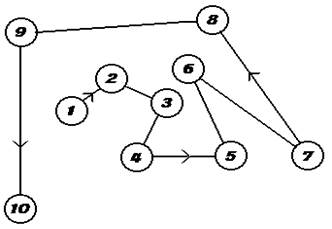
Комиссар с пристрастием допрашивает детей: кто, мол, из них лучше всех играл в пору своей далекой юности в классики?
Круглая железная коробочка из-под леденцов (или предмет, её заменяющий) бросается в круг (каждый круг в диаметре сантиметров шестьдесят), и нужно ногой, как в игре в классики, перемещать коробочку из круга в круг, зарабатывая по 5 сантиметров в каждом. Если коробочка касается черты, то 5 сантиметров в данном круге не засчитываются. Если она выходит за пределы круга, то все заканчивается.
|
|
|
Прежде чем приступить к зарабатыванию вожделенных сантиметров, девочка, которая на это вызовется (вряд ли это будет мальчик), имеет право один раз пройти этот путь тренировочно.
Грузим корабль
Комиссар вызывает Грузчика-добровольца и предлагает ему не более чем за пять секунд загрузить корабль чем-нибудь на букву «К». Каждые пять секунд нужно начинать грузить чем-нибудь другим. Например: коврами, контейнерами, кондиционерами, кастрюлями, канделябрами, компостерами, курами, контрамарками, кушаньями, контрабасами, карамелью и т. д.
Если по прошествии пяти секунд Грузчик не придумал, чем еще можно грузить корабль, то на этом – стоп. За каждый погруженный товар полагается оплата в размере 2 сантиметров. Самый сообразительный Грузчик назовет от силы два десятка слов.
Не советую грузить корабль на буквы «Э» или «Ц».
Высшая математика
Ведущий вручает вызвавшемуся Математику мел и школьную доску (роль которой с успехом может сыграть все тот же асфальт) «Сейчас я прочитаю условие простенькой задачки, которую тебе нужно решить. У тебя изначально 70 сантиметров. Пока ты решаешь задачку, я буду каждые двадцать секунд отнимать от них по пять сантиметров до тех пор, пока ты мне не скажешь правильный ответ. А теперь внимательно выслушай условие задачки: человек выпивает кадку вина за 16 дней. Вместе с женою – за 10 дней. За сколько выпьет кадку вина жена его? Время пошло! »
Здесь все понятно. Понятно и то, что каждый вожатый может найти и придумать целую кучу задач поинтереснее приведенной.
Элементарно, Ватсон!
На этой станции должен поработать тот, кто считает себя учеником Шерлока Холмса, одним из многочисленных достоинств которого была исключительная наблюдательность.
Комиссар заявляет подошедшему отряду: «Я – доктор Ватсон, и задам вам, мистер Холмс, десять наивных вопросов на наблюдательность. За каждый правильный ответ вы получаете 5 сантиметров. Прежде чем ответить, подумайте, а потом скажите: «Это же элементарно, Ватсон! »
|
|
|
И комиссар начинает задавать заранее подготовленные вопросы, подглядывая в шпаргалку. Вопросы должны быть о том, что дети видели и слышали много, много раз. Но обращали ли внимание? Это может относиться как к родному городу, так и к комиссарам, территории лагеря.
Например:
а) Прошу вас на секундочку отвернуться… Спасибо. А теперь, не скажете ли вы мне, мистер Холмс, во что обут зайчик, нарисованный у меня на куртке?
б) сегодняшнее дело ЗОЛОТОЙ ВОВОЧКА вела комиссар Оля. Были ли на ней серьги?
в) какого цвета скатерти у нас в столовой?
г) что за мелодия звучала сегодня по радиоузлу во время умывания?
д) сколько деревьев растет возле скульптуры пионера с веслом?
е) в нашем любимом городе есть памятник Петру Великому. Правой или левой рукой он держится за якорь?
ж) сколько колонн у нашего оперного театра?
з) какой породы собака постоянно дежурит возле кухни?
и) приличное или неприличное слово написано мелом на душевой?
Финальная стадия, или непосредственно БОЛЬШОЙ ПРЫЖОК
Все станции пройдены. Отряды очень стараются ровно в 18. 10 собраться на большой асфальтированной дорожке, на которой уже проведена нулевая черта. Руки у детей, как вы помните, исписаны цифрами и автографами комиссаров.
К этой самой нулевой черте подходит по одному ребенку от каждого отряда. Комиссары смотрят, сколько сантиметров заработал этот ребенок на предыдущем этапе и отмеряют от нулевой черты это же количество. Ребенок становится пятками на свою отметку и совершает прыжок с места. В той точке, куда приземлились его пятки, делается новая отметка, к которой подходит второй ребенок, и весь вышеописанный процесс начинается сначала.
Для зрелищности и интриги нужно, чтобы прыжки делались, не так, чтобы сначала отпрыгался первый отряд, за ним второй… По очереди, так интереснее.
Таким образом, в данном мероприятии побеждает тот отряд, который дальше прыгнет. За первое, второе и третье места вручаются ценные призы. Хорошо бы сделать это торжественно, с восхождением на пьедестал почета и с оркестром.
|
|
|
Хочу напомнить, что ценность данного дела в том, что здесь снова каждый ребенок вносит свой скромный вклад в результат отряда. Причем делает это дважды: первый раз – когда думает, второй – когда прыгает.
Для улучшения наглядности предварительного этапа можно, например, не писать цифры на детских ладонях (но расписываться обязательно), а вручать отрядам кусочек веревки той длины, которая заработана. Отрезки связываются. Два парня берут получившуюся длинную веревку за концы и так носят от станции к станции. Встречающимся на пути соперникам они эту веревку с гордостью или стыдливо демонстрируют, тогда сразу видно, кто впереди перед прыжком…
Победивший отряд ликует и как никогда чувствует свое единение. А отряды проигравшие полны досады на несправедливое судейство (любое судейство несправедливое) и тоже чувствуют единение как никогда.
В настоящий момент, когда я готовлю эту книжку к третьему переизданию, то рву на себе волосы от элементарной мысли, которая не пришла мне в голову раньше. Она пришла только на осеннем «Зеленом гусе». Конечно, конечно же – не должны отряды соревноваться с комиссарами. Отряды должны встречаться друг с другом. Стоит комиссар на игровом поле. Подходят два отряда.
От каждого выделяется по Челубею и Пересвету, они и соревнуются между собой, а комиссар – арбитр. Выиграл Челубей – его отряду достаются сантиметры, проиграл – сантиметры отряду Пересвета. Отряд болеет за своего. Если, скажем, отрядов на сборе числом восемь, то каждый отряд встречается с каждым и, следовательно, играет семь игр. Таким образом, семь человек от отряда вносят интеллектуальный вклад в отрядную копилку, а остальные – физический, т. е. прыгают. Этот вариант лучше по многим причинам. Во-первых, эмоциональный накал гораздо выше; во-вторых, процесс сплочения идет вверх намного круче; в третьих, сам прыжок, когда прыгает не весь отряд, а только 4-5 человек, проходит намного динамичнее.
Попробовал сделать на студентах и понял, что теперь БОЛЬШОЙ ПРЫЖОК будет проходить только так и не иначе. Совсем, совсем другое дело. Но… Совершенно неожиданно возникла труднейшая проблема чисто математического свойства. Оказывается, составить график встреч отрядов таким образом, чтобы ни одна пара отрядов не встретилась дважды, и ни разу один отряд не сыграл дважды в одну и ту же игру. Эта задача оказалась архисложная, и я на своём сайте обращался к вожатым, склонным к математике, с просьбой решить эту задачу.
|
|
|
Мне присылали решения, но всё они в итоге содержали ошибку. Так родилась вторая теорема Ферма. Красивого решения нет. Так что пришлось заряжать на шесть отрядов не пять, а восемь игр и некоторым отрядам просто стоять и ждать.
Или ещё проще. Встречаются четыре пары отрядов, и на всех четырёх площадках идёт одна и та же игра. Не очень удобно, но с математикой не поспоришь. Вот график встреч:
| Пенальти | Штурман | ОЗУ | Шестнадцать шишек | Классики | Грузим корабль | Элементарно, Ватсон |
| 1-2 | 1-3 | 1-4 | 1-5 | 1-6 | 1-7 | 1-8 |
| 3-7 | 2-8 | 5-7 | 2-4 | 2-5 | 2-6 | 2-7 |
| 5-8 | 4-7 | 3-2 | 3-8 | 3-4 | 3-5 | 3-6 |
| 6-4 | 6-5 | 8-6 | 6-7 | 7-8 | 4-8 | 4-5 |
Но БОЛЬШОЙ ПРЫЖОК – это уже далекое прошлое. Пора снова разойтись по отрядным местам для РАЗУЧИВАНИЯ ПЕСЕН с последующей СПЕВКОЙ.
 |
Большой прыжок. «Зелёный гусь»

|
|
|


