Объектный принцип моделирования
Как правило, алгоритмы, спроектированные по первым трем принципам, плохо модернизируются. А производственная ситуация часто меняется и требует соответствующих моделей для нахождения рациональных решений в процессе управления.
Таким образом, возникла необходимость в приемах моделирования, обеспечивающих независимость составления моделей элементов сложной системы от изменения задачи или структуры производства. Такой подход моделирования отдельных объектов независимо друг от друга позволяет собирать сколь угодно сложные системы без изменения их составляющих. Принцип объектного моделирования обеспечивает модернизацию сложных систем, удлиняя жизненный цикл АСУ.
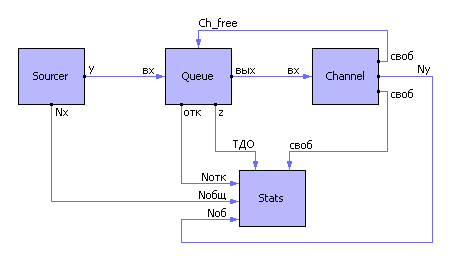
Пример. СМО состоит из следующих элементов, существующих самих по себе: источник заявок, очередь, канал (см. рис. 36.7). Смоделируем их по отдельности.
|
| Рис. 32.7. Схема реализации объектно-ориентированного моделирования (на примере СМО)
|
1. Источник заявок (Sourcer) генерирует последовательность случайных событий.
| // если счетчик x равен 0, то это момент появления заявки // tau — обеспечивает генерацию времени между заявками в момент появления заявки tau:= –1/λ · ln(rnd) · delta(x) + tau · not(delta(x)) // y — фиксирует факт появления заявки y:= delta(x) // счетчик моделирует заявочный процесс во времени, отсчитывая время между заявками // если счетчик x равен 0, то это момент появления заявки // если x больше нуля, то новая заявка пока не появилась x:= x + ed(~tau – x) · dt – x · ed(x – ~tau) // счетчик заявок Nx:= Nx + delta(~x)
| | |
2. Канал обслуживания (Channel).
| // канал свободен, если не обрабатывает заявку своб:= not(обраб) // своб — флаг-признак, если канал свободен, то «своб» равен 1. // обраб — флаг-признак, если канал занят, то «обраб» равен 1. // Если канал был свободен, и пришла заявка, то канал начинает ее обрабатывать. обраб:= ed(~своб · вх + not(delta(y)) // вх — сигнал о подаче заявки на обслуживание в канале // tau — обеспечивает генерацию необходимого времени обслуживания заявки в момент ее появления // Новая генерация происходит только в том случае, если канал свободен и пришла заявка // Если в канале обслуживается заявка, то новое tau не генерируется // mu — интенсивность потока обслуживания (задается константой) tau:= –1/mu · ln(rnd) · ~своб · ~вх + tau · not(delta(~y)) своб: = not(~обраб) // счетчик «y» моделирует заявочный процесс во времени, отсчитывая время обслуживания // если «y» выдал 1, то значит канал выдал обслуженную заявку y:= y + ed(~tau – ~y) · dt – ~y · ed(~y – ~tau) // счетчик обслуженных заявок Ny:= Ny + delta(~y) // флаг «обработка» будет погашен, если закончится время обслуживания обраб:= not(delta(~y)) // канал будет свободен, если канал не обрабатывает заявки своб:= not(~обраб) // счетчик накапливает статистику — общее время простоя канала ОВП:= ОВП + ~своб · dt // счетчик накапливает статистику — общее время работы канала ОВР:= ОВР + ~обраб · dt
| | |
3. Очередь (Queue).
| // «отказ» — счетчик фиксирует отказ, если все места в очереди заняты (Z > Zm) // и приходит очередная заявка (вх = 1) // Zm — максимальное количество мест в очереди // Z — текущее количество занятых мест отказ:= ~отказ + delta(~вх – 1) · ed(~Z – Zm + 1) // счетчик количества занятых мест в очереди увеличивается, если приходит // заявка и есть незанятые места в очереди Z:= Z + delta(~вх – 1) · ed(Zm – Z) // передаем заявку из очереди в канал // флаг, фиксирующий освобождение места в очереди в момент // освобождения канала, если очередь есть // ch_free — флаг (свободен (1) или занят канал обслуживания (0)) вых:= delta(~ch_free – 1) · ed(~Z) // счетчик уменьшает количество занятых мест в очереди, // после взятия заявки в канал обслуживания Z:= Z – ~вых
| | |
4. Статистика (Stats).
| Tэкс:= Tэкс + 1 · dt проп_сп:= Nоб/Tэкс Pоб:= Nоб/Nобщ Pотк:= Nотк/Nобщ Tпрост1:= Tпрост1 + ~своб1 · dt Tпрост12:= Tпрост12 + ~своб1 · ~своб2 · dt Tпрост123:= Tпрост123 + ~своб1 · ~своб2 · ~своб3 · dt ср_кол_пр_КО:= Tпрост1 + Tпрост12 · 2 + Tпрост123 · 3 ср_кол_зан_КО:= всего_КО – ср_кол_пр_КО S:= S + ~тек_дл_очер · dt ср_дл_очер:= ~S/Tэкс
| | |
Данные модели могут собираться в любые конфигурации без изменения их содержания.
Моделирование марковских случайных
процессов
Очень удобно описывать появление случайных событий в виде вероятностей переходов из одного состояния системы в другое, так как при этом считается, что, перейдя в одно из состояний, система не должна далее учитывать обстоятельства того, как она попала в это состояние.
Случайный процесс называется марковским процессом (или процессом без последействия), если для каждого момента времени t вероятность любого состояния системы в будущем зависит только от ее состояния в настоящем и не зависит от того, как система пришла в это состояние.
Итак, марковский процесс удобно задавать графом переходов из состояния в состояние. Мы рассмотрим два варианта описания марковских процессов — с дискретным и непрерывным временем.
В первом случае переход из одного состояния в другое происходит в заранее известные моменты времени — такты (1, 2, 3, 4, …). Переход осуществляется на каждом такте, то есть исследователя интересует только последовательность состояний, которую проходит случайный процесс в своем развитии, и не интересует, когда конкретно происходил каждый из переходов.
Во втором случае исследователя интересует и цепочка меняющих друг друга состояний, и моменты времени, в которые происходили такие переходы.
И еще. Если вероятность перехода не зависит от времени, то марковскую цепь называют однородной.
Воспользуйтесь поиском по сайту: